复杂截面扭转问题的孔洞拟填充法分析

赵兰磊，陈文家，何彦忠，李鹭扬＊，黄 鑫

（1.扬州大学机械工程学院，江苏扬州225127；2.江苏扬力集团精密机床研究所，江苏扬州225127）

复杂截面扭转问题的孔洞拟填充法分析

赵兰磊1，陈文家1，何彦忠2，李鹭扬1＊，黄 鑫1

（1.扬州大学机械工程学院，江苏扬州225127；2.江苏扬力集团精密机床研究所，江苏扬州225127）

为解决复杂截面应力、变形问题的求解，以柱体扭转问题的应力函数及多连域转化为单连域的方法为基础，应用有限元－边界元法，提出了“孔洞拟填充”的方法，并利用有限元分析软件ANSYS Workbench以偏心轮为例模拟求解扭转问题.结果证明该方法可以适用于任何截面的杆件.

复杂截面；应力函数；多连域；拟填充；有限元；扭转

在车辆以及机械设备中普遍使用承受扭矩载荷的部件（如偏心轮，偏心齿轮）及采用非圆截面（如矩形、三角形、椭圆形等）的轴，这些承扭件的横截面往往为复杂的多连域，对其扭转问题通常难以求得解析解，从而使其强度和刚度计算成为设计中的难点.目前处理复杂截面的扭转问题所采用的方法有变分解法、边界元法［1－3］、虚边界元法［4］、分离变量法［5］、复变函数法［6］、多连域转化为单连域法［7］、有限元法［8－9］等.如何借助计算机和现代分析手段分析承扭杆的结构问题，并精确求解这些扭杆件的应力、应变状态及抗扭刚度，具有一定的研究价值.本文以有限元－边界元法及多连域转化为单连域的方法为基础，基于虚单元、截面的拓扑优化［10］、轮廓的孔洞填充算法［11］、无网格有限元法［8］、间断有限元法［9］、任意复杂薄壁截面自由扭转常数的计算［12］、多单元扭转常数的分析［13］、任意截面形状的钢筋混凝土杆的扭转刚度［14］，分析多单体梁的扭转、变形和翘曲［15］，提出了“孔洞拟填充”的概念，应用“孔洞拟填充”思想来处理复杂截面的扭转问题.

图1 任意多连域截面Fig.1 Arbitrary multipleconnected cross sections

1 复杂截面扭转问题的理论以及实例分析

1.1 有限元－边界元法

根据弹性力学中在柱体周围侧面（曲面）上的应力关系及柱体扭转问题的性质，可以得出应力在边界上的关系式为τxzcos（n，x）＋τyzcos（n，y）＝0（n是侧面的外法线方向），也可以写成

由式（1）可得知应力函数在边界上一定是一个常数.对于一般情况下的多连域截面扭转问题，其图形如图1所示，则多连域截面的扭矩可以写为

式中G为剪切弹性模量；Φ为应力函数；θ为单位长度的扭转角.

对式（2）进行积分计算，并运用格林公式将面积的积分转化为沿曲线的积分，可以简化为

由式（1）已得知应力函数在边界上是一个常数，由于通常情况下取截面最外边界Γ0（截面外边界）上的应力函数Φ0＝0，而其他的内边界Γ1，…，Γn在每一边界上应力函数Φ都是常数，但这个常数不一定相等，故取此常数为k（待定的常数），即Φi＝ki，其中i＝1，2，3，…，n.假设S与截面内一个边界Γi重合，所以式（3）可以变为

按照应力函数求解多连域截面杆扭转问题的边界元法，可得边值问题的关系式

因为多连域截面内的应力分量为τxy，τyz，因此对应的普朗特应力函数为

由式（9）可以得到某一点处的应力τ为

由此可见，用边界元法求解多连域截面杆扭转问题，须将多连域截面的边值问题转化为在相同区域内同一离散格式下进行求解.首先解出Φ和θ，然后代入式（8），再与式（9）、（10）联合求解，即可确定多连域截面杆在扭矩作用下的应力问题.

依据上述方法，以偏心轮为例，借助于有限元－边界元法对其进行分析计算.已知：R1，R2，R3，R4；截面承受的扭矩为M；各点对应的位置坐标见图2.根据图2及其相关参数确定各坐标点之间的关系式和矩阵关系式，然后确定孔洞的面积，利用公式Ai＝Ωjdxdy对孔洞部分进行面积的求解，将所求面积及公式Φ＝代入式（7），可以算出待定常数ki，再回代到公式Φ＝，即可求得应力函数Φ的值；将所得Φ值和由式（2）所得单位长度的扭转角θ代入式（9），（10），可求得偏心轮某点的应力值.

图2 偏心轮Fig.2 The eccentric wheel

1.2 “孔洞拟填充”的思想

随着等值面数的增加以及区域Ω（截面域）形状的多变，结果的求解也将变得复杂起来，原因是由于多连域及其内部的边界条件存在，使得结果的求解处理难以进行.究竟采用什么方法才可以有效避免多连域和边界条件的影响？为此，考虑到有限单元法.因为其可以把计算域划分为有限个互不重叠的单元，在每个单元内选择一些合适的节点作为求解函数的插值点，从而把复杂问题简单化；但是将复杂截面划分成有限个小单元后，由于不同的小单元具有的材料性能可以不相同，那么能否将复杂截面中的孔洞进行填充，然后转变为单连域问题求解？据此出现了“孔洞拟填充”的思想，其实质性的原理是将截面内边界Γi所围成的孔洞部分视作由密度和剪切弹性模量极小的虚拟材料填充而成，然后对此部分虚拟域进行单元划分，再根据应力函数的连续性和位移单值条件，将多连域转化为单连域，即将运算转变为在外边界Γ0所围成的整个二维面域Ω0上进行求解计算.

根据应力函数理论，可知多连域截面扭转问题的控制方程（欧拉方程）和边界条件的一般形式为

其中由于是假设拟填充孔洞，而不同单元具有的材料特性可能不同，故将剪切弹性模量G看作是x，y的函数.当采用有限单元法时，将G在每个小单元内视为常数，孔洞区域的G可取有材料区域的10－10倍［7］159.若能求解出应力函数Φ，则再根据式（10）即可得出某一点的应力值τ0.为了便于Φ的计算，利用变分原理可以进行边值问题求解，故采用Galerkin法的等效积分从泛函方面进行分析求解，由此得到的多连域截面扭转问题的泛函表达式为

取式（13）的极值条件，由驻值条件δΠ（Φ）＝0可得到关系式

式中Ω0为截面外边界Γ0所包围的区域.由于有限元法实际上是Ritz法的推广，所以根据Ritz法，由公式δΠ（Φ）＝0可得到的近似解为

由式（15）可得单元矩阵关系式

式中n表示每个小单元节点个数；Φe表示单元的应力函数且满足强制性边界条件；Νi为试探函数（形函数）.

由公式δΠ（Φ）＝0也可以得出关系式Π＝（Π／Φ1）δΦ1＋（Π／Φ2）δΦ2＋…＋（Π／Φnl）.δΦnl＝0，其中Φ1，Φ2，…，Φn相互独立，由此可以确定每个小单元的应力函数Φi；所以，对每个小单元应用变分原理，利用式（15）和（16）以及Π／Φ＝0可以得到KΦ＝R，其中K表示整个截面的刚度矩阵，它的每一个单元的刚度矩阵都反映了一定的刚度特性，K＝∑eKe，Ke＝，其中Ge表示单元剪切弹性模量；R表示整个截面应力函数的列阵，R＝∑eRe，Re＝2θ∫Ω0NTΦ，其中Φ表示整个截面的节点应力函数的列阵.此时应力函数Φ可求出，将其代入式（10）即可求得某点的应力值.

用孔洞拟填充方法求解，相对于边界元法，求解偏心轮上某点的应力函数比较简单，其求解目的是将偏心轮转化为无孔洞的承扭杆件的截面.已知偏心轮的剪切弹性模量为G，将其上的孔洞用剪切弹性模量10－10G的材料进行填充，求解过程为：根据上述分析已知每个小单元的的应力函数Φi为常数，由于试探函数Νi事先给定，所以利用KΦ＝R，式（11）以及变分原理式可以求出应力函数Φ，将所得Φ代入式（12），可得到单位长度扭转角θ，然后将求解得到的Φ和θ代入式（9），（10），即可求解出偏心轮某点的应力值.

2 基于ANSYS Workbench的实例分析

采用Solidworks建立偏心轮三维模型，图3为一般的求解模型图，图4为虚拟填充模型图，并将其分别保存为Parasolid格式.将偏心轮的模型图导入到有限元分析软件ANSYS Workbench中，进行加载、约束、定义分析类型、分析选项、载荷数据和载荷选项等步骤，然后开始有限元求解，其中对图3采用有限元法求解，图4采用孔洞拟填充法求解.在进行分析求解时，偏心轮的材料选择碳素钢，2种情况下偏心轮所具有的基本参数（密度ρ、弹性横量E、泊松比μ，屈服应力σs、破坏应力σu）如表1所示.

表1 偏心轮基本参数Tab.1 Basic parameters of the eccentric with hole and dummy filling

对图3、图4两种情况下的偏心轮进行网格划分，其图形如图5～6所示.

图3 偏心轮的三维模型图Fig.3 The 3D model of the eccentric wheel

图4 孔洞拟填充偏心轮的三维模型图Fig.4 The 3Dmodel of the eccentric wheel with hole and dummy filling

图5 偏心轮网格Fig.5 Eccentric wheel grid

图6 孔洞拟填充偏心轮网格Fig.6 The grid of the eccentric wheel with hole and dummy filling

对以上偏心轮的模型加载求解，经求解处理后偏心轮在2种情况下所得到的应力、位移以及应变的分析结果如图7～10所示.

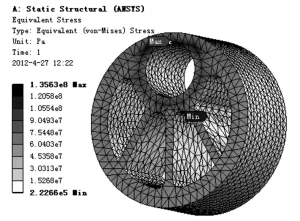
图7 应力云图Fig.7 Stress nephogram

图8 孔洞拟填充偏心轮的应力云图Fig.8 The stress nephogram of the eccentric with hole and dummy filling

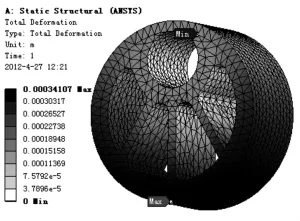
图9 位移云图Fig.9 Displacement nephogram

图10 孔洞拟填充偏心轮的位移云图Fig.10 The displacement nephogram of the eccentric wheel with hole and dummy filling

对偏心轮采用2种方法计算后所得数据见表2，求解后偏心轮的变形曲线和应力曲线如图11～12所示.

通过以上计算对所得云图以及表2的数据进行对比分析可知：偏心轮和孔洞拟填充偏心轮在2种工况下对应的应力曲线图和变形曲线图形状基本相同，最大应力值和最大变形值出现的位置相同，并且最大应力值都小于许用应力值142MPa，从而满足偏心轮本身所具有的强度要求.由此说明偏心轮在2种工况下的计算结果具有相似性.利用“孔洞拟填充”思想可以有效处理复杂截面扭转问题的应力值，求解其变形量，从而充分验证了本文方法的准确性.

表2 偏心轮的最大应力值和变形量Tab.2 Maximum stress value and deformation of the eccentric wheel

［1］ 欧贵宝.多连域截面杆扭转问题的边界元法［J］.哈尔滨船舶工程学院学报，1988，9（4）：469－475.

［2］ SAPOUNTZAKIS E J，TSIPIRAS V J.Composite bars of arbitrary cross section in nonlinear elastic nonuniform torsion by BEM［J］.J Eng Mech，2009，135（12）：1354－1367.

［3］ SAPOUNTZAKIS E J，DIKAROS I C.Non－linear flexural－torsional dynamic analysis of beams of arbitrary cross section by BEM［J］.Int J Nonlinear Mech，2011，46（5）：782－794.

［4］ 杨冬升，凌静.虚边界元多连通区域边界离散及边界条件分析［J］.佳木斯大学学报：自然科学版，2011，29（2）：161－163.

［5］ 程耀芳，赖远明，王云峰.任意截面形状直杆扭转问题的解析解［J］.兰州铁道学院学报，1998，17（2）：13－16.

［6］ 尹昌言.含多个纵向圆孔的圆轴的扭转［J］.东北重型机械学院学报，1989，13（3）：10－18.

［7］ 李永奇，张卫红.模拟求解任意截面杆扭转的化复为单有限元方法［J］.兰州理工大学学报，2006，32（2）：158－161.

［8］ IDELSOHN S R，ONATE E，CALVO N，et al.The meshless finite element method［J］.Int J Numer Methods Eng，2003，58（6）：893－912.

［9］ 康澜，张其林，王忠全，等.任意复杂薄壁截面自由扭转常数的数值计算方法［J］.中南大学学报：自然科学版，2011，42（5）：1437－1441.

［10］ KIM Y Y，KIM T S.Topology optimization of beam cross sections［J］.Int J Solids Struct，2000，37（3）：477－493.

［11］ 张德才，周春光，周强，等.基于轮廓的孔洞填充算法［J］.吉林大学学报：理学版，2011，49（1）：82－86.

［12］ HANSBO P，LARSON M G.Discontinuous Galerkin methods for incompressible and nearly incompressible elasticity by Nitsche’s method［J］.Comput Methods Appl Mech Eng，2002，191（17／18）：1895－1908.［13］ LUBARDA V A.On the torsion constant of multicell profiles and its maximization with respect to spar position［J］.Thin Wall Struct，2009，47（6／7）：798－806.

［14］ KIM J H，KIM Y Y.Thin－walled multicell beam analysis for coupled torsion，distortion，and warping deformations［J］.J Appl Mech，2001，68（2）：260－269.

［15］ LI Zhao－xia，KO J M，NI Y Q.Torsional rigidity of reinforced concrete bars with arbitrary sectional shape［J］.Finite Elem Anal Des，2000，35（4）：349－361.

图11 偏心轮的应力曲线Fig.11 Eccentric wheel stress curve

图12 偏心轮的变形曲线Fig.12 Eccentric wheel deformation curve

Abstract：By the finite element／boundary element method，on the base of torsion problems of the cylinder stress function and converting multiple－connected regions into simple－connected region method，this paper proposes a“hole and dummy filling”method to solve the problem of stress and strain of complicated section.Using eccentric wheel as an example，the problem of torsion is analyzed by ANSYS Workbench finite element software.The study proves that the method is applicable to bars with arbitrary cross－section.

Keywords：complicated section；stress function；multiple connected regions；dummy filling；finite element；torsion

（责任编辑 贾慧鸣）

Analysis of the complicated section torsional problem with“hole and dummy filling”method

ZHAO Lan－lei1，CHEN Wen－jia1，HE Yan－zhong2，LI Lu－yang1＊，HUANG Xin1
（1.Sch of Mech Engin，Yangzhou Univ，Yangzhou 225127，China；2.Precis Mach Tool Res Inst of Jiangsu Yangli Group，Yangzhou 225127，China）

TH 123.4

A

1007－824X（2012）02－0047－05

2012－01－12

扬州市－扬州大学科技合作基金（YZ2010154）

＊联系人，E－mail：meliluyang＠126.com