圆柱滚子轴承动静态有限元分析

王军领，郑 翔，吴 焕

（扬州大学机械工程学院，江苏扬州225127）

圆柱滚子轴承动静态有限元分析

王军领，郑 翔＊，吴 焕

（扬州大学机械工程学院，江苏扬州225127）

通过SOLIDWORKS三维软件对圆柱滚子轴承进行建模，并利用ANSYS有限元分析软件对圆柱滚子轴承进行合理的加载和求解，经过Block Lanczos方法的模态分析得到前6阶的固有频率、振型以及共振下的薄弱部位；经过加载极限动载荷值94kN下的静态分析得到工况下的最大应力值、变形值以及变形、应力的分布规律，对圆柱滚子轴承的刚度进行了校核，为轴承的结构优化提供建议和方法.

圆柱滚子轴承；振动；有限元分析；应力

随着科技与工业的发展，圆柱滚子轴承的应用越来越广泛.［1］通过轴承的失效形式可知圆柱滚子轴承在负荷运转时会发生许多接触或碰撞，且都与轴承的接触受力相关，是非线性变形问题［2］；因此，对圆柱滚子轴承的内、外圈及滚动体进行动静态分析具有十分重要的意义.KANG Yuan等［3］曾对接触有限元分析进行了实验验证.FILETTI［4］和CAVALLARO［5］等又分别对带有轴承外圈和柔性套圈的圆柱滚子轴承进行了性能分析.本文在前人理论分析的基础上，利用有限元分析软件对圆柱滚子轴承进行动静态综合分析，为轴承的选择和设计开发了新的途径.

1 有限元模型

基于圆柱滚子轴承的结构参数，本文在SOLIDWORKS标准件库中提取出相应的参数化三维模型，并确定材料的弹性模量为219GPa，泊松比为0.3，密度取7 830kg·m－3［6］，为有限元分析做好前期准备，轴承参数见表1.

表1 轴承参数Tab.1 Bearing parameters

在网格划分中，选取具有10节点四面体结构，既能保证精度，又允许存在不规则形状的单元类型Solid Tet 10node92.因其具有相容的位移形状，所以非常适用于曲线边界建模的结构.另外，Solid 92在每个节点都有沿节点坐标x，y，z3个方向的自由度，具有应力强化、大变形、大应变、塑性和蠕变的特性.［7］在网格划分的技术上本文采取自由划分，并利用智能尺寸控制技术自动控制网格的大小与疏密分布.因精度越高，计算时间越长，所以为了平衡计算时间和计算精度，笔者将智能划分精度设置为8，并加密接触部位的网格.

2 动力学分析

2.1 模态分析

模态分析主要用于确定结构或机器零部件的振动特性，即固有频率与振型.［8］设计轴承最关键的是降低其工作中的振动和噪声，所以模态分析在轴承设计中尤为重要.本文将圆柱滚子轴承外圈的外表面固定，并采用Block Lanczos方法对其进行有限元模态分析.由于阶数越高，频率越快，振动方式越复杂，误差也越大，而对实际应用有意义的仅为前几阶频率较小的固有频率，因此只须列出结构的前几阶固有频率和部分振型.

2.2 结果与讨论

模态分析可以在设计轴承结构中避免共振或其他形式的振动，直观地观察轴承结构在不同类型的动力载荷下如何振动和响应.圆柱滚子轴承的前6阶的固有频率和振型位移如表2所示.

表2 轴承各阶固有频率Tab.2 The natural frequencies of the bearing

由于振动使得轴承外圈与滚子、滚子与内圈、内圈与轴、外圈与轴承座的配合发生变化，特别是内、外圈与滚子的配合发生变化，从而加速了轴承损坏速度，降低了轴承使用寿命和传动精度的可靠性，影响轴承的使用性能.为了防止轴承结构发生共振，减少振动对轴承传动精度的影响，所以应避免外界振源的激励响应频率与轴承的固有频率相同或相近.若不能避免外界振动，则应考虑采取减振隔振措施，尽量减小外界振动对轴承性能的影响.由振动位移云图（如图1，2）可知，轴承外圈边缘是振动时位移最大的位置，在设计中该位置应重点加强.由于轴承是轴对称的，并通过振动动画可知1阶和2阶振动是相同的角向振动，3阶与4阶也是相同的复杂角向振动，5阶是轴向振动，故文中只列出前两阶固有振型.由于轴承的每阶固有频率很高，所以一般共振对轴承性能影响很小；而在高速运转和需要高精度传动的场合，振动对轴承的影响则很大，此时应重视圆柱滚子轴承的振动特性.

图1 第1阶振型Fig.1 First－order vibration mode

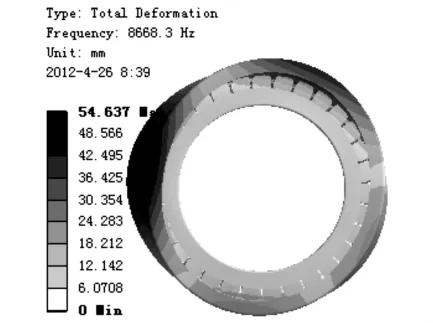
图2 第2阶振型Fig.2 Second－order vibration mode

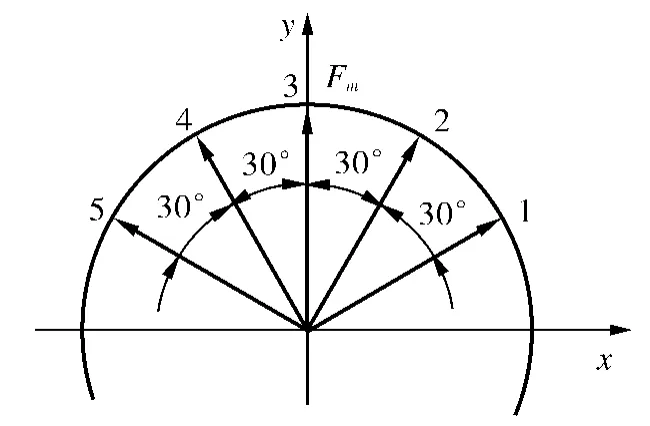
图3 受力分解示意图Fig.3 Force decomposition diagram

3 线性静力分析过程

3.1 约束条件和载荷施加

轴和轴承内圈属于过盈配合，接触表面在无变形时可以视为完全或接近完全贴合在一起，故可将压力在轴承内圈的分布表示为如下的余弦函数［9］：Fα＝Fmsinα，式中Fm为轴作用在轴承内圈上的最大载荷.将轴承内圈与轴之间接触力作用的接触表面平均分成6个部分（如图3图中矢量箭头为正弦力分量），可得到

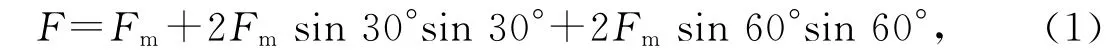
简化后得到Fm＝F／3.

根据轴承强度的校核公式C0≥S0·，由动载荷的极限值C0＝188kN可得轴承承受的最大动载荷F＝P0＝94kN，其中轴承静强度安全系数S0取值应大于1，此处取2.

轴承运转时一般内圈随轴转动，外圈静止，且固定于刚性很大的轴承座上，因此对外圈表面的6个自由度应完全施加为固定约束.在内圈外表面与每个滚子圆柱面之间，外圈内表面与每个滚子圆柱面之间建立接触面.［11］载荷压强加在内圈内表面上，方向垂直于接触面向外.由于轴作用在轴承内圈表面的接触力是方向不一致且大小不同的压强，所以将上面按正弦函数变化的压强加载在轴承内圈表面，如图4所示.此外，也可通过实体与实体接触的方法［12］对轴与轴承内圈进行接触分析.

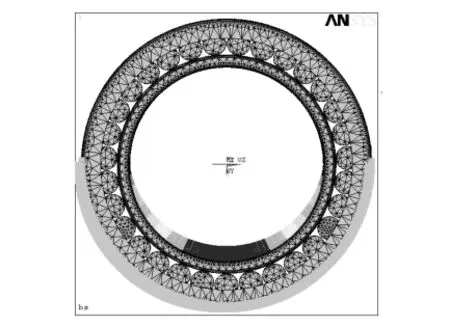
图4 正弦函数载荷图Fig.4 Loading diagram of sine function load

3.2 数据分析与讨论

经过计算可得总体等效位移云图如图5所示.由ANSYS分析结果可知，等效位移在x，y，z方向的分量最大值分别为2.9，11.2，4.3μm，合成后的最大等效位移为11.5μm.由于轴承的外圈固定，几乎无变形，故变形主要集中在轴承内圈与轴之间受挤压的接触位置，且最大值发生在轴承内圈的底端，整个结构的位移云图相对于y轴左右对称.根据轴承具体的使用场合和精度要求.在极限载荷下，本文结果可以接受且满足条件.

由轴承的等效应力云图（图6）可见，应力最大值发生在圆柱滚子与内、外圈接触之处，由于接触面积很小，应力值较大，导致应力集中，且等效应力云图和接触应力分布相对于y轴对称.应力最大值为245.43MPa，由于此分析对轴承加载的力是动载荷的极限载荷，除去应力集中现象造成的误差，此数值仍在轴承刚度和强度承受的范围内.若要增加轴承承受的应力值，则可对轴承的圆柱滚子及内、外圈表面进行热处理，如淬火处理，以减少磨损和应力集中.

轴承虽然简化成静态计算，但其性能分析应该从动态来考虑.在轴承工作时，外圈固定于轴承座，内圈固定于轴并随轴转动，轴承的内外圈和滚子所受的是周期性往复循环载荷，且所受应力和产生的变形呈周期性变化，即当内外圈和滚子进入接触承载区域后，接触力和产生的应力与变形从零开始逐渐增加到最大值后再减小为零，同时可知内外圈与滚子接触处每一点上的应力和变形也呈周期性变化.由图7的应力云图可知，受径向载荷下轴承的应力较大值大多发生在滚子与内外圈接触处，且在最底端的滚子与内外圈接触部位的应力值最大，而向两侧逐渐变小，说明滚子与内外圈接触处是应力相对集中的部位.因轴承上部未受压，故接触力主要集中于下部.由上述分析可知轴承制造时应采用抗压性能较强的材料，且经过本文方法计算所得的应力不得大于需用应力.由图7可见，在滚子与内外圈的接触区域出现了应力集中，即应力随着网格密度的增加而增大，而在实际应用中材料会产生一定的屈服和变形，接触面积不再是一条线，而是一个面，所以抗压强度会有所提高，但如果压力过大也会出现滚子被压溃或内外圈被点蚀的危险，这与实际应用情况相符.

图5 等效位移云图Fig.5 Equivalent displacement deformation

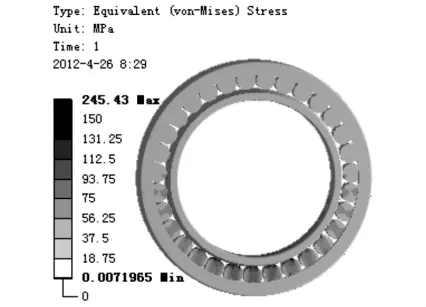
图6 等效应力云图Fig.6 Equivalent stress distribution

图7 圆柱滚子的应力云图Fig.7 Stress distribution of cylindrical roller

4 结论

1）由轴承模态分析可知其结构的前几阶固有频率和振型，为更深层次的动力学分析提供数据和参考，找出了轴承整体结构在共振下的薄弱部位.

2）轴与轴承之间接触表面的接触力并不是均布的，而是呈正弦函数变化的.本文为了更真实地模拟出轴对轴承内圈的载荷作用情况，利用函数编辑器编辑正弦函数，并在轴承的内圈圆中心建立局部圆柱坐标系，对其加载随正弦函数变化的接触力，可以得出更符合实际的结果.

3）利用ANSYS有限元分析软件可以直观地显示滚子轴承在受径向载荷作用下，轴承整体结构的变形值和应力值及其分布情况，为轴承的结构优化提供了建议和方法，简化了轴承的设计开发步骤，降低了强度校核的周期和成本.

［1］ 杜静，黄文，李成武，等.基于GAP单元的滚动轴承应力分析［J］.机械设计与制造，2011（6）：43－45.

［2］ ORLOV A V.Ball－bearing wear in real loading conditions［J］.Russ Eng Res，2009，29（9）：884－890.

［3］ KANG Yuan，SHEN Ping－chen，HUANG Chih－ching，et al.A modification of the Jones－Harris method for deep－groove ball bearings［J］.Tribol Int，2006，39（11）：1413－1420.

［4］ FILETTI E G，RUMBARGER J H.A general method for predicting the influence of structural support upon rolling element bearing performance［J］.ASME J Lubr Technol，1970，92（1）：121－182.

［5］ CAVALLARO G，NELIAS D，BON F.Analysis of high－speed intershaft cylindrical roller bearing with flexible rings［J］.Tribol Trans，2005，48（2）：154－164.

［6］ 张永奇，张清，谭庆昌.减速器圆锥滚动轴承有限元分析［J］.试验技术与试验机，2007（2）：8－10.

［7］ 马天兵.基于ANSYS的滚动轴承有限元分析［J］.煤矿机械，2004（2）：66－68.

［8］ GHAFARI S H，GOLNARAGHI F，ISMAIL F.Effect of localized faults on chaotic vibration of rolling element bearings［J］.Nonlinear Dyn，2008，53（4）：287－301.

［9］ 张祖芳.开式压力机机身的有限元分析及其优化设计［D］.南京：东南大学，2004.

［10］ LIU Xiu－hai，DENG Si－er，TENG Hong－fei.Dynamic stability analysis of cages in high－speed oil－Lubricated angular contact ball bearings［J］.J Trans Tianjin Univ，2011，17（1）：20－27.

［11］ 王兴东，董元龙，刘源泂.低速重载轴承的有限元分析及研究［J］.武汉科技大学学报：自然科学版，2008，31（1）：104－107.

［12］ 蒋波，赵毅红，王军领，等.基于ANSYS的提环有限元分析及优化［J］.扬州大学学报：自然科学版，2011，14（4）：60－63.

Abstract：This paper models a cylindrical roller bearings by SOLIDWORKS software and gives it a reasonable load and solution using ANSYS software.It also calculates the first six natural frequencies and mode shapes through Block Lanczos method of modal analysis，identifies the weak parts of bearings under the natural frequencies.The maximum stress and deformation values as well as the distribution of deformation and stress are obtained after the limit dynamic load value 94kN static analysis.The stiffness of the cylindrical roller bearings is checked.Some suggestions and methods to optimize the structure of the bearing are provided.

Keywords：rolling bearings；vibration；finite element analysis；stress

（责任编辑 贾慧鸣）

The finite element analysis of cylindrical roller bearings

WANG Jun－ling，ZHENG Xiang＊，WU Huan
（Sch of Mech Engin，Yangzhou Univ，Yangzhou 225127，China）

TH 133.3

A

1007－824X（2012）02－0043－04

2011－12－23

国家自然科学基金资助项目（50975249）

＊联系人，E－mail：xzheng9＠163.com