倾斜岸河流和水库水面污染带下的污染物质量浓度分布

武周虎，贾洪玉

(1.青岛理工大学环境与市政工程学院，山东 青岛 266033;

2.山东省建设项目环境审核受理中心，山东 济南 250013)

各种废弃物越来越多地出现在河流和水库水面，如来源复杂、种类繁多的各类垃圾［1］以及石油类和密度较小的污水等。这些水面污染物不仅影响自然景观，而且污染深层水体，会给水环境与水生态带来危害。国内外对水面污染源向水下的一维扩散研究已取得一定成果［2-3］，但倾斜岸河流和水库水面污染源向水下的扩散是立面二维问题，对此问题的研究尚不多见。武周虎等［4-5］采用解析法和数值方法分别给出了水面半无限和有限长油膜下油滴输移扩散方程的解析解和数值解。武周虎［6-7］还采用解析方法给出了水库倾斜岸坡地形岸边点源排放各向同性扩散条件下的污染混合区计算方法和简化条件。在此基础上，武周虎等［8-9］基于镜像法原理和角形域平面镜映射试验，给出了各向异性扩散条件下的角形域映射图，进而给出倾斜岸坡地形岸边点源排放各向异性扩散条件下的污染物质量浓度分布的理论解。韦细姣［10］对龙江金城江区段进行水污染调查，利用二维水质数学模型进行水质达标分析。薛红琴等［11］在考虑了两岸边界的一次反射、污染物的降解和背景值共同影响的条件下，给出排污口在任意位置处的污染带特征参数的计算方法。顾莉等［12］从河道分汊口、交汇口、水流特性及污染物输移特性等4个方面总结了分汊型河道的水流运动特性和污染物输移扩散规律的相关研究成果，提出亟待加强不同排放方式和不同分汊形态下污染物输移机制等问题的研究。武周虎［13］基于各向异性扩散条件下的静止水体中瞬时线源二维扩散的解析解，推导了半无限水面瞬时污染源下和倾斜岸角形域中二维扩散污染物质量浓度分布的理论公式，其局限性在于不能用于常见的岸边水面任意宽度瞬时污染源情况下的扩散计算。

本文针对文献［13］半无限水面瞬时污染源的局限性，基于横向和垂向扩散系数不相等时静止水体中瞬时线源二维扩散的解析解，推导水面有限宽(任意宽度)瞬时污染源二维扩散的溶解性污染物质量浓度分布，并在顺直倾斜岸坡大宽度深水情况下借助于角形域映射图［8-9］，推导出倾斜岸水面瞬时污染带下角形域中二维扩散污染物质量浓度分布的理论计算公式，并分析其合理性及应用范围。

1 水面有限宽瞬时污染源下的二维扩散

如图1所示，在静止水体半无限空间的半无限水面上(y≥0，z=0)，存在等强度水面有限宽瞬时污染源(带)，污染源宽度L＞0，取垂直于yOz平面x方向的单位长度进行分析。

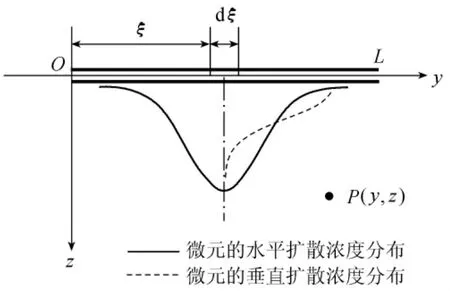
图1 水面有限宽瞬时污染源下的二维扩散

将水面有限宽瞬时污染源看作由无数个微小的污染线源或微元(即yOz坐标系上的点源，下同)dξ所组成，每个微元的质量为dM=mdξ，其中m为水面污染源强度，对每个微元来说它都要向下、向左和向右边扩散。设在水面下有一个点P，其坐标为(y，z)，P点到某个污染微元的水平距离为y－ξ，垂直距离为z，在指定时刻P点的污染物质量浓度C(y，z，t)应等于水面各微小污染源扩散到P点的污染物质量浓度dC的叠加。根据文献［13］，任意一个微小水面污染源扩散至水下P点的污染物质量浓度为

式中:Ey和Ez分别为横向和垂向扩散系数。

式(1)中ξ从零到L上积分，可以得到由水面有限宽瞬时污染源引起P点的污染物质量浓度为

根据误差函数 erf(x)的性质，对于固定的(z，t)值，由式(5)得到C(±∞，z，t)=0，Cmax(y，z，t)=C(L/2，z，t);对于固定的(y，t)值，由式(5)得到Cmax(y，z，t)=C(y，0，t)，C(y，∞，t)=0，沿水深的污染物质量浓度分布为半正态曲线。进一步分析发现随着扩散历时t的增大，污染物的最大质量浓度减小，但扩散影响深度和横向影响范围扩大。

在式(5)中取m=200 g/m2，Ey=0.1 m2/s，Ez=0.01 m2/s，t=1 800 s，L=25 m，计 算 得 到C(0，0，1800)=C(25，0，1800)=10.80 mg/L，Cmax(12.5，0，1800)=13.03 mg/L，并依次计算z=0，z=5 m，z=10m等深线和y=－25 m，y=0，y=25 m 垂线上的C(y，z，1800)。图2分别给出了静止水体中水面有限宽瞬时污染源下相应等深线和垂线上的污染物质量浓度分布曲线。由图2可以看出，静止水体中水面有限宽瞬时污染源沿水深的质量浓度服从半正态曲线分布，同一y值水面上的质量浓度最大，无限深处质量浓度为零。由于水面有限宽瞬时污染源位于L≥y≥0处，y＜0和y＞L区域的质量浓度是由L≥y≥0区域的污染物扩散产生，所以对同一z值的横向质量浓度分布在污染源中间y=L/2点下方出现最大值，中间区域出现较平的一段，向两侧呈对称递减趋势。当水面瞬时污染源宽度L很小时，沿横向的质量浓度分布接近正态曲线。

图2 水面有限宽瞬时污染源下的污染物质量浓度分布

2 倾斜岸水面瞬时污染带下的二维扩散

在顺直倾斜岸坡大宽度深水条件下，水面有限宽瞬时污染带下角形域中的二维扩散见图3(a)，定义域为y≥0，ytanθ≥z≥0。根据文献［8］给出的横向和垂向扩散系数不相等的角形域映射原理，图3(b)给出了倾角θ=60°的角形域映射质量浓度分布叠加示意图。

图3 倾斜岸水面瞬时污染带下的二维扩散

在图3(b)中，C0(y，z，t)为水面实源产生的二维质量浓度分布，C1(y，z，t)和C2(y，z，t)分别为水面等强度像源和二重像源产生的二维质量浓度分布。C0(y，z，t)的表达式为式(5)，C1(y，z，t)和C2(y，z，t)的表达式分别为式(5)中(y，z)坐标旋转2θ和4θ得到，即像源和二重像源产生的二维质量浓度分别为

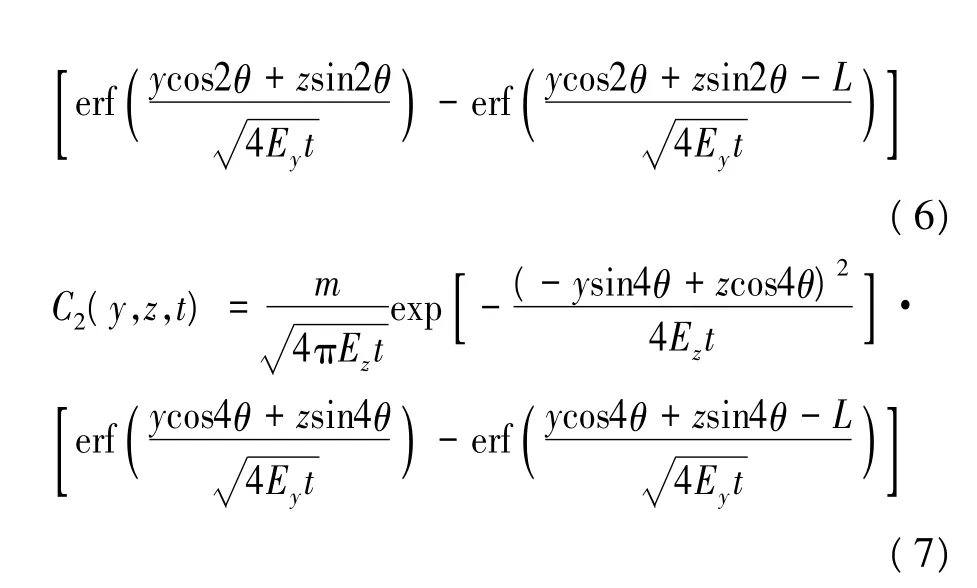
按照扩散方程单独解的叠加原理，水面有限宽瞬时污染源下角形域中的二维质量浓度分布等于实源、像源和二重像源在定义域内对应坐标点产生的质量浓度分布的叠加，即C(y，z，t)=C0(y，z，t)+C1(y，z，t)+C2(y，z，t)。那么，倾斜岸水面瞬时污染带下θ=60°角形域中的二维质量浓度分布为

根据文献［8］的归纳结果，当倾角参数n(n=180°/θ)为自然数时，由式(8)得到倾斜岸水面瞬时污染带下角形域中的二维质量浓度分布为

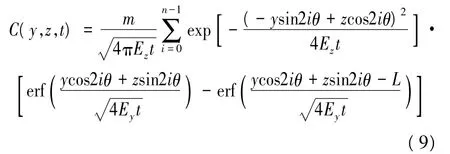
3 分析与讨论

在式(9)中取L=25m，m=200g/m2，Ey=0.1m2/s，Ez=0.01 m2/s，t=1800s，C(0，0，1800)=10.8nmg/L。分别计算岸坡倾角为 θ=30°，36°，45°，60°和90°(即n=6，5，4，3和2)时，各倾角水面、沿z=ytanθ的倾斜岸坡和y=12.5 m垂线上的污染物质量浓度分布以及各角形域中C=10 mg/L的等质量浓度线分布，见图4～7。

图4 各倾角水面污染物质量浓度分布

图5 沿倾斜岸坡的污染物质量浓度分布

图6 y=12.5 m垂线上的污染物质量浓度分布

图7 各角形域中C=10 mg/L的等质量浓度分布线

由图4和图5可以看出，受倾斜岸坡角形域边界反射产生质量浓度叠加的影响，倾角越小，倾斜岸坡顶点质量浓度越高，倾斜岸坡顶点质量浓度与倾角大小成反比，且计算点距离岸坡顶点越近，质量浓度越大;反之，质量浓度越小，当横坐标y(图4)或沿倾斜岸坡向水下延伸的距离(图5)趋于无穷大时质量浓度趋于零。各倾角下水面横向质量浓度分布和沿倾斜岸坡的质量浓度分布均为单调下降曲线，并以零质量浓度线为渐近线;当 θ=36°(n=5，n为奇数)与 θ=60°(n=3，n为奇数)时，水面横向质量浓度分布随横坐标y的增大先下降到θ=90°时水面横向质量浓度线之下，而后在其下方以该质量浓度线为渐近线。θ=36°(n=5，n为奇数)与 θ=45°(n=4，n为偶数)时水面横向质量浓度分布线出现交叉现象，θ=60°(n=3，n为奇数)与 θ=45°(n=4，n为偶数)时沿倾斜岸坡的质量浓度分布线出现交叉现象，反映了n为奇、偶数时角形域的边界反射产生质量浓度叠加的影响规律不同。

由图6可以看出，各角形域在y=12.5 m垂线上的质量浓度分布随水深的增大单调减小，θ=60°，90°和45°时y=12.5m垂线上的质量浓度分布出现交叉现象。由图7可以看出，各角形域中C=10 mg/L的等质量浓度分布线沿倾斜岸坡出现向下扩散的趋势，在远离倾斜岸坡时等质量浓度分布线向水面上升并出现双重变化特征:一是当θ=36°(n=5，n为奇数)与 θ=60°(n=3，n为奇数)时，C=10 mg/L 的等质量浓度分布线随横坐标y的增大与θ=90°等质量浓度分布线交叉;二是当θ=30°(n=6，n为偶数)与 θ=45°(n=4，n为偶数)时，C=10 mg/L 的等质量浓度分布线随横坐标y的增大呈单调上升趋势，并以θ=90°等质量浓度分布线为渐近线。这主要取决于在不同倾角时实源、像源和二重像源的分布位置和二维质量浓度分布的叠加。

由以上分析结果可以看出，倾斜岸水面瞬时污染带下二维扩散污染物质量浓度分布具有随n为奇、偶数而不同的特性，讨论如下:

a.当 θ=180°(n=1)时，具有水面一次边界反射的污染物扩散为角形域扩散的特例，由式(9)得到水面有限宽瞬时污染源条件下二维扩散的污染物质量浓度分布为

定义域为y≥0，∞＞z＞－∞。这一结果与式(5)完全一致。

b. 当 θ=90°(n=2)，且水面污染源宽度L→∞时，具有水面和垂直岸各一次边界反射的污染物扩散为角形域扩散的另一个特例，由式(9)得到半无限水面瞬时污染源条件下二维扩散的污染物质量浓度分布为

定义域为y≥0，z≥0。式(11)表明污染物质量浓度分布与横坐标y和横向扩散系数Ey无关，这一结果与文献［2］水面有边界反射的瞬时平面源一维(垂向)扩散的结果完全一致。

c.当角形域内为各向同性扩散(Ey=Ez=E)水体时，对于沿z=ytanθ倾斜岸坡的等强度有限宽瞬时污染源，角形域中二维扩散污染物质量浓度分布的理论计算公式可由式(9)进行坐标旋转得到:

取Ey=Ez=E=0.01 m2/s，L=25 m，其他参数同前，分别采用式(9)和式(12)计算 θ=45°，60°和 90°时水面和岸坡有限宽瞬时污染源条件下的污染物质量浓度分布，进行C=10 mg/L的等质量浓度线分析比较，见图8。由图8可以看出，水面与倾斜岸坡有限宽瞬时污染源在角形域中形成的等质量浓度线为相应倾角角平分线的对称曲线，即对于角形域内的各向同性扩散，水面有限宽污染源向水下的扩散与倾斜岸水面有限宽污染源向上的扩散和边界反射的机理相同，因此其等质量浓度线是以角平分线为对称轴的对称曲线。

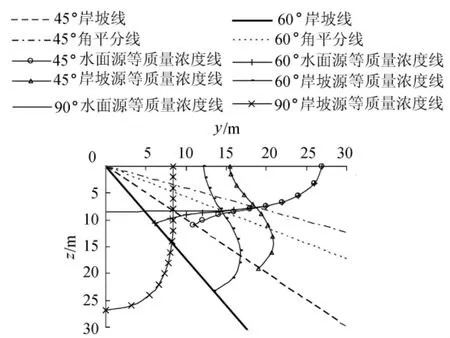
图8 水面与岸坡有限宽瞬时污染源条件下C=10 mg/L的等质量浓度线比较

d.当水面污染带宽度L→∞时，式(9)变为

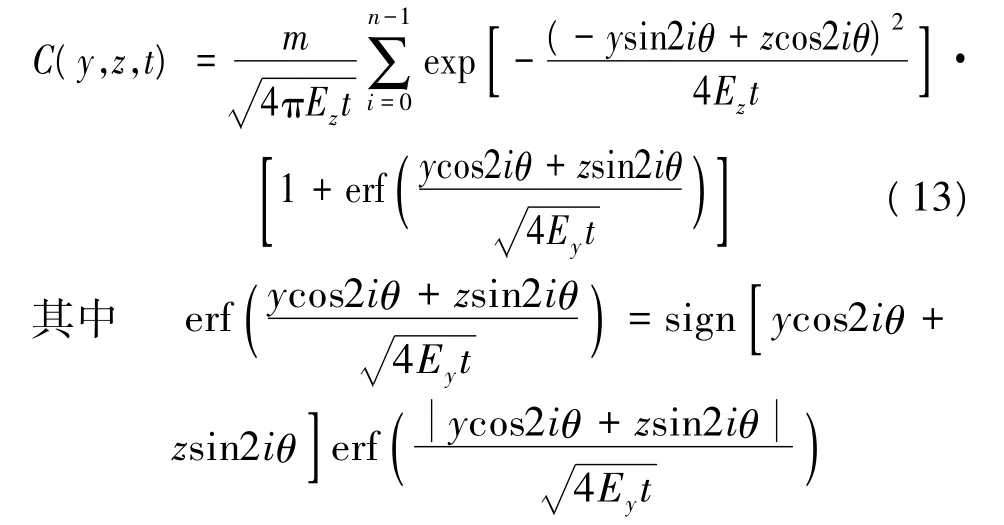
当自变量小于零时，利用误差函数是奇函数的性质进行计算。这一结果与文献［13］半无限水面瞬时污染源在角形域中相应条件下扩散的质量浓度分布完全一致。

以上讨论说明了文中倾斜岸水面瞬时污染带下二维扩散的污染物质量浓度分布理论计算公式的合理性。

4 结论

a.在横向和垂向扩散系数不相等的条件下，经过严格的数学推导，给出了水面有限宽瞬时污染源和倾斜岸水面瞬时污染带条件下二维扩散污染物质量浓度分布的理论计算公式。

b.在倾斜岸水面瞬时污染带条件下，角形域倾角对污染物的质量浓度分布影响较大，角形域内质量浓度分布具有随倾角参数n为奇、偶数而不同的特性。

c.计算点距离岸坡顶点越近，角形域倾角对污染物质量浓度分布的影响越大;横坐标越大，影响越小;水深越大，影响也越小。

d.本文所推导的公式适用于顺直倾斜岸坡大宽度深水情况，满足倾角参数n为自然数的倾斜岸水面瞬时污染带条件下二维扩散污染物质量浓度分布的计算。

:

［1］陈海滨，张黎.水面垃圾污染控制初步研究［EB/OL］.［2012-02-02］.http://www.cn-hw.net/html/32/200804/6380.html.

［2］FISCHER H B，IMBERGER J，LIST E J，et al.Mixing in inland and coastal waters［M］.New York:Academic Press，1979.

［3］余常昭，马尔柯夫斯基M，李玉梁.水环境中污染物扩散输移原理与水质模型［M］.北京:中国环境科学出版社，1989:152-160.

［4］武周虎.水面油膜下油滴输移扩散方程的解析解［J］.海洋环境科学，2000，19(3):44-47.

［5］武周虎，尹海龙.水面有限长油膜下油滴浓度分布及其污染带的数值计算［J］.水动力学研究与进展:A辑，2001，16(4):481-486.

［6］武周虎.倾斜岸水库污染混合区的理论分析及简化条件［J］.水动力学研究与进展:A 辑，2009，24(3):296-304.

［7］武周虎.水库倾斜岸坡地形污染混合区的三维解析计算方法［J］.科技导报，2008，26(18):30-34.

［8］武周虎.倾斜岸坡角形域顶点排污浓度分布的理论分析［J］.水利学报，2010，41(8):997-1002，1008.

［9］武周虎，徐美娥，武桂芝.倾斜岸坡角形域顶点排污浓度分布规律探讨［J］.水力发电学报，2012，31(6):166-172.

［10］韦细姣.龙江金城江区段污染物质量浓度的分析［J］.水资源保护，2004，20(6):56-68.

［11］薛红琴，刘晓东.连续点源河流污染带几何特征参数研究［J］.水资源保护，2005，21(5):23-26.

［12］顾莉，华祖林，褚克坚，等.分汊型河道水流运动特性和污染物输移规律研究进展［J］.水利水电科技进展，2011，31(5):88-94.

［13］武周虎.倾斜岸河库水面污染源下浓度分布的理论分析［J］.水动力学研究与进展:A 辑，2012，27(4):449-455.