基于粒子群算法的宝鸡市水资源优化配置研究

秦 涛

(陕西省引汉济渭工程协调领导小组办公室，陕西 西安 710032)

基于粒子群算法的宝鸡市水资源优化配置研究

秦 涛

(陕西省引汉济渭工程协调领导小组办公室，陕西 西安 710032)

水资源配置的目标是满足人口、资源、环境以及经济与水资源在时间、空间、数量以及质量上的协调发展，使有限的水资源获得最大的利用价值，推动区域社会经济进步，实现可持续发展。以经济效益、环境效益、社会效益等综合效益作为最佳优化配置目标，建立宝鸡市水资源优化配置模型。利用粒子群算法搜索速度快、效率高，算法简单的特点，用粒子群算法求解模型结果，最后通过经济、技术和生态环境分析论证与比选，确定优化配置方案。

宝鸡市;水资源;优化配置;粒子群算法

水资源是人类生存发展的物质基础，是可持续发展的重要保障。随着人口的不断增长、社会经济的快速发展、生态环境的不断恶化，水资源短缺问题已成为制约一个地区、国家乃至全球发展的重要因素［1－3］。水资源优化配置是研究如何合理开发利用水资源，提高水资源的配置和利用效率，实现水资源的可持续利用，保证社会经济、资源、生态环境的协调发展［4－6］。

1 水资源优化配置模型的建立

1.1 目标函数的确定

本次配置以可持续发展理论为基础，强调社会经济—人口—资源—生态环境的协调发展，遵循水资源的供需平衡、时间和空间上的水量和水质统一控制［7－8］。因此，对于宝鸡市水资源优化配置是多目标的，以经济效益、环境效益、社会效益等综合效益最佳为优化配置目标。

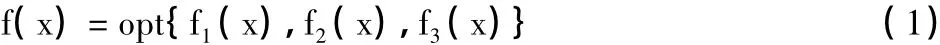
目标1(经济效益):各水平年各子区不同行业供水产生的经济净效益最大。

目标2(社会效益):各水平年各子区供水系统总缺水量最小。

目标3(环境效益):各水平年各子区COD排放量之和最小。

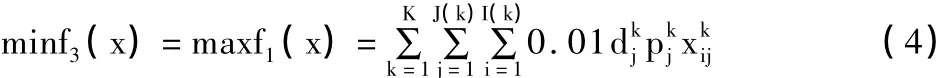
1.2 水资源优化配置的约束条件

多水源供水优化配置的目的是确定最合理的各水源供水量，一方面，希望供水量尽量达到配置目标，反映在优化模型的目标函数值最大或最小;另一方面，各种水源进行供水时，受配置原则、各水源自身的供水能力和相应的供水配套设施的限制，各水源的供水量必须符合一定的条件，反映在优化模型的约束条件集合上。

1.2.1 水源可供水量约束

1.2.2 水源输水能力约束

1.2.3 用户需水能力限制

1.2.4 非负约束

1.3 水资源优化配置模型的参数确定

1.3.1 效益系数的确定

1)工业用水的效益系数工业总产值分摊方法确定，计算公式如下:

式中:b指工业用水效益系数;β指工业用水效益分摊系数，不同的取水水源，其分摊系数不同:以自来水作为取水水源，工业供水效益分摊系数取5%;以自备井作为取水水源，工业供水效益分摊系数取4%;以水利工程作为取水水源，工业供水效益分摊系数取8%;指工业万元产值取水量(m3/万元)。

2)农业用水效益系数按灌溉后的农业增产效益乘以水利分摊系数确定。

3)生活、环境及公共设施用水的效益是间接而复杂的，不仅有经济方面的因素，而且有社会效益存在，因而其效益系数比较难确定。根据生活、环境用水优先满足的配置原则，本文在计算中赋以较大的权值，用以表示其效益系数。

根据以上方法进行，以现状年计算确定，宝鸡市工业用水效益系数为10.07元/m3，农业用水效益系数保证率75%下为5.49元/m3，生活、生态环境用水效益系数为10.94元/m3。

1.3.2 费用系数的确定

1)从水厂取水的用户以水价作为其费用系数。

2)从自备井取水的用户以水资源费、污水处理费与提水成本之和作为其费用系数。

3)从水利工程取水的用户以水资源费、污水处理费与输水成本之和作为其费用系数。

4)农业用户的费用系数参考水费征收标准确定。

根据宝鸡市现状年水费征收标准，本次计算中工业用水费用为2.25元/m3、农业用水费用为 0.23元/m3、居民生活、生态环境用水费用为2.24元/m3。

1.2.3 目标权重的确定

确定权重的方法很多，主要分为主观赋权法、客观赋权法和组合赋权法三类。本文运用二元对比法来确定目标权重系数。具体方法如下:

1)对于个目标，慎重考虑其重要度，按重要程度由高到低进行排序。

2)使用以下六种模糊语气表示第一个目标(最重要目标)与其他目标相比较时的相对重要程度:同样重要、略为重要、明显重要、十分重要、极其重要、无可比拟。

表示第一个目标与第个目标相比较时的重要度，由于第一个目标与其本身比较因为“同样重要”，故=0.5，第一位的目标最多是“无可比拟”地重要于最后的第个目标，即，其他语气重要度可按0.5至1.0间的线性变化内插求得。可见，应满足:

3)将u1j(j=1，2，…，m)带入下式，求得各目标的重要度:

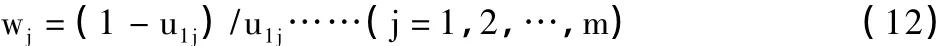
根据宝鸡市的具体情况，根据上式确定出渭滨区、金台区、陈仓区、凤翔县、岐山县、扶风县、眉县、陇县、千阳县、陇县、麟游县、凤县、太白县的子区权重系数依次为 w1=0.1，w2=0.1，w3=0.1，w4=0.08，w5=0.08，w6=0.08，w7=0.08，w8=0.076，w9=0.076，w10=0.076，w11=0.076，w12=0.076。经济、社会和环境目标权重系数分别为 λ1=0.45，λ1=0.3，λ1=0.25。

1.3.4 用户需水量的上下限的确定

(1)生活需水量的上下限

考虑生活用水的特性，生活需水量的上下限均为其需水量，即:==式中:，分别为生活需水量的上下限，规划水平年 k子区生活用水需水量。

(2)一般工业、建筑业和服务业需水量的上下限

考虑工业用水的特征，工业需水量的上下限按下式取

(3)环境需水量的上下限

考虑到人们对环境用水的重视，环境用水的上下限也均取为环境需水量，即

(4)农业灌溉需水量的上下限

农业灌溉需水量的上下限需要根据有效灌溉面积、保证灌溉面积和综合灌溉定额来确定，即

1.3.6 污水排放系数、水质目标

宝鸡市污水排放的主要用户为城镇生活和工业，其中最普遍、最严重的污染因为是 COD(化学需氧量)，因此只有COD总排放量最小，环境效益才能达到最优，根据多年的实测资料，宝鸡市城镇生活和工业排放的污水中污染物的平均浓度分别为 258.6 mg/L、167.3 mg/L，污水处理后的浓度为20 mg/L，满足国家地表水环境质量标准(GB3838－2002)。城镇生活和工业污水排放系数0.71、0.58。

2 粒子群算法

2.1 粒子群算法原理

PSO算法数学表示如下:假设在一个维的目标搜索空间中，有m个粒子组成一个群落，其中第 i个粒子表示为一个N维的向量，(i=1，2，…，m)即粒子 i在 N维的搜索空间中的位置是xi。换言之，每个粒子的位置就是一个潜在的解。将代入一个目标函数就可以计算出其适应值，根据适应度值的大小衡量的优劣。粒子 i的“飞行”速度也是一个N维向量，记为=(vi1，vi2，…，viN)，(i=1，2，…，m)。记粒子 i迄今为止搜索到的最优位置为，整个粒子群迄今为止搜索到的最优位置为=(pg1，pg2，…，pgN)。Eberhart和Knnedy最早提出的 PSO算法利用下列公式对粒子做更新操作:

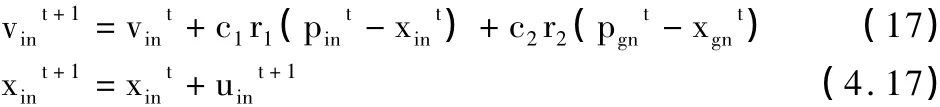
式中:i=1，2，…，N;c1和 c2为学习因子，变化范围为［0，4］，一般取 c1=c2=2;r1和 r2是在［0，1］之间的产生的随机数;vin∈［－ vmax，vmax］，vmax是常数，一般来说，vmax多设置为粒子在该维最大变化范围的10%～40%。

结合水资源优化配置问题及PSO算法的特点，可以通过对PSO算法中粒子编码、适应度函数的构造、约束条件的处理等几方面的调整实现这一优化问题的求解。

2.2 粒子的编码

根据建立的优化配置模型的特点，设定粒子是第 i水源向第k子区第 j部门的供水量xijk，一个粒子采用二维数组进行编码，即:

式中:n为用水部门个数;SL为子区个数;si为第 i个子区水源个数;s为所有子区内的水源个数，即:

采用这种形式的粒子编码，直接反映了各水源在各部门之间的配置情况，将某一行的数值相加即可得到该水源的实际利用情况，将一个子区范围内的某一列数值相加即可得到该子区这一列对应部门的实际配水量。

2.3 适用度函数的构造

适应度函数要能反映水资源优化配置模型中所有目标的综合效果。由于用来衡量各目标的指标量纲不同，且优化准则也不一致，有的是越大越好，如国内生产总值、粮食产量、供水保证程度等;有的是越小越好，如环境损失、供水费用等。因此，直接用目标函数表达式作为适应度函数的方法已不能奏效，要寻求构造适应度函数的新的方法。

将目标j可以达到的最好水平Yjbest对应的标准值设定为1，最差水平 Yjworst对应的标准值设定为0.01，用下面的插值公式计算该目标对应的标准值，即:

对经济目标:

对社会目标和环境目标:

将各个目标转化为0～1之间的标准值后，就可以将这些标准值通过加权和的方法构造出适应度函数，即

式中:particle为计算的粒子;ob为目标的个数。

2.4 约束条件的处理

采用约束性适应度函数法、罚函数法等方法来处理约束条件，对约束较少的优化问题是有效的，但难以解决水量优化配置模型这样的约束条件多、相互制约关系复杂的问题。原因在于约束适应度函数和罚函数将变得非常复杂，且各约束的权重都将变得非常小和难以确定。

结合水量优化配置模型的特点，提出模型约束条件处理的可行解修正函数法，保证了每一次迭代的粒子都是最优解，且提高了迭代过程的收敛速度。

水量统一优化配置模型的约束条件可归为两大类:即“≥”型和“≤”型。针对两种类型的约束，分别采用下列方法对粒子进行相应的修正。

1)“≥”型约束的修正方法:这一类型的约束，如水源可利用量的约束。在粒子迭代过程中，当不能满足约束条件，对与这一约束相关的粒子单元作如下修正，即

2)“≤”型约束的修正方法:模型中的这类约束条件，主要指用水部门需水下限。对不满足这类约束的粒子单元的修正过程需要考虑的内容较多，修正的方法也相应复杂许多。这是因为在对粒子值的增大过程中要受到已经修正过的水源可利用量及其相关部门供水能力的双重限制，而且还要尽可能保证粒子位置出现的随机性不受破坏。

针对需水下限约束，当向某一部门的配水量达不到其下限要求时，要作两个判断:一是存在供需关系的水源向该部门的供水能力是否已达到供水上限;二是这些水源的可利用量是否已经达到极限。

如果两者都是否定，则说明这些水源具有向该部门进一步增加供水的能力。将所有这些相关水源的“可增加”供水能力统计后，就可以根据缺水情况，按照这一供水能力比例，对相关粒子单元进行修正。即

综上所述，用修正函数处理约束条件的过程为:首先是对水源的可利用量约束进行修正，其次是超过需水上限约束的修正，最后是针对生活和生态环境用水优先的水量调整。

2.5 PSO算法用于水资源配置模型的求解流程

针对本文提出的水资源配置模型，经过对粒子进行编码、构造目标适应度函数、处理约束条件，采用式4.17所示的粒子更新方程，即可实现对水量统一优化配置模型的求解。综上所述，采用PSO算法求解宝鸡市水资源优化配置问题的步骤归纳如下:

Step1:在解空间内(由供输水能力约束与非负约束条件构成)随机产生初始粒子。

Step2:判断粒子是否满足约束条件，如不满足，则调用修正函数，对粒子进行调整，使之成为可行解。

Step3:根据公式(22)计算每个粒子的适应值。

Step4:比较每个粒子的适应值与个体极值，从中选取全局最优粒子。

Step5:根据式(17)、(18)更新每个粒子的位置和飞行速度。在迭代过程中，如果计算出的速度超过了最大速度限制，则将其值设定为最大速度;如果粒子某一维的位置超过了初始粒子的生成空间，则设定粒子在这一维的位置为此维生成空间的对应极值。

Step6:如果达到预先设定的停止准则(通常为最大迭代次数)，则输出计算结果，否则转到Step3。

3 宝鸡市水资源优化配置及分析

根据上述水资源优化配置模型，利用PSO算法进行模型求解。宝鸡市供水水源分为3类，分别为地下水，地表水，其他水源;用水部门分为6类，分别为生活用水、一般工业用水、建筑业、服务业、农业用水及生态环境用水。选择来水保证率为75%的规划水平年2020年与2030年进行水资源的优化配置，得到了水资源配置结果，并通过水资源供需平衡，对水资源配置结果进行分析。

根据2020、2030两个规划水平年的水资源配置结果可知，水源的供水情况基本上满足中国目前城市“优先开发当地水源，积极利用再生水源，充分引用外调水”和“严格控制地下水”的用水原则。在2020规划水平年中，由于加大当地水源工程的建设，增大污水回用率，并在引汉济渭工程建成后，石头河水库不再向西安市和咸阳市供水，石头河水库的供水完全用于宝鸡市的国民经济发展中，这大大提高了宝鸡市的供水量。2030年规划水平年中，由于宝鸡市水资源开发利用潜力已经达到基本饱和，主要考虑外流域调水以满足宝鸡市国民经济快速健康的发展，引汉济渭工程成为宝鸡市的主要供水水源，总的来说，这样一些地区由于地下水超采引起的缺水问题可以基本得到解决。全市缺水状态总体上得到了有效的缓解。

在遵循“优先保证生活和生态用水”的原则下，生活及生态部门用水量得到了完全满足，缺水量一般只能在工业和农业两个用水部门中出现。水资源优化配置结果表明，2020年宝鸡市农业和工业的缺水率分别为2.4%和2.1%;2030年宝鸡市农业和工业的缺水率都小于3%。结果从一个方面说明了配置模型中约束条件设置、修正机制的有效性、可行性。同时，工业和农业的需水满足情况在也均有不同程度的提高，这也说明对优化配置多目标模型的求解方法是可行的。

从宝鸡市水量利用情况看，存在着水资源可利用量有富裕下供水却不能满足需水要求的情况。主要原因是受地理位置、地形条件造成的水资源量分布不均导致部分子区缺水;另一方面也与工程设施和供水布局造成的部分部门供水能力不足等条件制约有关。

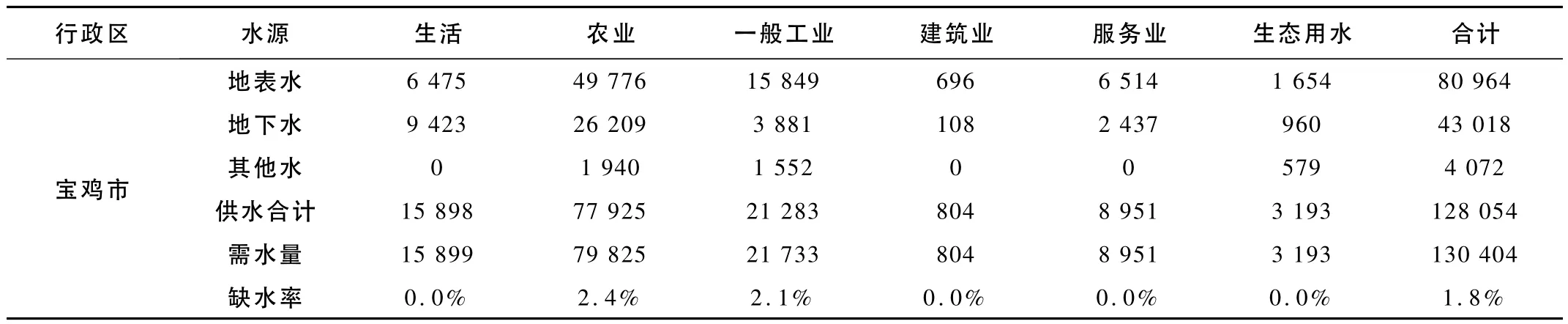
表1 2020年P=75%宝鸡市水资源优化配置结果 万m3

表2 2030年P=75%宝鸡市水资源优化配置结果 万m3

［1］吴泽宁，索丽生.水资源优化配置研究进展［J］.灌溉排水学报.2004，23(2):1—5.

［2］谢新民，赵文骏，裴源生等.宁夏水资源优化配置与可持续利用战略研究.中文1版郑州:黄河水利出版社.2002.

［3］王劲峰，刘昌明等.区际调水时空优化配置理论模型探讨.水利学报.2001，4:7—1［21］.

［4］张勇传等.微分动态规划及回归分析在水库优化调度中的应用［J］.水电能源科学.1987.19.

［5］赵建世，王忠静，翁文斌.水资源复杂适应配置系统的理论与模型.地理学报.20026:629—647.

［6］张玉新，冯尚友.多目标动态规划逐次迭代算法［J］.武汉水利电力学院学报.1988.

［7］贺北方，周丽等.基于遗传算法的区域水资源优化配置模型.水电能源科学.2002.3:10—13.

［8］王立正.人民胜利渠灌区水资源优化配置模式探讨.人民黄河.2004，26(9):26—28.

Research on Water Resources Optimal Allocation Based On Particle Swarm Calculation in Baoji City

QIN Tao
(Diversion Project Coordination Leading Group Office from Hanjiang to Wei River in Shaanxi Province，Xi’an 710032，Shaanxi)

The objective of water resources allocation is to meet requirement of coordinated development between population，resources，environment，economic and the time，space，quantity，quality of water resources，which produce concrete results on maximizing the use value of limited water resources，promoting the regional economic and social progress，and realizing the sustainable development.The model of water resources allocation of Baoji is set up，in order to achieve a best optimized comprehensive benefits allocation of economic，environmental，social and others.The result of this model is fully explained by the solution of Particle Swarm Optimization.The method of PSO enjoys many obvious advantages such as high search speed，great efficiency，easy accessibility，to name just a few.The paper gives a finally optimization allocation scheme upon analytic demonstration and comparison of economy，technology and environment.

Baoji City，water resources，optimal allocation and particle swarm optimization

TV211.1

A

1004－1184(2012)05－0116－04

2012－04－10

国家自然科学基金(项目编号:51079120);国家自然科学基金(项目编号:51109175)

秦涛(1984－)，男，陕西韩城人，硕士研究生，研究方向:区域经济与水资源管理。