“强迫冲突”方法在高等数学教学中的应用*

周志海 王有文

(太原理工大学阳泉学院基础部，山西 阳泉 045044)

“强迫冲突”是一个心理学名词，指用两个截然相反的词来描述同一个对象［1］，例如“黑色的白雪”，体现了一种创造性思维.将这种思维用于高等数学中，可以促成其教学.下面就“强迫冲突”方法的应用，结合极大极小法、导数积分法、有限无限法、无穷大无穷小法、常量变量法分别加以阐述.

1 极大极小法

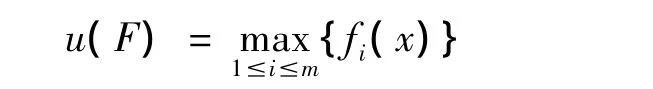
为评价函数，其中F(x)=(f1(x)，…，fm(x))T.

通过上述评价函数u(F)把求解向量数学规划问题转化为求解单目标最优化问题:

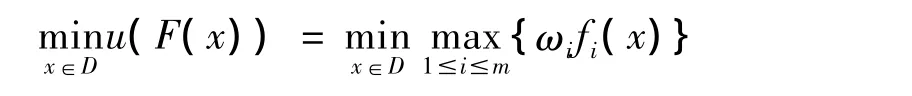
2 导数积分法

分析:直接计算比较困难，可引入一个新的自变量t，将关于x的函数变为二元函数f(x，t)，再进一步求解，求解时将两种逆运算求导数和求积分放在一起.

所以，I(t)满足积分号下的求导法则，故:

3 有限无限法

则:

4 无穷大无穷小法

求极限时将本已矛盾的无穷大和无穷小放在一起，将无穷大转化为无穷小问题，为用洛必达法则铺平了道路.

解 这是未定式∞ －∞，因为

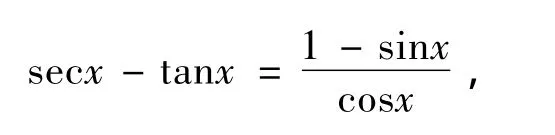
5 常量变量法

处理变量问题时，将一些常量看作变量，将常量和变量相结合，可得到耳目一新的解法.

例5范德蒙行列式的另外一种证法(以四阶范德蒙行列式为例)［3］.

分析:若将范德蒙行列式所有变量中的一个作为变量，其它变量作为常量，可得到另一种证明方法.

2，3，4)，若把D4看作x4的多项式，以x4=x1代入，第1、第4列的元素相等，其值等于零，由余式定理知，D4可被(x4－ x1)除尽.类似地，分别以x4=x2、x4=x3代入知，D4可被(x4－ x2)、(x4－ x3)除尽.同理可证，D4也可被(x3－ x2)、(x3－x1)、(x2－x1)除尽.故D4有因式(x4－x1)、(x4－x2)、(x4－x3)、(x3－x2)、(x3－x1)、(x2－x1).这些因式的乘积展开后对x1、x2、x3、x4来说是6次式，D4展开后也是6次式，故二者之比为常数，即D4=a(x4－x1)(x4－x2)(x4－x3)(x3－x2)(x3－x1)(x2－x1)其中 a 为待定常数.因为D4中有一项的展开式也有一项，二者系数相同，故a=1，得－xj).

此例中首先将x4看作变量，x1、x2、x3看作常量;其次将x3看作变量，x1、x2看作常量;最后将x2看作变量，x1看作常量，使问题得到证明.

［1］李伯黍，燕国材.教育心理学［M］.上海:华东师范大学出版社，1995:351.

［2］解可新，韩立兴，林友联.最优化方法［M］.天津:天津大学出版社，2003:241.

［3］李启文，谢季坚.线性代数的内容、方法与技巧［M］.武汉:华中科技大学出版社，2003:41－42.