三传感器约束多尺度相关管道漏点定位方法

张建利，郭卫星

(哈尔滨工业大学市政环境工程学院，150090哈尔滨)

城市供水管道发生泄露时，在漏口处形成声源，以弹性波的形式沿管道向两方向传播.传统的两传感器相关法，就是利用这两方向的声波信号传到对应传感器间的时延进行漏点定位的，但传统相关法存在如下问题:1)在传统相关法检漏中声波在管道中的传播速度是根据管材和管径作为已知量选取的［1］，实际使用中的管道参数不可避免地存在差异［2］，且由于管道在不同埋设条件下具有不同的速度频散特性［3］，所以速度作为固定量输入必然会存在误差.2)在传统相关法的信号模型中假设源信号和两个传感器中携带的噪声信号是两两互不相关的零均值平稳随机信号［4］，但实际情况是现场存在各种各样的噪声，当噪声间相关时，就可能出现错误的时延估计，产生误检.当噪声较强时，可能将有用信号覆盖，检测不到源信号，结果产生漏检［5］.3)广义相关法虽然已经考虑了噪声的影响，通过权函数ψ(f)的设计提高了信号的信噪比［6］，但是不同的滤波加权函数适用于不同的信噪特征，所以权函数的选择依赖于对信号和噪声的统计先验信息，而实际现场环境下噪声信号的特性难以预测，而且当噪声功率较大时，估计结果的误差也必然较大.4)传统的滤波方法都有1个基本假设，即假定信号和噪声处于不同的频带，滤波除噪即是根据一定的噪声统计特征，将噪声所在的频率范围内的分量一并置零［7］.实际上管道泄露信号分布的频带会根据材质，管径，传播距离等条件的不同有所改变，而噪声的频带难以预测，在整个频率轴上的分布都有可能，所以已有研究曾提到，若直接将采集信号经过高频带通滤波预处理后，并不能得到好的定位结果，甚至远距离检测时，这样处理后会检测不到漏点的存在［8］.

1 三传感器约束多尺度相关漏点定位原理

1.1 基于三传感器的漏点定位模型

本文提出的一种基于3个传感器约束的多尺度相关管道漏点定位方法，不仅能实现比传统两传感器法更准确的定位，而且还解决了传统两传感器法的速度输入不准确的问题，模型如图1所示，图中1、2、3为3个相同的加速度传感器.

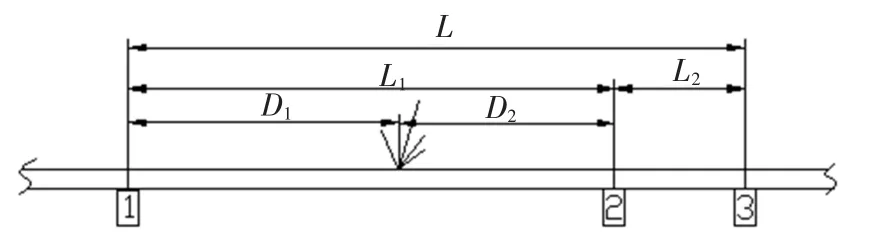
图1 基于三传感器的漏点定位模型示意图

图1中3个传感器任意两个之间的距离是可知的，即L、L1、L2是可知的，同样对应的任意两个传感器之间的时延(即 τ12max、τ23max、τ31max)也是可以求取的.利用其中任意一段距离及其对应的传感器时延就可以实现传统两传感器法定位的功能，本文选用L2和τ23max来计算声波在此管道中的传播速度，选用L1和τ12max进行漏点定位，即

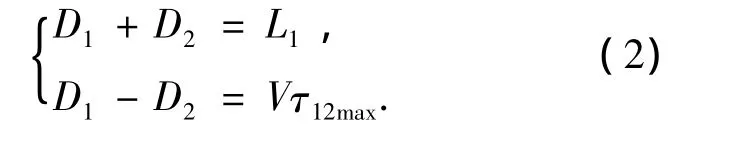
1.2 漏点定位方法及步骤

由三传感器模型可知，时延计算的精度是决定漏点定位准确性的唯一关键因素.为此，本方法通过4个主要步骤来确保时延的计算精度及漏点定位结果的准确性，具体计算流程如图2所示，分别为:多尺度分解(对应图2中的步骤1);多个尺度内求相关时延(对应图2中的步骤2);三传感器矢量匹配筛选(对应图2中的步骤3、4、5);结果显示及判断(对应图2中的步骤6、7).这是本方法区别于两传感器方法的创新.

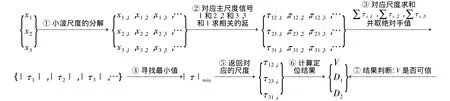
图2 三传感器约束多尺度相关漏点定位计算流程图

1.3 定位原理

1.3.1 多尺度内求相关时延

经同一小波变换后同一尺度内两通道信号的时延保持不变［9］，也就是说小波变换不会造成两通道信号固有时延的失真，这是运用小波进行多尺度分解后计算时延的前提.

将距离漏点不同距离的3个传感器采集上来的3段等长度信号1、2、3统一作8层分解，得到8个尺度内的分信号，然后对每个尺度内近似频带和细节频带下的传感器1、2信号之间，传感器2、3信号之间，传感器3、1信号之间分别做相关计算求取时延 τ12max、τ23max和 τ31max，时延估计结果如图3(a)所示.图3(a)中给出了分辨率从高到低8个尺度内的近似和细节频带下共16组时延估计结果.即每一个频带下时延τ12max、τ23max和τ31max都有1组估计结果.由于多尺度分解良好的信噪分离作用［10］，所以总会有些频带内的源信号的成分比较占优势，而时延估计的精度在很大程度上决定于做相关的两个信号的“纯度”，所以在这些频带上求相关所得到的时延结果也必然比其他频带更接近实际，图3(b)为其匹配结果.1.3.2 三传感器矢量匹配筛选

虽然经过图2中的步骤2得到了多组时延估计结果，见图3(a)，但由于采集信号时各种非源噪声的掺入，从而使结果并非每组都正确，因此有必要找到一种筛选规则，从多组数据中挑选到最优的估计结果.

对应任意2 个通道i，j(i，j=1，2，3，…)之间的时间延迟为

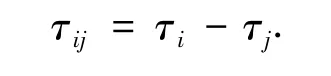
且有

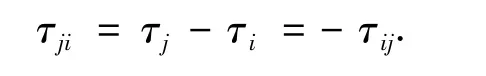
现增加第3通道k，则有

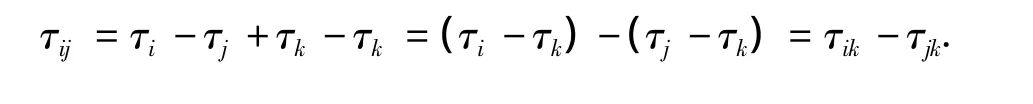
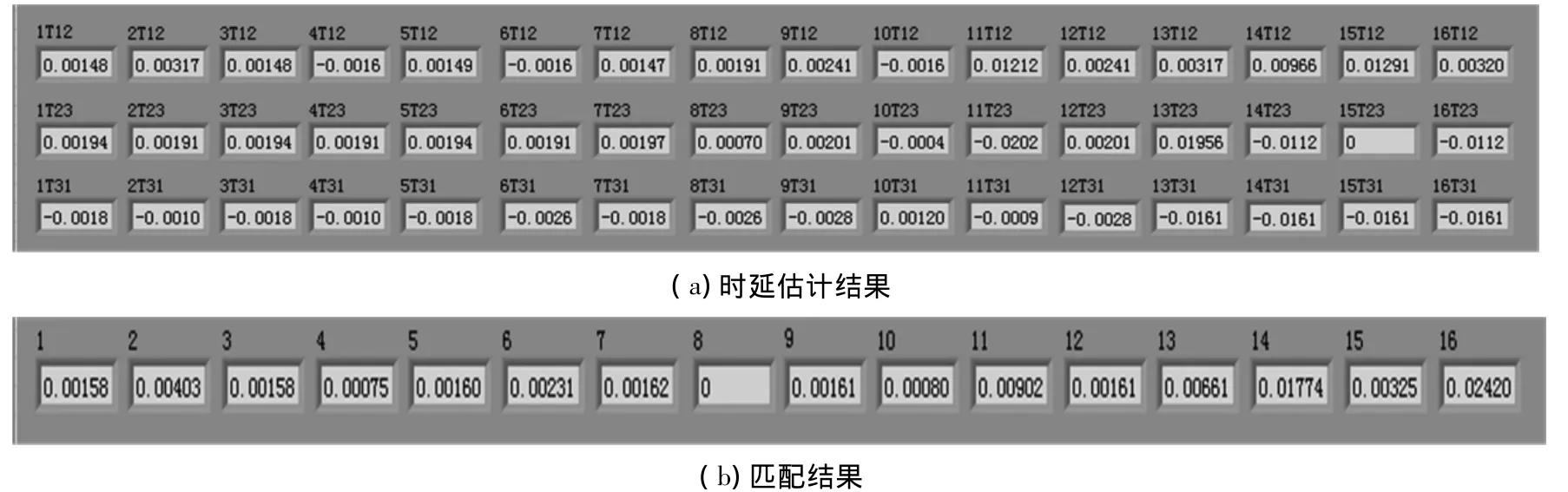
图3 多尺度相关时延估计结果

整理为

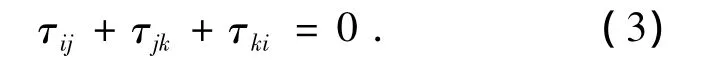
由于式(3)类似于矢量三角形求和，故称为三传感器矢量匹配关系.由于上述关系的推导没有附加其他条件，所以只要3个传感器捕捉到同一个信号源，则它们的时延就必然满足式(3)，对于正常传播的单漏点泄漏源信号同样满足该关系，而各种杂乱的噪声却很少满足该关系.由于图3(a)中每一频带内的时延求取次序正好符合式(3)中的次序，故可以将图3(a)中同一频带内(即每一列)的时延求和来判断对式(3)的匹配程度，匹配结果如图3(b)所示.可见频带8对式(3)匹配得最好，同时此频带内的时延值也是真实情况的反应，其余各频带由于受到噪声不同程度的“污染”而存在相应的误差.因此可将式(3)作为约束法则，根据不同频带内时延求和结果的符合程度(即匹配误差)来筛选最优结果.

1.3.3 计算及结果判断

有了筛选出的最优时延结果，即可利用式(1)、(2)进行漏点定位计算，计算结果如图4所示.

图4 定位结果

虽然由于第3个传感器的加入满足了三传感器矢量匹配关系，在算法上实现了多尺度下的最佳时延估计，但是由于现场的复杂性及仪器的偶然故障等仍然难免不准确现象的发生.同时由于第3个传感器的加入使得计算出来的结果有了判断的依据.在传统相关法中速度作为已知量输入，因此可以利用对速度的经验了解，来考察定位系统计算结果的准确性.速度如果可信，则可认为式(1)中τ23max是正确的，由于有三传感器矢量匹配关系的约束，τ23max正确又可说明 τ12max、τ31max正确，从而说明系统确实正确捕捉到了泄漏信号，也就校核了整个系统计算结果的准确性.例如在图4所示的真实定位实验中，系统计算出的速度正好在铸铁管道的声传播速度范围内，即可判断此次定位结果可以接受(实际距传感器1的距离为6 m).因此利用三传感器检漏方法可对定位结果进行经验判断，从而避免误检.

2 管道泄漏定位试验

图5为管道泄漏定位试验装置，漏点定位时，首先需要在疑似漏点的两侧按照图1所示的方式安放传感器，进行3路泄漏信号的采集，然后在labVIEW软件平台上实现如图2所示的漏点定位计算.

为了验证三传感器检漏方法的有效性，将其与传统的两传感器相关法在同一条件下试测结果作一比较，在实验室中进行直管段和弯管段的定位结果分析.结果表明，管道弯曲对信号传播有较大的影响.对于两传感器方法而言，由于其没有在多尺度内对真实信号的筛选能力，最终得到的只能是能量最强频带上信号的相关时延计算结果，而这个信号在弯管道上的传播过程中可能已经发生变化，或者被噪声干扰，因此两传感器方法的多数定位结果已经失去了工程应用价值，而三传感器方法是利用三传感器间的匹配关系基于多频带上多组时延结果进行筛选，从而得到一组相对最优的结果.可见，不管是在直管段中还是在弯管段中三传感器方法的定位结果都优于两传感器方法，体现了三传感器方法较好的适应性和稳定性.

上述结果由于在实验室条件下测得，测试距离较短，因此较小的定位偏差，都可能导致较大的误差.同时近距离管道泄漏信号中各种模态来不及衰减，接收到的模态较多且相互干扰［11］，文献［2］也曾提到长距离下的定位结果要好于近距离检测的结果，所以在实际的长距离管道漏点定位中效果会好于实验室结果.

图5 管道泄漏定位试验装置

由于校核距离(传感器2、3之间的距离)的一个重要作用是计算速度，距离越短，对应的时延就越小，对采集和计算设备的要求越高，因此在实际应用中要尽可能地增大校核距离以提高定位的精度.

3 结论

1)第3个传感器的引入，有了一系列针对时延准确求取的保障措施.

2)利用多尺度分析方法，实现了泄漏信号的信噪分离，从而使真实时延结果得以呈现.三传感器矢量匹配筛选，能够将真实的时延结果从众多“假象”中得以提取.

3)第3个传感器的引入，使传播速度的输入更加有针对性，提高了漏点定位精度，适应性更强.

4)本方法采用3个传感器，但实际漏点定位中可以扩展为多个传感器互为校核，既可以增加结果的可信性，又方便实现更大范围内的漏点普查和定位.

［1］GAO Y，BRENNAN M J，JOSEPH P F，et al.A model of the correlation function of leak noise in buried plastic pipe［J］.Journal of Sound and Vibration，2004，277:133-148.

［2］文静.供水管网泄漏检测定位中的信号处理研究［D］.重庆:重庆大学，2007.

［3］PAVIC'G.Experimental identification of physical parameters of fluid-filled pipes using acoustical signal processing［J］.Applied Acoustics，2006，67:864 －881.

［4］GAO Y，BRENNAN M J，JOSEPH P F.A comparison of time delay estimators for the detection of leak noise signals in plastic water distribution pipes［J］.Journal of Sound and Vibration，2006，292:552－570.

［5］孟子厚，盛胜我，赵松龄.自来水管网相关检漏技术中时延估计方法的选择与综合［J］.声学技术，1995，14(1):15－21.

［6］KNAPP C H，CARTER G C.The generalized correlation method for estimation of time delay［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1976，24(4):320－327.

［7］殷恒刚.基于小波变换二次相关时延估计算法的声定位技术及实验研究［D］.南京:南京理工大学，2009.

［8］杨静，文玉梅，李平.自来水铸铁管道泄漏声信号频率特征研究［J］.应用声学，2006，25(1):32 －33.

［9］孙书学，吕艳新，顾晓辉.噪声相关条件下多传声器时延多尺度估计［J］.震动与冲击，2008，20(12):160 -163.

［10］OLSEN L R，CHAUDHURI P，GODTLIEBSEN F.Multiscale spectral analysis for detecting short and long range change points in time series［J］.Computational Statistics and Data Analysis，2008，52:3310－3330.

［11］AHADI M，BAKHTIAR M S.Leak detection in waterfilled plastic pipes through the application of tuned wavelet transforms to acoustic emission signals［J］.Applied Acoustics，2010，71:634 －639.