土石坝渗流计算中的有限元应用研究

华 静，杨华舒

（1.红河学院工学院，云南 蒙自 610000；2.昆明理工大学电力工程学院，云南 昆明 650051）

目前求解渗流场的方法有数值计算方法、模型试验方法和水力学方法。根据水力学和渗流力学理论，通过对工程水文地质剖面的概化，在一些特定条件下可以采用水力学方法对渗流场进行理论求解。由于水力学方法对地层情况的适应性差，过多的地层概化又往往影响计算精度，因此其应用受到很多限制。

渗流场的模型试验方法主要有砂槽模型方法和电模拟方法两种类型。电模拟方法又称导电解质方法（导电液或导电纸等）和电阻网络法。根据目前发展情况，以电阻网络模拟方法较为常用。

渗流场的数值计算方法主要有两种，即有限单元法和有限差分法，以有限单元法最为常用[1,2]。随着计算机和计算技术的快速发展，渗流计算的数值方法和程序日趋完善，功能强大，尤其是有限单元法，基本上可以满足土石坝工程的渗流计算要求，并得到一定的普及。但将有限单元法应用于实际工程渗流计算中还存在一些问题有待研究解决。本文对这些问题进行分析，并探讨解决问题的方法。

1 土石坝渗流及其有限元计算方法

1.1 土石坝的渗流特点

坝体和坝基的渗流控制是保证土石坝安全的一项重要措施。由于填筑土石坝的土料和坝基的砂砾是散粒结构，颗粒间存在大量的孔隙，具有一定的透水性。水库蓄水后，在水压力的作用下，水流必然会顺着坝身土料、坝基土体和坝端两岸地基中的孔隙渗向下游，造成土石坝渗漏。

土石坝渗漏，一般可分为正常渗漏和异常渗漏。正常渗漏的渗漏量较小，水质清澈可见，不含土壤颗粒，对坝体或坝基不会造成渗透破坏。异常渗漏的渗流量较大，比较集中，水质浑浊，透明度低，可使坝体或坝基发生管涌、流土和接触冲刷等渗透破坏。许多土石坝发生严重事故，就是由异常渗漏而引发的。异常渗漏，按其部位可分为坝身渗漏、坝基渗漏、接触渗漏和绕坝渗漏。坝身渗漏的逸出点均在土坝的背水坡面。坝基渗漏，其渗水通过坝基的透水层，从下游坝脚或坝脚以外覆盖层的薄弱部位逸出，会造成坝后管涌、流土和沼泽化。接触渗漏，其渗水从坝身与坝基或岸坡的接触面和坝体与刚性建筑物的接触面通过，在坝后相应部位逸出。绕坝渗漏，其渗水通过两坝端岸坡未挖除的坡积层、岩石裂隙、溶洞和生物洞穴，从岸坡下游侧逸出。

1.2 土石坝渗流的有限元计算方法

有限元方法是按照变分原理，求泛函积分找其函数值，即把微分方程及其边界条件转变为一个泛函极值问题[3]。将有限元应用于土石坝渗流计算的方法如下：

1）定解问题转化。将概化的偏微分方程的定解问题，转化为相应的变分问题。

2）离散化。将求解域划分为具有一定几何形状的单元，进行单元编号，并确定插值函数，对结点进行总体编号和单元上的局部编号。

3）单元分析。以单元结点水头函数值的插值函数，来逼近变分泛函方程中的水头函数，得出单元上以结点水头值为未知量的代数方程组，从而导出单元渗透矩阵。

4）总体渗透矩阵合成。由单元渗透矩阵合成总体渗透矩阵，并以定解条件代入，从而得出整个求解区域上的总体有限元方程。该合成过程，由结点局部编号与总体编号的关系来确定。

5）求解未知水头。求解线性代数方程组，进而求解各结点的未知水头值。

6）结果分析。结果分析及其他相应所需物理量的计算。

这种方法的优点是，能够适应各种复杂的工程地质条件，不需要对地层进行太多的简化，计算精度高，计算速度快，比模型试验方法省时省力。但在实际工程渗流计算应用中还存在诸如渗流自由面迭代、单元格剖分不当、自由面边界条件转化及不同材料交界面渗透系数选取等问题，影响其计算效果。

2 有限元渗流计算应用问题的处理方法

2.1 渗流自由面的迭代

渗流自由面迭代调整过程中会出现渗流自由面假定过高，或非稳定渗流自由面下降范围较大，尤其是渗流自由面穿过非均质层时会造成单元畸形问题。

处理此类问题，可采用丢弃及恢复单元（结点）TY法。当渗流自由面结点的计算水头值小于或等于其下结点的z坐标时，将该点丢弃，改其下结点为渗流自由面结点，形成新的有限元法计算区域，而与原结点有关的单元则不参加计算。同时，当新的渗流自由面结点的计算水头值大于或等于其上结点的z坐标时，将原结点恢复为渗流自由面的点，而与该点有关的单元则又参加计算。但为了单元形态的合理性，丢弃原结点时应将该点的原始坐标值赋还该点；恢复此点时，应将其下结点的原始坐标值赋还。这种处理方法对于复杂边界条件、自由面穿过非均质区、非稳定流自由面变化大及复杂的建筑物形状等情形尤为适用。

2.2 单元格剖分对节点的影响

因单元剖分不适当，自由面调整时出现局部丢点，会引起自由面上所有点不能用光滑相连的折线连接的现象。可在有限元软件程序模块中加入自适应状态，自动调整单元方向克服这一问题。

图1 正常蓄水位下各点压力水头计算图

图2 正常蓄水位下各点比降计算图

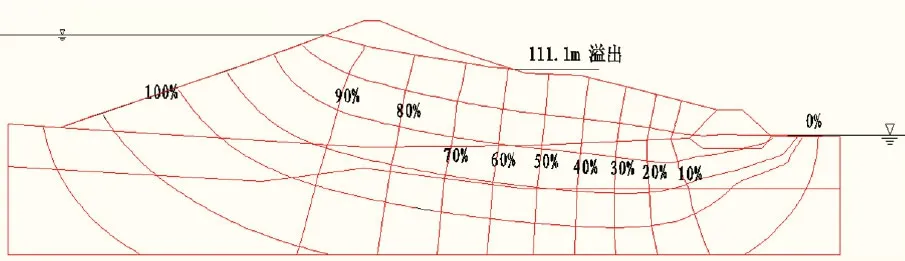
图3 正常蓄水位流网图

2.3 自由面边界条件的转化

对于自由面边界条件的转化问题，采用非饱和一饱和理论，将整个土区域视为渗流区域，根据土的压力与渗透性关系不断修改单元材料性质，而网格不变，根据压力来确定自由面。将自由面边界条件转化为内部求解，使得渗流的偏微分方程的边界条件减少，同热力学偏微分方程及其边界条件相同，可直接采取热分析软件来处理渗流问题。

2.4 不同材料交界面渗透系数的选取

建模取边界条件时，若为均质坝，坝基材料视为同类土料，渗透系数可取为平均值；若为非均质坝体或者处于不同材料交界面，渗透系数取值较困难。对于此类问题，可根据交界面上进入流量和流出流量相等，在交界面S上施加一个差值

3 工程应用

某工程主坝坝身渗水逸出点在下游坝坡110.5m高程处。在坝体钻孔中对坝体土料进行了12段注水试验，渗透系数为1.27×10-2～6.66×10-5cm/s。根据实测浸润线反算出的渗透系数K值，与坝体土料室内实验渗透系数大值均值2.52×10-3cm/s较为接近，说明坝体透水性较强。在不同水位下坝基第三系全风化泥岩的渗透系数为8.93×10-5cm/s，坝基第四系的渗透系数为2.29×10-3cm/s，因此坝体渗流按有限透水地基上的均质土坝分段计算，如图1、图2和图3所示。

将单元格划分为每格2m×2m，采用丢弃单元法对坝体在自由面进行求解。图1中的压力水头值为经过丢弃迭代处理后的自由面。图3中的渗出点与图1的节点一样通过计算来确定其位置，最终确定的渗出点在111.10m处。该渗出点位置经过改善的数值分析计算，从最初的110.50m精确定位在111.10m，为后期做防渗处理提供了准确的依据。

4 结语

采用交界面处理方法可有效解决多种材料坝体的饱和-非饱和渗流问题。采用该方法后，可用常规商用有限元软件较好地解决二维三维饱和-非饱和稳定渗流问题，可以得到较好的结果。但对非稳定渗流问题的计算还有待改进。

[1]陈慧远. 土石坝有限元分析[M]. 南京: 河海大学出版社,1998.

[2]魏宁, 傅旭东, 茜平一. 渗流计算的一种实用方法[J]. 武汉大学学报, 2005, 38(2): 39-43.

[3]朱伯芳. 有限单元法原理和应用[M]. 北京: 中国水利水电出版社, 1998.

[4]杜延龄, 许国安. 渗流分析有限元法和电网络法[M]. 北京: 水利电力出版社, 1992.

[5]张景绣. 坝基防渗与加固技术[M]. 北京: 中国水利水电出版社, 2002.

[6]祁庆和. 水工建筑物[M]. 北京: 中国水利水电出版社,1997.

[7]苏枋, 王建祥, 热依汗. 丢弃单元法在三维有限元渗流分析中的应用[J]. 水力发电, 2009, 35(3): 26-28.

[8]华静. 基于有限元分析的土石坝防渗研究[D]. 昆明: 昆明理工大学电力工程学院, 2006.