含损伤非线性粘弹性本构模型及数值仿真应用①

孟红磊，鞠玉涛

(1.中国航天科技集团公司四院四十一所，西安 710025;2.南京理工大学机械工程学院，南京 210094)

0 引言

固体火箭发动机的装药结构完整性问题一直是制约固体火箭发动机发展的关键因素，为了精确地进行装药结构完整性数值仿真，需要建立精确的本构方程和数值仿真方法。固体推进剂是典型的粘弹性材料，在一定的载荷作用下，表现出非线性粘弹性特性，现有的装药结构完整性分析更多地采用线性粘弹性本构方程［1－7］，而线性粘弹性本构方程与实际误差较大。近年来，非线性粘弹性本构方程发展较快，应用较广的有Schapery非线性粘弹性本构［8－9］、Leaderman 非线性粘弹性本构［10］、微分型非线性粘弹性本构［11］及含损伤的非线性粘弹性本构方程［12－14］。其中，含损伤的非线性本构方程认为非线性是由于材料的内部损伤引起的，能较好地描述材料的非线性粘弹性特性，在沥青混凝土、固体推进剂等方面应用较多。阳建红［12］针对复合固体推进剂建立了含损伤的非线性粘弹性本构方程，彭威［13］针对复合固体推进剂建立了含细观损伤的非线性粘弹性本构方程，但都未针对本构方程进行二次开发和数值计算应用;Hinterhoelzl R M和Schapery R A［14］针对沥青混凝土材料，建立了含损伤的非线性粘弹性本构方程，并进行二次开发，但其本构形式复杂，二次开发难度大，导致计算量大。

本文针对固体推进剂材料，提出了一种新形式的含累积损伤的非线性粘弹性本构方程，并扩展到三维形式，形式简单，便于二次开发，且能较好反映材料的非线性粘弹性本构方程。对装药结构完整性数值仿真提供了精确可行的本构方程及数值方法。

1 本构方程

1.1 弹性粘弹性对应原理

Schapery最初针对弹性材料发展起来的损伤理论，可通过弹性-粘弹性对应原理扩展到粘弹性材料中，通过引入伪应变的概念，将弹性本构中的应变值用伪应变替代后，可变为粘弹性本构方程，伪应变定义为

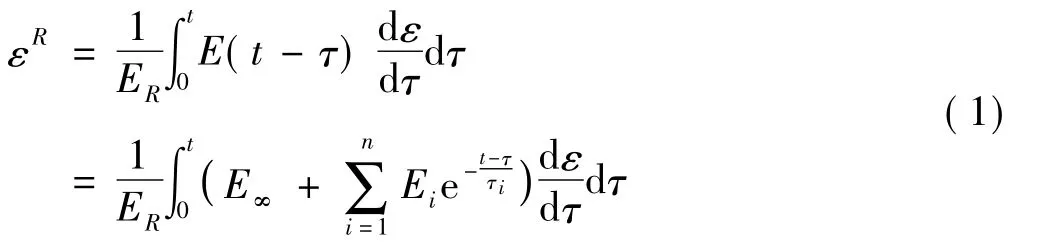
式中ER为参考弹性模量，与弹性模量单位一致，引入参考弹性模量，主要是为了能使伪应变同样是无量纲的，ER可任意选取，通常选取1值或选用材料的初始弹性模量值作为ER。

伪应变是一个卷积分的形式，是一个包含时间遗传因素的量，将伪应变值带入线性粘弹性本构方程后，积分形式的线性粘弹性本构方程变为

式(2)表示的粘弹性本构方程有着与弹性本构方程相似的形式。对于线性粘弹性来说，ER是一个常数，不随着加载过程应变水平的变化而变化。

1.2 含累积损伤的非线性本构方程

当应变值过大时，应力-伪应变曲线出现明显的非线性特性，且不同的加载速率和不同的加载路径时，应力-伪应变曲线并不重合，这说明ER值不仅和加载水平有关，还和加载过程有关。因此，为了能准确描述固体推进剂在较大变形下的力学响应特性，必须建立起ER关于加载过程和加载水平的函数形式。可通过引入损伤因子来准确描述非线性粘弹性，如式(3)所示:

式中 S为损伤内变量，是表征材料内部损伤程度的物理量;C(S)称为软化函数，是关于损伤内变量S的函数;C并不是常数，是一个跟加载过程相关的变量，C值是关于损伤内变量S的函数。

本文结合累积损伤的概念，建立含累积损伤的非线性粘弹性本构方程，并证明含累积损伤的非线性粘弹性本构方程能较好地反映不同应变率条件下及复杂应变率条件下的应力应变响应，含累积损伤的非线性粘弹性本构方程为

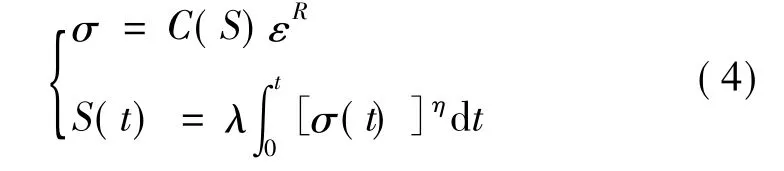
由于改性双基推进剂力学特性不具有明显的方向性，而且在三向应力状态下，材料在未出现明显裂纹之前损伤不具有明显的方向性，在工程中也经常将推进剂力学特性视为各向同性。所以，本文近似认为三维应力状态下，损伤是各向同性的，即损伤内变量S是标量形式，损伤变量S用单一标量表示，那么软化函数C也为标量。

则含损伤的三维粘弹性本构方程表示为

Lai J和hai-Ali Rami M建立的三维非线性粘弹性本构方程中，进行了各向同性假设，其中的非线性系数假设为八面体剪应力的函数［15］。本文基于该思想，假设三维应力条件下，损伤内变量是关于Mises等效应力的函数形式。在三向应力状态下，Mises等效应力常用来判断材料包括固体推进剂材料的屈服，Mises等效应力的水平可衡量材料的损伤软化程度。所以，三维应力条件下，损伤内变量S演化方程中的应力值用Mises等效应力代替。

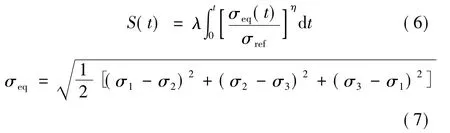
式中 σeq为Mises等效应力。

当单轴拉伸时，σ1=σx，σ2=σ3=0。其中，σx指拉伸方向应力，等效应力可退化为单轴应力形式:

1.3 本构方程参数拟合

含累积损伤的非线性粘弹性本构中，需拟合的有损伤参数λ值和η值，及软化函数C(S)的形式。拟合过程需先通过松弛试验获得松弛模量，然后根据5组等速拉伸曲线，前面损伤变量λ值和η值是先赋初值，λ值可任意选择，一般选为1，η值初值的选择可先选择利用累积损伤模型预测材料损伤时得到的值，具体见文献［16］;在上述给定的损伤变量的情况下，得到的不同速率下的C-S曲线不一定能很好地重合;经过分析，λ值只会影响C(S)函数的拟合结果，不会影响不同速率下C-S曲线的重合性，而η值的选取会影响不同速率下C-S曲线的重合性;所以，λ值就取初始值为最终值，η值需不断调整以获取最优值;根据最终的5组重合较好的C-S曲线，拟合出C(S)的函数形式。根据曲线的形式选择合适的函数形式描述C-S关系，如C(S)=1－aSb的形式。

2 数值仿真应用

2.1 本构方程增量形式及切线模量求解

将通过对含累积损伤的非线性粘弹性本构方程数值展开，来获得应力更新表达式和切线模量矩阵(Jacobian矩阵)。

由主应力 σ1、σ2、σ3求解 Von Mises等效应力，并计算损伤内变量值S。

伪应变由偏伪应变部分和体积伪应变部分组成

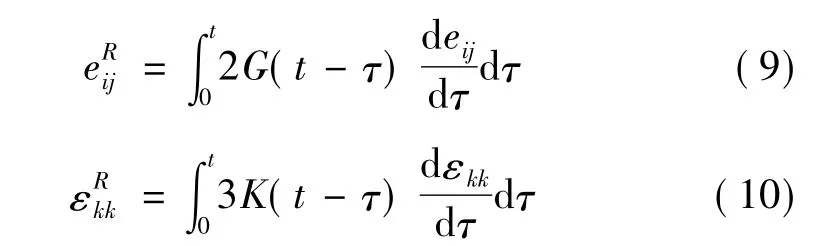
则应力张量分量形式等于

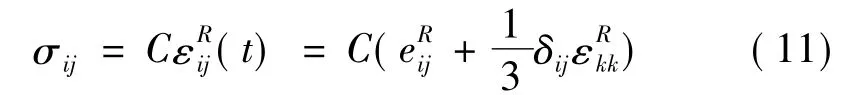
对偏伪应变进行展开，可得到

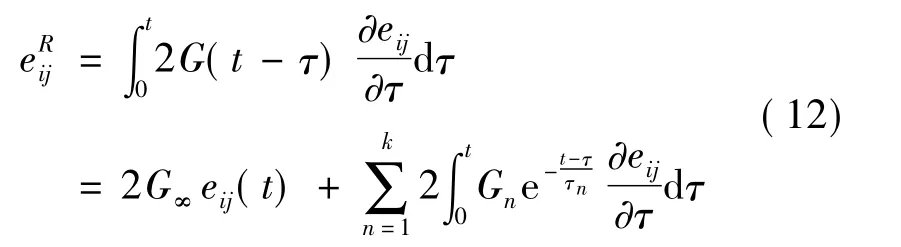
将求和符号中的各项积分分别单独表示。其中，qij，n(t)表示偏伪应变中prony级数中的第n项的遗传积分，qij，∞(t)则表示偏伪应变的稳态项。

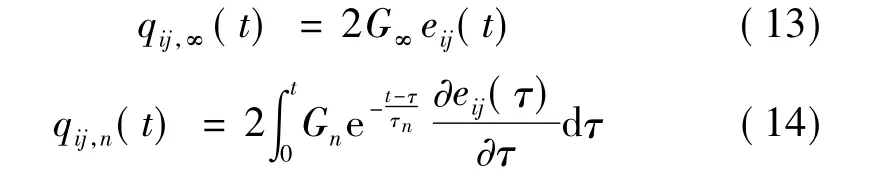
将式(13)和式(14)代入式(12)中，偏伪应变可表示为各项遗传积分之和的形式。

由式(15)可得到t+Δt时刻偏伪应变增量:

同理，体积伪应变展开可得到

将体积伪应变中求和符号内的各个积分项也分别单独表示。其中，qkk，n(t)表示体积伪应变中prony级数中的第n项的遗传积分，qkk，∞(t)则表示偏伪应变的稳态项。

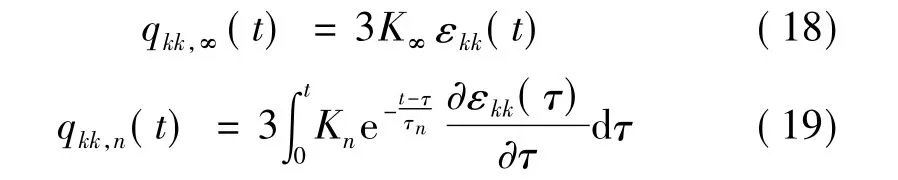
将式(18)和式(19)代入式(17)中，体积伪应变可表示为各项遗传积分之和的形式:

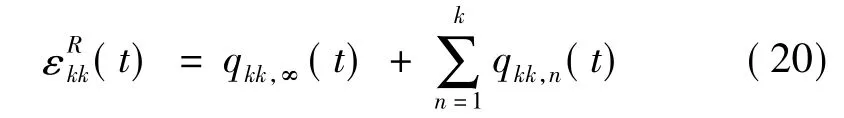
由式(20)得到t+Δt时刻体积伪应变增量:

对损伤内变量S进行离散，可得

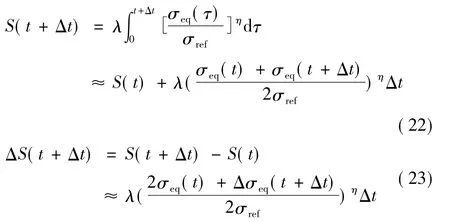
对偏伪应变中prony级数的第n项的遗传积分进行数值离散，将界限(t，t+Δt)内的积分表示为两段积分，第一段是极限(0，t)内积分，第二段是(t，t+Δt)内积分，并将t～t+Δt时间段内的应变率近似为恒值，用平均应变率代替，整理后可得到:

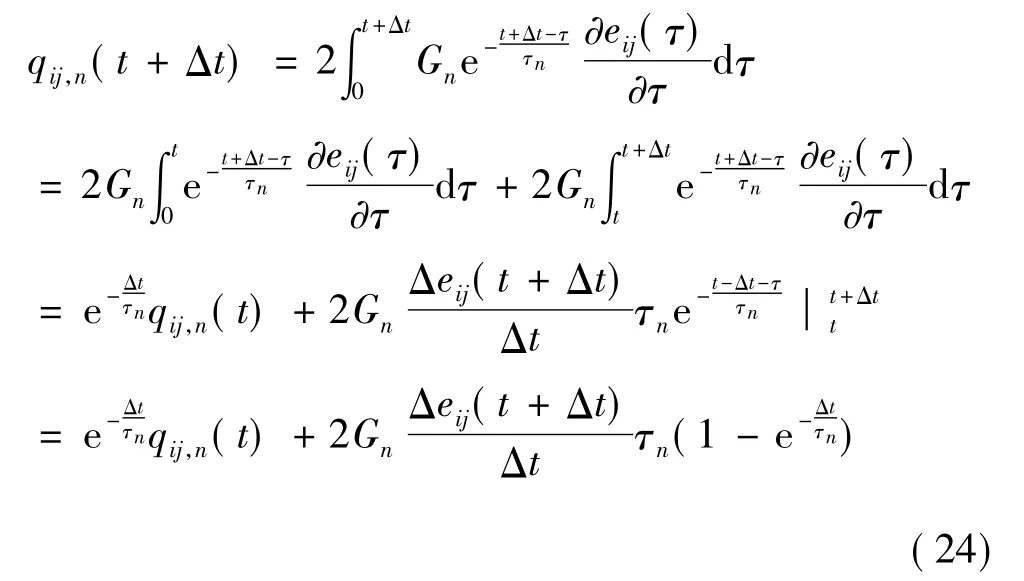
由式(24)得到

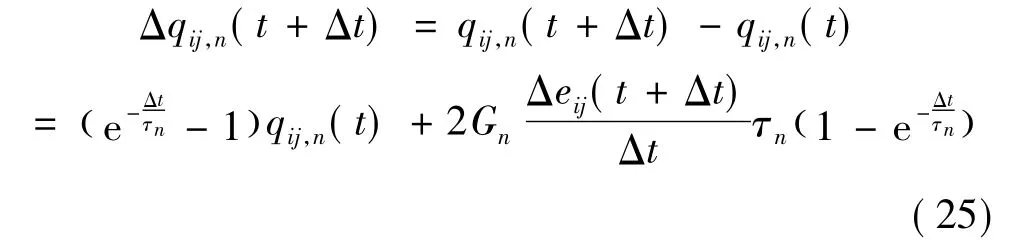
由式(13)得到

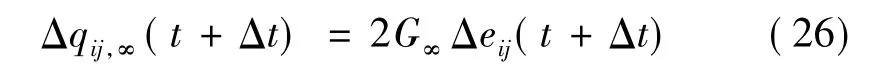
同理，对体积伪应变中prony级数的第n项的遗传积分进行数值离散，整理后可得到:

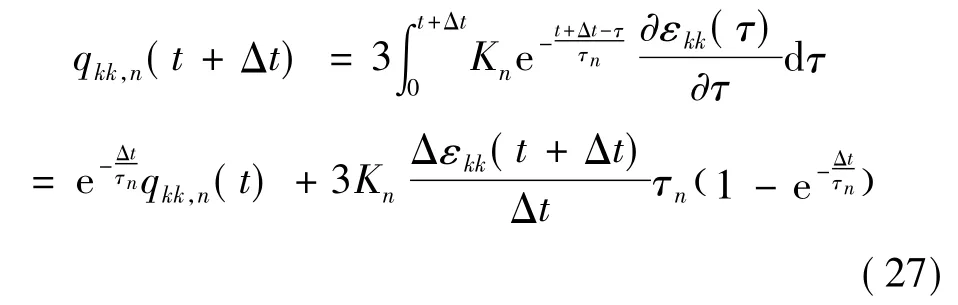
由式(18)得

由式(27)得

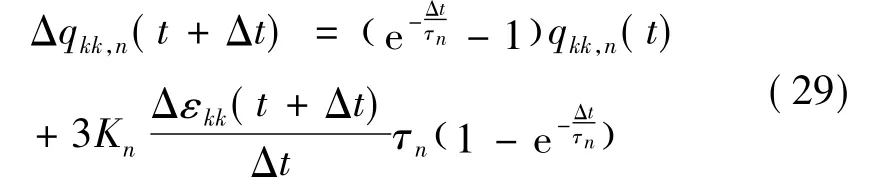
将式(25)和式(26)代入式(16)中，得到偏伪应变增量:

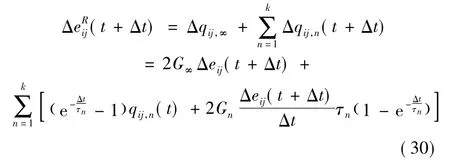
将式(28)和式(29)代入式(21)中，得到体积伪应变增量:

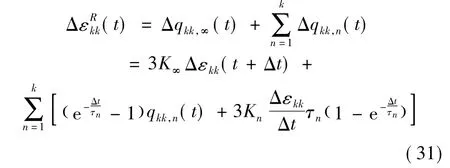
总的伪应变增量可表示为偏伪应变增量和体积伪应变增量之和的形式:

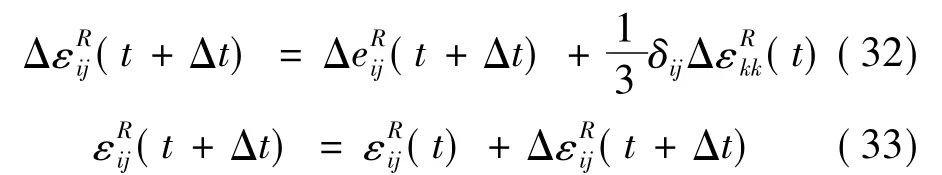
进而可得到

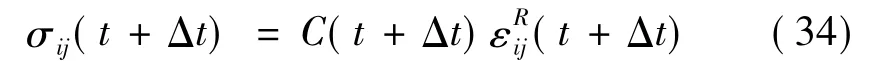
对于粘弹性材料来说，一致切线模量分量形式表示为［14］

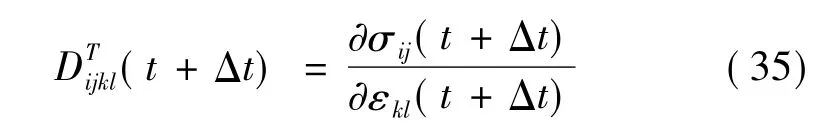
可得出三维时切线模量表达式［14］:

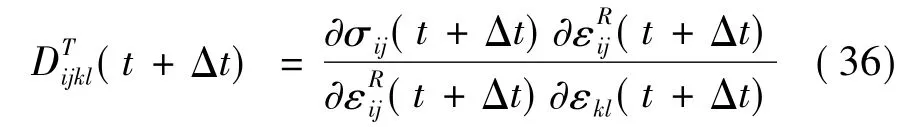
式(36)中认为，粘弹性和损伤对Jacobian矩阵的影响是解耦的。由于软化函数C(S)和损伤内变量是关于Mises等效应力的复杂的函数形式，因此精确的一致切线模量的计算，将是相当复杂并耗费相当多的计算时间，Hinterhoelz.l R M 和 Schapery R A［14］在对其建立的三维含损伤非线性粘弹性本构方程求解一致切线模量时，同样遇到这样的问题，他们在对应力关于伪应变的求偏导时，认为损伤内变量是固定的，即可得到式(36)的结论。由此获得的切线模量并不和应力的更新相一致，相当于割线模量，这样会导致Newton-Raphson迭代过程收敛变慢，但在Hinterhoelzl R M和Schapery R A及本文进行的实际计算中，并没有出现收敛问题，每个增量步一般通过2～4次迭代过程即可收敛。所以，式(36)既能顺利实现Newton-Raphson迭代收敛，又便于应用。Simo和Taylor［17］在1985年针对率相关材料提出了一致切线算子(CTO)的概念，一致切线算子为应力关于应变增量的偏导。Hinterhoelzl R M基于其一致切线算子获得切线模量。

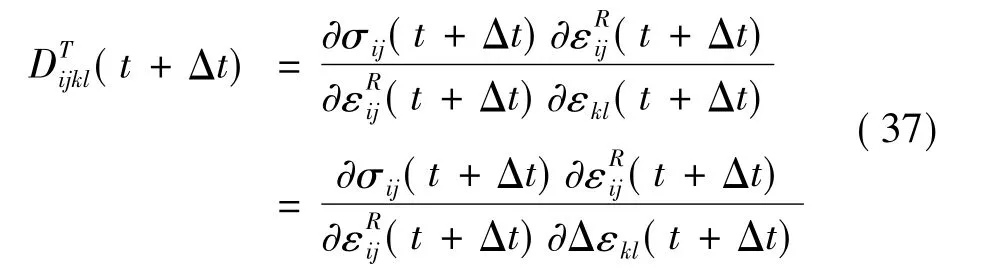
将式(30)和式(31)代入到式(32)中，得到

令

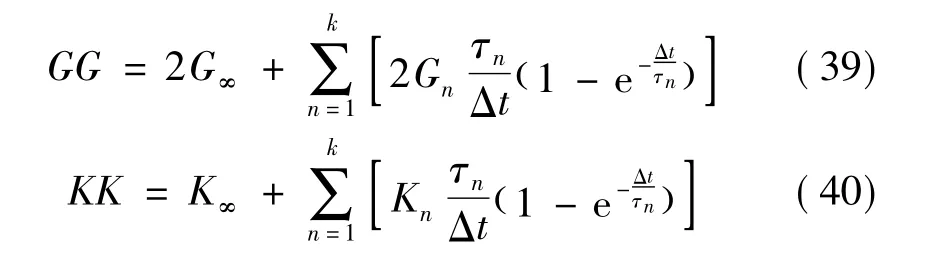
将式(39)和式(40)代入式(38)中，可得

由式(41)可得

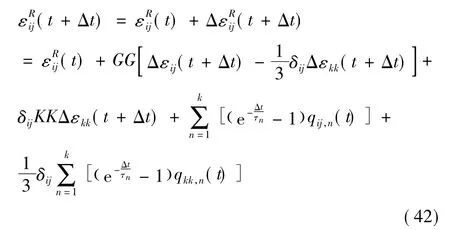
结合式(37)和式(42)可得

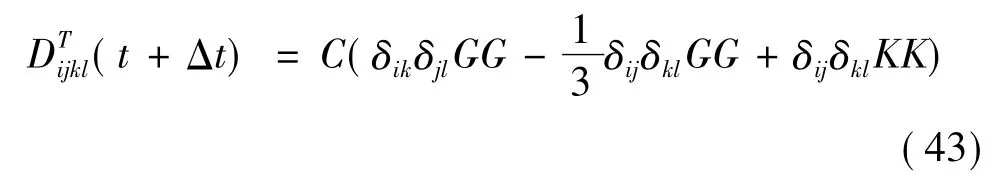
2.2 UMAT子程序介绍

UMAT在配合ABAQUS求解非线性问题时的主要任务:

(1)提供Jacobian矩阵，以便组装切线刚度矩阵，用于迭代求解平衡方程。其中，Jacobian矩阵不影响计算结果的准确性，只影响收敛速度。

(2)提供应力增量和应变增量之间的关系，用于更新应力。

首先在每个增量步开始时，程序给节点外力一个增量，平衡方程不再平衡，ABAQUS会根据上一增量步提供的切线刚度矩阵计算出节点位移变量，然后形成新的刚度矩阵并进行迭代计算，每一次迭代步都需调用UMAT提供的Jacobian矩阵来计算节点位移变量，进而得到节点应变增量，然后再调用UMAT，进而得到应力增量，进行应力更新，积分得到新的内力，如果节点内力和节点外力仍未平衡，继续迭代，直至收敛，获得收敛后的应变增量和应力增量，再通过差值函数得到单元应变和单元应力。至此，该增量步已经完成，进入下一个增量步进行求解计算，UMAT中定义的状态变量也将随之传递给下一个增量步。

2.3 数值仿真及验证

基于改性双基推进剂，获取本构方程参数。利用获取的应力增量表达式和Jacabian矩阵，利用FORTRAN语言编制UMAT子程序，将UMAT子程序代入到ABAQUS有限元软件中，数值模拟等速拉伸过程推进剂材料应力-应变关系，结果如图1所示。理论预测值能较好地预测材料的应力-应变关系。所以，本文建立的含损伤的非线性粘弹性本构方程能较好地用于装药结构完整性分析。

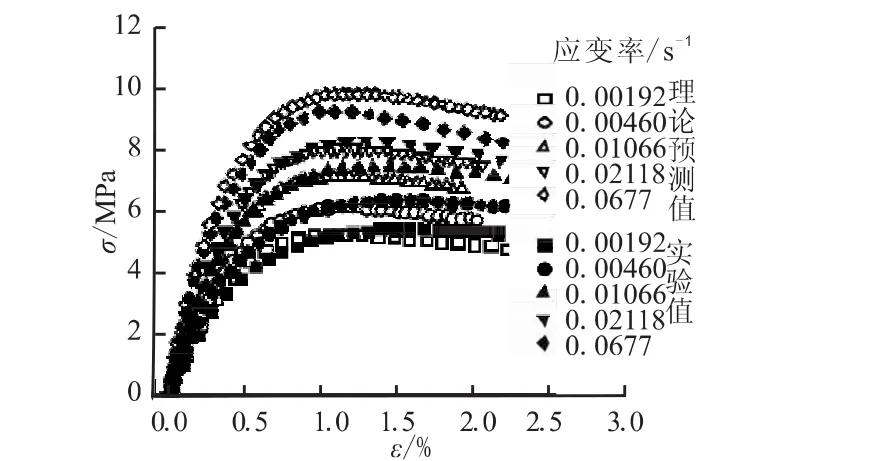
图1 等速拉伸过程应力-应变理论预测与实验对比Fig.1 Comparison between prediction and experimental measurement at constant strain rate tension

3 结论

提出了一种含累积损伤的非线性粘弹性本构方程，并获得其增量形式和切线模量矩阵，结合ABAQUS有限元软件，利用FORTRAN语言编制了UMAT子程序，将本构方程应用到数值仿真中去，并结合试验和数值仿真结果进行对比，验证了该本构方程和数值仿真方法的准确性，为精确的装药结构完整性数值分析提供了本构和方法。本文建立的本构方程没有考虑温度的影响，可在本文建立的本构基础上，通过时温等效引入温度，这样可建立更为精确的本构，其数值离散方法与本文方法近似。

［1］于洋，王宁飞，张平.一种自由装填式组合药柱的低温三维结构完整性分析［J］.固体火箭技术，2007，30(1):34-38.

［2］钟涛，张为华.点火瞬态过程对复合推进剂力学响应特性的影响［J］.国防科技大学学报，2004，26(3):2004.

［3］于胜春，赵汝岩.固体火箭发动机快速升压过程的流固耦合分析［J］.固体火箭技术，2008，31(3):232-235.

［4］隋欣，魏志军.炮射导弹发射过程发动机装药强度分析［J］.弹道学报，2009，21(2):19-22.

［5］Fiedler R，Namazifard A，Campbell M，et al.Detailed simulation of propellant slumping in the TitanIV SRMU PQM-1［R］.AIAA 2006-4592.

［6］Chyuan S W.Dynamic analysis of solid propellant grains subjected to ignition pressurization loading［J］.Journal of Sound and Vibration，2003，268(3):.465-483.

［7］Chyuan S W.Studies of poisson＇s ratio variation for solid propellant grains under ignition pressure loading［J］.Pressure Vessels and Piping，2003，80:871-877.

［8］Schapery R A.On the characterization of nonlinear viscoelastic materials［J］.Polymer Engineering ＆ Science，1969，9:295-310.

［9］Huang Chien-wei，Eyad Masad，Anastasia H，et al.Nonlinearly viscoelastic analysis of asphalt mixes subjected to shear loading［J］.Mech.Time-Depend Mater.，2007，11:91-110.

［10］Leaderman H.Large longitudinal retarded elastic deformation of rubberlike network polymers［J］.Journal of Polymer Science，1962:361-382.

［11］Himanshu Shekhar，Sahasrabudhe A D.Viscoelastic modeling of solid rocket propellants using maxwell fluid moedel［J］.Defence Science Journal，2010，60:423-427.

［12］阳建红，俞茂宏，侯根良，等.HTPB复合推进剂含损伤和老化本构研究［J］.推进技术，2002，23(6):509-512.

［13］彭威，郑坚，白鸿柏，等.复合推进剂微裂纹损伤本构模型研究［J］.固体火箭技术，2003，26(2):33-37.

［14］Hinterhoelzl R M，Schapery R A.FEM implementation of a three-demensional viscoelastic constitutive model for particulate composites with damage growth ［J］.Mechanics of Time-Dependent Materials，2004，8:65-94.

［15］Haj-Ali R M，Muliana A H.Numerical finite element formulation of the schapery non-linear viscoelastic material model［J］.International Journal for Numerical Methods in Engineering，2004，59(1):25-45.

［16］孟红磊，赵秀超，鞠玉涛，等.基于累积损伤的双基推进剂强度准则及实验［J］.推进技术，2011，32(1):109-112.

［17］Simo J C，Taylor R L.Consistent tangent operators for rateindependent elastoplasticity［J］.Computer Methods in Applied Mechanics and Engineering，1985，48(1):101-118.