一种粒子增强体复合材料的线粘弹性模型①
龚建良,刘佩进,李 强
(西北工业大学燃烧、热结构、与内流场重点实验室,西安 710072)
0 引言
粒子增强体复合材料主要是由高聚物为基体的粘结剂和固体颗粒的增强体组成[1]。高聚物基体是连续相,具有粘弹性特性,其力学性能强烈依赖于温度、应变率[2]。另外,粒子增强体复合材料分布着大量的固体颗粒,起到增强作用,固体颗粒的粘性很小,但其杨氏模量比基体要大得多[3]。在外载荷的作用下,由于组分有效性能的差异,导致粒子与基体处应力集中,较易产生界面脱湿[4]。界面脱湿是一个重要的力学行为,但在实验上,一般无法单独分析一种变形特性(如脱湿)对宏观本构关系的影响。为了单独定量分析界面脱湿对粒子增强体复合材料力学性能的影响,对其展开数值模拟是必要的。
目前,国内外针对粒子增强体复合材料的细观力学已存在研究。国内,赵颖华于1999年,针对颗粒增强复合材料,应用细观力学的均质化方法,研究了界面损伤对颗粒增强复合材料弹性性能的影响[5];袁嵩于2006年,针对复合固体推进剂,使用轴对称单胞模型,利用细观力学有限元法,计算了颗粒与基体粘接完好和存在脱粘两种情况下颗粒与基体内的应力分布,分析了复合固体推进剂的细观失效机理[6];陈建康于2003年,针对粒子增强体粘弹性复合材料,使用Eshelby等效理论与Mori-Tanaka法,建立了宏观本构关系,得出了宏观应变率、粒子分散度、基体的松弛时间与界面粘接强度对宏观本构关系都具有重大影响[7]。国外,伊利诺依大学的Tan于2005年,针对PBX 9501高能炸药,使用数字图像相关(DIC)技术,获取了基体与粒子的界面粘性定律,确定了模型参数[8],并在RVE上,使用平均化与Mori-Tanaka法,确定了高三轴应力下的线弹性宏观本构关系,利用有限元技术数值模拟了宏观本构关系,显示了增强体粒子的大小对PBX 9501高能炸药的界面脱湿有重大影响,并得出了临界脱湿粒径[3]。Tan于2008年,在线弹性本构关系的基础上,使用Laplace变换原理,将线弹性宏观本构关系发展到粘弹性的宏观本构关系,但没有考虑脱湿发展的整个过程[9]。
本文依据复合材料细观力学理论与Laplace变换原理,利用Tan等从相关实验中得出粒子与基体的界面粘性模型[8],推出了一种改进的粒子增强体复合材料的三维线粘弹性本构模型,并针对高能炸药PBX 9501展开了有限元数值模拟,探讨了不同温度、常应变率、颗粒粒径和粒子体积分数对粒子增强体复合材料力学性能的影响。
1 粒子与基体的界面粘性模型
Tan等利用数字图像相关算法,从高能炸药PBX 9501的紧凑拉伸实验中,确定了高能炸药PBX 9501粒子与基体的界面粘性模型,如式(1)[8]:
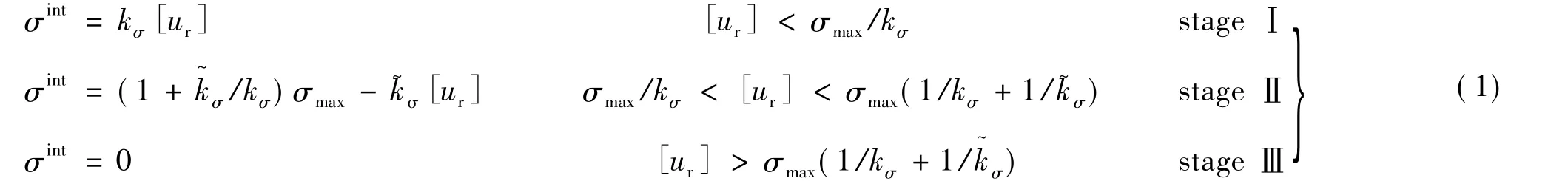
粘性模型由3个阶段组成,分别是弹性上升段、损伤发展段、完全脱湿段,且每段线性分布。它完全决定于参数:粘性强度σmax、线性模量kσ和软化模量
2 粒子增强体复合材料的三维线粘弹性本构关系
为了推出粒子增强体复合材料的三维线粘弹性本构关系。首先,在粒子增强体复合材料中,给定一个代表性体积单元RVE(Representative Volume Element),RVE的体积由基体体积Ωm和粒子体积Ωp组成,记粒子体积分数f=Ωp/Ω。σm和σp分别表示基体和粒子的平均应力,是二阶张量。复合材料的平均应力表示如下[3]:
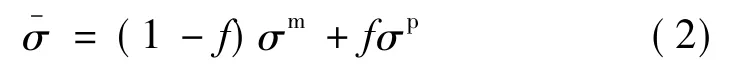
同理,εm和εp分别表示基体和粒子的平均应变。复合材料的平均应变表示如下:

其中,fεint是考虑到粒子与基体的界面形变。εint是按照粒子与基体界面Sint的两边位移之差[u]=um-up来确定,是一个二阶对称张量,表示如下[3]:
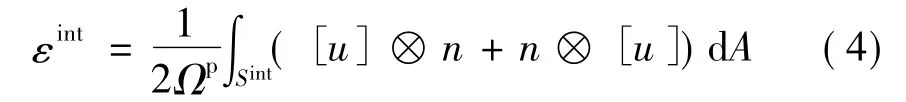
式中 um和up分别表示界面处基体侧和粒子侧的位移;n表示单位法向量,方向指向基体;Sint表示粒子与基体的界面面积。
假定固体颗粒是线弹性与基体是粘弹性的,依据粘弹性理论,分别有本构关系[9]:
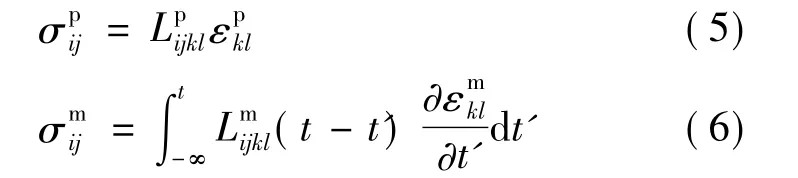
其中
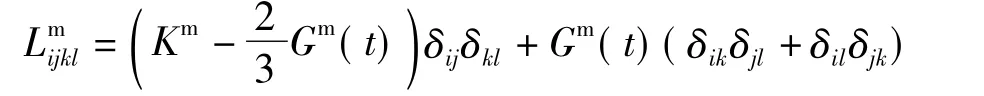
现将基体剪切模量Gm(t)用Prony级数表示[10],即移位因子使用WLF式确定[11],其中参数 T0=19 ℃,C1=6.5,C2=120 ℃[12]。
为了使用弹性与粘弹性的相应原理,需对式(5)和式(6)进行Laplace变换:
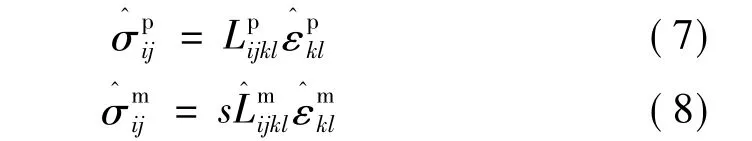
为了在变换后的空间建立本构关系,还需对式(2)与式(3)进行Laplace变换:
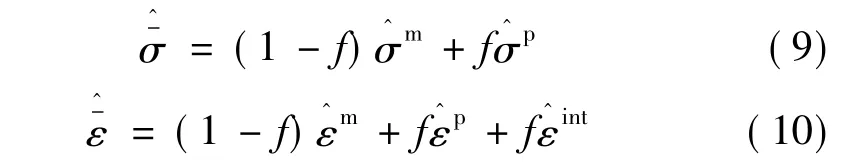
最后,将式(7)与式(8)代入式(10),并使用式(9),可得到变换空间下粒子增强体复合材料的三维本构关系,用应力表达[9]:
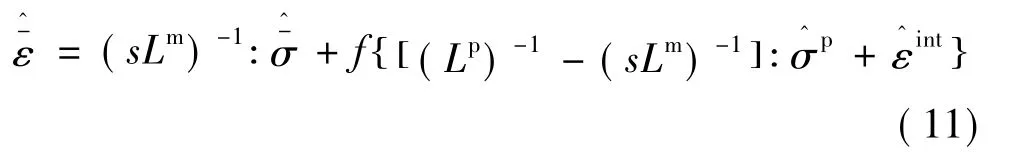
在三轴应力载荷下,使用细观Mori-Tanaka方法,经过理论推导及近似处理,提出了改进的粒子增强体复合材料线粘弹性模型,表示如下:
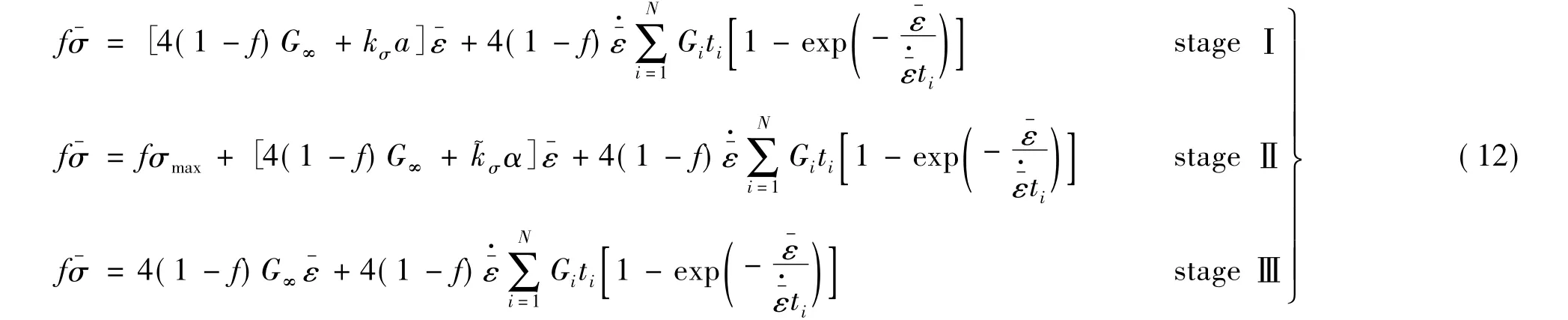
3 数值算例与分析
为了验证本文模型与程序的可靠性,针对高能炸药PBX 9501力学性能,开展了大变形有限元的数值模拟。利用Tan等从高能炸药PBX 9501的紧凑拉伸实验中得到的数据,有 σmax=1.7 MPa,kσ=1.55 GPa/线粘弹性基体的剪切模量用Prony级数表示,系数参考Mas等给出的表1,数据单位 MPa,且 G∞=0[10];线弹性固体颗粒的体积模量14.23 GPa 和泊松比 0.31。

表1 对于高能炸药PBX 9501的Prony级数的系数Table 1 coordination of Prony series with the high explosive PBX 9501
3.1 温度与应变率分别对高能炸药PBX 9501力学性能的影响
为了分析温度与应变率分别对高能炸药PBX 9501力学性能的影响,暂不考虑粒径与粒子体积分数的影响,取粒径a=125 μm,f=60%。首先,在不同温度T=0、25、50℃条件下,施加载荷应变率=2/s,分别得到高能炸药PBX 9501的应力-应变曲线,见图1。可知,随温度的降低,应力-应变曲线往上偏,即应力增大,这是因为随温度的降低而模量升高。其次,在T=25℃的条件下,施加不同常应变率=0.2、2、20 s-1,分别得到高能炸药PBX 9501的应力-应变曲线,见图2。可知,随应变率的降低,应力-应变曲线往上偏,曲线的变化与图1类似,这种现象可利用时间-温度等效原理来解释。当应变率=20 s-1时,要产生 0.5 的应变需0.025 s;当应变率=2 s-1时,要产生 0.5 的应变需0.25 s;当应变率=20 s-1时,要产生 0.5 的应变需2.5 s。所以,达到相同应变的时间缩短,相当于降低温度,粘弹性基体的剪切模量更大,应力应更高。
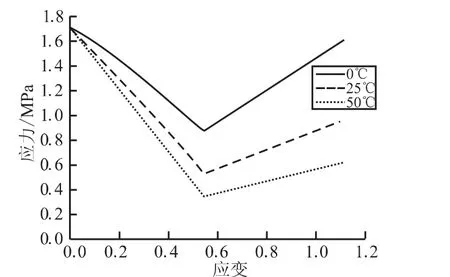
图1 不同温度下的应力-应变曲线Fig.1 Stress-strain relation with different temperatures
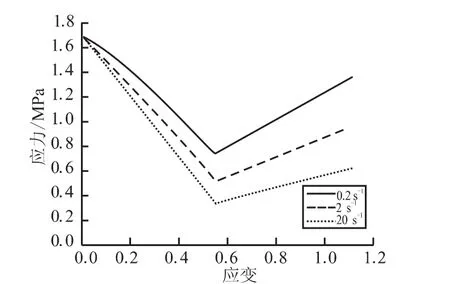
图2 不同常应变率下的应力-应变曲线Fig.2 Stress-strain relation with different constant strain rate
3.2 粒子体积分数与粒径分别对高能炸药PBX 9501力学性能的影响
为了分析固体颗粒粒径与粒子体积分数分别对高能炸药PBX 9501力学性能的影响,将其放置于T=25℃,以常应变率=2 s-1施加载荷。首先,暂不考虑粒径的影响,取粒径a=125 μm,分别得出不同粒子体积分数f=20%、60%、92.7%条件下的应力-应变曲线,见图3。
由图3可知,随粒子体积分数的增大,曲线往上偏,这是因为基体体积分数的减小,粘弹性基体的影响减弱。同时,粒子体积分数较大的复合材料,更易发生界面脱湿[3]。其次,在粒子体积分数f=60%的条件下,分别得出不同粒径α=4 μm和α=125 μm下的应力-应变曲线,见图4。可知,随粒径增大,高能炸药PBX 9501的强度降低,因为粒径大的固体颗粒比粒径小的更易发生脱湿。
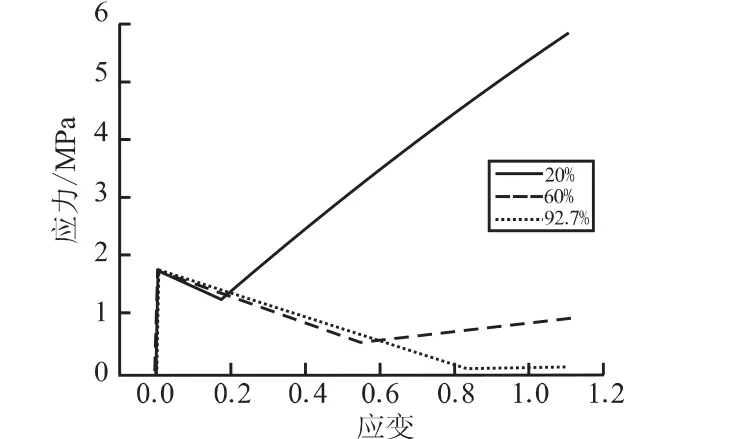
图3 不同体积分数下的应力-应变曲线Fig.3 Stess-strain relation with different particle volume fraction
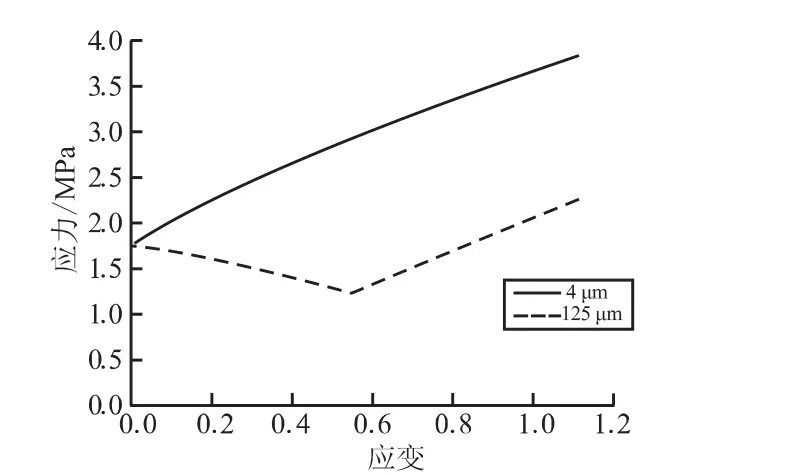
图4 不同粒径下的应力-应变曲线Fig.4 Stress-strain relation with different particle size
4 结论
(1)在高应变率或低温条件下,粒子增强体复合材料具有更高的应力强度。
(2)粒子体积分数越高,粒子增强体复合材料越易发生界面脱湿。
(3)在粒子增强体复合材料中,粒径大的固体颗粒比粒径小的固体颗粒更易发生脱湿。
[1]侯林法.复合固体推进剂[M].北京:宇航出版社,1994:156-256.
[2]张义同.热粘弹性理论[M].天津:天津大学出版社,2002:53-139.
[3]Tan H,Huang Y,Liu C,et al.The Mori-Tanaka method for composite materials with nonlinear interface debonding[J].International Journal of Plasticity,2005,21(10):1890-1918.
[4]陈鹏万,黄风雷.含能材料损伤理论及应用[M].北京:北京理工大学出版社,2006:32-142.
[5]赵颖华.界面损伤对颗粒增强复合材料弹性性能的影响[J].复合材料学报,1999,16(1):117-124.
[6]袁嵩,汤卫红,李高春.复合推进剂的细观失效机理分析[J].固体火箭技术,2006,29(1):48-51.
[7]Chen J K,Huang Z P,Mai Y W.Constitutive relation of particulate-reinforced viscoelastic composite materials with debonded microvoids[J].Acta Materials,2003,51(3):3375-3384.
[8]Tan H,Liu C,Huang Y,et al.The cohesive law for the particle/matrix interfaces in high explosives[J].Journal of Mechanics and Physics of Solids,2005,53(8):1892-1917.
[9]Tan H,Huang Y,Liu C.The viscoelastic composite with interface debonding[J].Composite Science and Technology,2008,68(3):3145-3149.
[10]Mas E M,Clements B E,Blumenthal W R,et al.A viscoelastic model for PBX binders[R].LA-UR-01-3492:2001.
[11]Williams M L,Landel R F,Ferry J D.Temperature dependence of relaxation mechanics in amorphous polymers and other glass forming liquids[J].Journal of American Chemical Society,1955,77(14):3701-3707.
[12]Clements B E,Mas E M.A theory for plastic-bonded materials with a bimodal size distribution of filler particles[J].Modeling and Simulation in Material Science and Engineering,2004,12(3):407-421.

