非均布瞬态内压作用下固体推进剂药柱泊松比随机结构分析①

王君祺，职世君，张建伟

(1.中国空空导弹研究院四所，洛阳 471009;2.航空制导武器航空科技重点实验室，洛阳 471009;3.北京航空航天大学，北京 100191)

0 引言

点火发射是固体火箭发动机所经历的最恶劣的载荷工况。因此，在发动机的设计阶段及后期发动机贮存后的再评估阶段，对固体火箭发动机点火工况下的结构完整性分析就显得格外重要。国内外对固体火箭发动机内压载荷下结构完整性分析的研究较多，但大多采用均匀分布载荷［1－3］，而发动机在实际点火过程中压力波的传递，使得发动机内压力载荷存在瞬态分布特性［4］。因此，若采用瞬态分布压力进行分析，则更接近发动机的实际工况。

由于固体发动机装药受制造、工艺、测量等因素的影响，使得药柱力学性能参数不可避免具有一定的分散性。如泊松比接近于0.5，通过实验很难测定其准确数值，多次的测量结果呈概率分布，具有随机性［5］。若采用确定性的分析方法，得出的结果可信性较差。近年来，随着计算机计算能力的不断提高，为了能描述工程结构的实际情况，考虑不确定性因素已成为一种趋势［6］。因此，有必要对推进剂药柱结构进行不确定性分析［7］。

本文首先采用Abaqus商用有限元软件计算了固体火箭发动机点火过程压力瞬态分布时装药的结构完整性，然后结合粘弹性有限元法和Monte-Carlo方法，即构成所谓的粘弹性Monte-Carlo方法，考虑了泊松比随机分布对固体火箭发动机点火过程装药结构完整性的影响。

1 物理模型和计算方法

1.1 发动机模型及网格划分

发动机的构成主要有壳体、绝热层和药柱，假设药柱和绝热层为线粘弹性材料，壳体为弹性材料。线粘弹性本构关系为

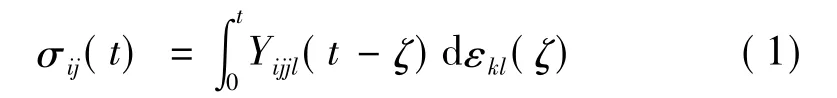
式中 Yijkl(t)为四阶张量，具体材料参数参见文献［8］。

发动药柱为管状结构，考虑发动机几何构型的对称性，取其1/4建模，如图1(a)所示。其中，面1为点火药包瞬间压力填充区域，面2的压力符合式(3)的分布。采用六面体单元对发动机进行网格划分，如图1(b)所示。

图1 固体火箭发动机1/4模型及网格划分Fig.1 SRM 1/4 model and mesh

1.2 发动机瞬态载荷及药柱泊松比分布

1.2.1 发动机瞬态载荷分布

发动机点火药位于发动机头部，点火后，发动机燃烧室药柱头部压力急剧增加，并以很快的速度向燃烧室尾部传播。在此期间，发动机内压力载荷呈典型的非均布和非稳态特征。文献［4］中提出的固体火箭发动机点火过程内压瞬态非均布函数，即

式中 p0为平衡压强;v为压力轴向传播速度;z为轴向坐标;t为发动机点火时间;a为压力增长速因子。

当点火药被引燃后，压力会瞬间充满发动机头部区域，若直接采用上述公式，发动机燃烧室压力分布为从z=0位置开始递减，与实际情况有所出入。因此，假定发动机头部点火药部位在增压过程中压力保持一致，即在式(2)中引入发动机头部点火距离的参数b，则式(2)可改写为

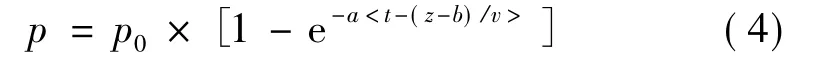
文中分别取 a=500，b=45 mm，v=50 m/s，发动总长为500 mm。

1.2.2 药柱泊松比随机分布

采用Monte-Carlo法进行结构随机有限元分析时，首先要根据随机变量的已知概率分布进行抽样，然后再对每个抽取的样本，利用有限元法求取发动机药柱的结构响应量，最后根据所有样本的计算结果进行统计分析。对随机变量进行抽样时，若采用直接Monte-Carlo方法，则在不改变抽样的均值和方差的前提下，样本数目巨大，由其对于三维粘弹性药柱的有限计算，其计算量太大。因此，为提高粘弹性Monte-Carlo随机有限元的计算效率，采用Latin超立方抽样技术，该方法在不改变抽样的均值和方差的前提下，可有效减少样本数目。

在对固体火箭发动机装药点火工况下的结构完整性进行分析时，泊松比的影响往往较大［9］。考虑药柱泊松比为随机参数，对泊松比进行随机抽样。泊松比的分布采用截断型高斯分布，相关参数如表1所示。

表1 药柱泊松比随机分布参数Table 1 Random distribution parameters of Poisson＇s ratio

根据表1数据，对泊松比进行Latin超立方抽样300次，其均值随抽样次数的变化，如图2所示。从图2中可看出，当抽样300次时，其均值已趋于平稳，说明对泊松比进行300次抽样，满足固体火箭发动机装药结构完整性随机分析的要求。

图3所示为泊松比随机分布的统计结果，图形与截断型高斯分布十分接近，这也说明抽样次数是足够的。

图2 药柱泊松比均值随抽样次数的变化曲线Fig.2 Curve of mean of Poisson＇s ratio vs number of sampling

图3 药柱泊松比随机抽样柱状分布图Fig.3 Random sample histogram of Poisson＇s ratio

2 计算结果与讨论

2.1 药柱受非均布内压的计算结果及分析

利用三维粘弹性有限元法，计算发动机在瞬态非均布压力作用下的结构完整性。取5个时间点为研究对象，其压力分布如图4所示。固体火箭发动机的Mises等效应变分布如图5所示。

从图5中可看出，点火过程中不同时刻发动机的Mises等效应变分布。当点火药被引燃后，发动机头部瞬间充满气体，压力增大。如图5(a)所示，在发动机药柱头部产生了较大的应变。

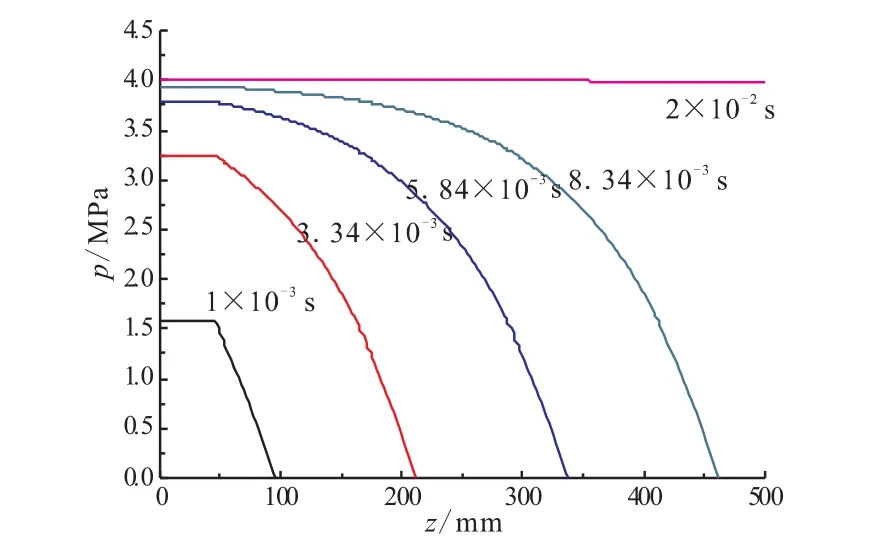
图4 不同时刻发动机压力分布图Fig.4 Distribution of pressure at different times

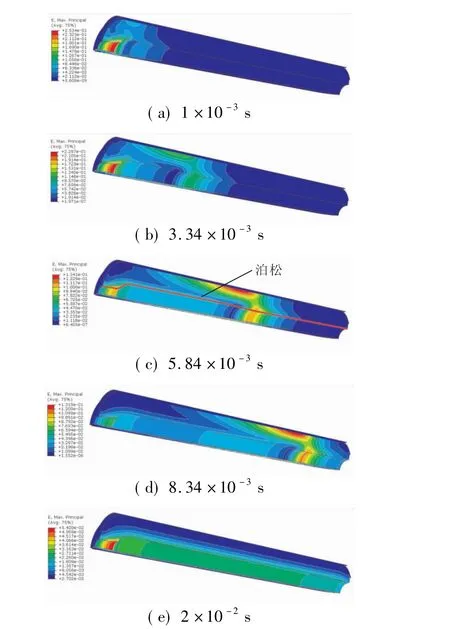
图5 压力传播过程Mises等效应变分布Fig.5 Distribution of Mises strain during pressure diffusion

由于本文忽略了发动机的脱粘处理，因此发动机头部的计算结果存在一定误差，本文主要考虑发动机圆管段在压力传播过程的Mises等效应变分布。随时间增加，压力逐渐向发动机尾部传播。从图5中可明显看出，发动机药柱上存在应变峰的移动。当发动机内部压力趋于稳定时，发动机药柱的应变分布亦趋于稳定。对比图5中的计算结果可知，在压力传播过程中，发动机药柱的最大Mises等效应变值比整个发动机内部压力分布稳定时的最大Mises等效应变值大许多。可见，若采用发动机内部均匀压力分布计算发动机点火过程的结构完整性是不妥当的。

在压力传递的过程中，发动机药柱的受力状态是复杂的。为研究发动机在点火过程药柱的复杂受力状态，取5.84×10－3s时的发动机为研究对象，如图5(c)所示。建立路径并统计路径上节点的轴向应变和Mises等效应变分布，如图6所示。从图6中可看出，沿路径分布的Mises等效应变在压力传播到的位置附近存在明显的波峰和波谷。轴向应变分布是导致这一现象的一个主要原因，在压力传播的过程中，药柱受到发动机头部和尾部壳体的约束，使得药柱圆柱段受到内压载荷作用的部位轴向受拉，而未受到内压载荷的部位轴向受压。药柱头部由于过渡圆弧的结构，在受发动机工作压力作用时，其过渡圆弧处受压。因此，可从图6的轴向应变分布曲线中看出存在两个明显的波谷，分别位于药柱头部和药柱圆柱段。最大Mises等效应变的位置基本上与轴向应变负向最大值的位置一致，即出现在药柱轴向受压最大的位置。由于发动机药柱从受拉状态到受压状态存在一个过渡阶段，即在发动机药柱受拉段和受压段存在一区域的轴向应变接近零，该区域的Mises等效应变很小。因此，在最大Mises等效应变位置之前呈现波谷状分布，这从图6中可明显看出。

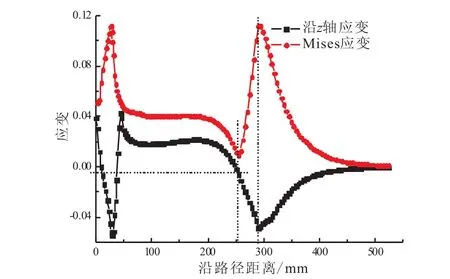
图6 5.84×10－3s时刻发动机路径上应变分布Fig.6 Strain along SRM path at 5.84 ×10 －3s

以发动机中间部位的节点14 639为对象，研究发动机药柱固定点在内压载荷传递过程中的受力状况，如图7所示。

图7 节点14 639 Mises等效应变随时间变化曲线Fig.7 Mises strain-time curve of note 14 639

从图7中可看出，在0.005 5 s时，节点的Mises等效应变达到最大值。因为此时发动机药柱的Mises应变峰刚好移动到节点14 639处，当应变峰继续往发动机后端移动时，节点的Mises等效应变迅速变小，在0.006 3 s时，节点位置刚好处于如图6中所示的Mises应变波谷，此时节点的等效应变最小，随应变峰的继续移动，节点的Mises等效应变逐渐增加，最后趋于稳定。

2.2 药柱随机有限元计算结果及分析

为考虑泊松比对点火工况下发动机药柱结构完整性的影响，采用如图2所示的泊松比随机分布数据，对发动机在瞬态压力分布作用下进行有限元计算，共300个算例。仍以节点14 639为研究对象，统计应变峰经过该点时的Mises等效应变，即该节点在点火过程中的最大Mises等效应变，其柱状分布图如图8所示。

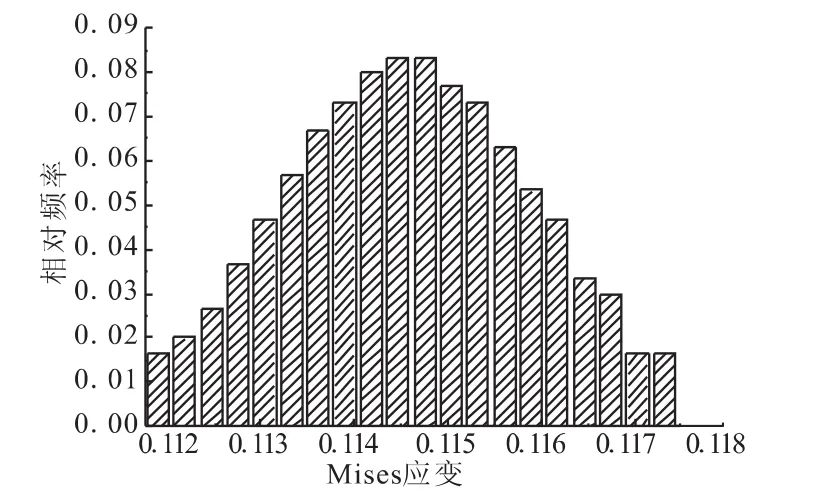
图8 药柱节点14 639最大Mises应变柱状分布图Fig.8 Mises strain maximum histogram of note 14 639

药柱节点14 639最大Mises应变随机分布统计参数如表2所示。从表2中可看出，该节点统计的Mises应变最大值和最小值相差仅0.571 16%。根据节点应变均值和标准差可知，其变异系数为1.104 6%。可见，在瞬态非均布载荷的作用下，泊松比的随机分布对发动机Mises等效应变的影响较小，这与采用均布载荷计算的结果有明显差异。

表2 药柱节点14 639最大Mises应变分布参数Table 2 Distribution parameters of Mises strain maximum of note 14 639

节点14 639的最大Mises等效应变随药柱泊松比的变化，如图9所示。从图9中可看出，泊松比越大，Mises等效应变值越大，且呈线性分布。这与均布载荷下的所得到的结论完全相反。这主要与瞬态非均布载荷的作用下药柱复杂的受力状态有关。因此，不能直接认定泊松比越大，Mises等效应变值就会越小，应充分考虑发动机点火过程的压力传播对药柱结构完整性的影响。

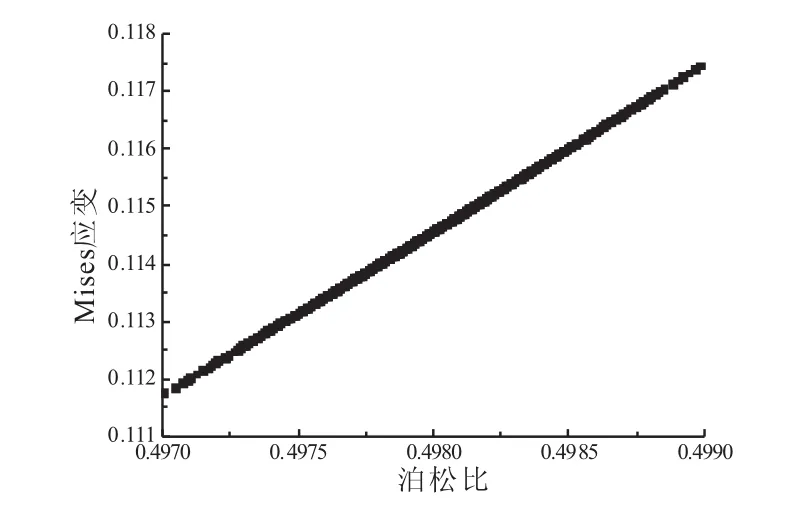
图9 药柱节点14 639的最大Mises等效应变随泊松比的变化曲线Fig.9 Mises strain maximum-Poisson＇s ratio curve of note 14 639

3 结论

(1)固体火箭发动机药柱在瞬态非均布载荷的作用下，其受力状态十分复杂。在点火过程中，发动机药柱上存在应变峰的移动，且计算得到的Mises等效应变远大于均布载荷的计算结果。

(2)算例中药柱泊松比的随机分布对发动机药柱在瞬态非均布载荷作用下的结构完整性影响不大，Mises等效应变的变异系数仅为1.104 6%，且Mises等效应变随泊松比的增大而增大，呈线性分布。而在均布载荷下的泊松比的影响往往较大，且Mises等效应变随泊松比的增大而减小。可见，在瞬态非均布载荷与均布载荷下的结论差别较大，采用均布载荷计算药柱应变，并将其计算结果作为结构完整性分析的依据有其局限性。因此，在对固体火箭发动机结构完整性分析时，应充分考虑发动机点火过程的压力传播过程，即压力的瞬态非均匀分布。

［1］Finne S，Futsaether C，Botnan J.Three-dimensional analysis of solid propellant grains using a nonlinear viscoelastic model［R］.AIAA 1990.

［2］Shiang-Woei，Chyuan.Dynamic analysis of solid propellant grains subjected to ignition pressurization loading［J］.Journal o f Sound and Vibration，2003:465-483.

［3］钟涛，张为华.点火瞬态过程对复合固体推进剂力学响应特性的影响［J］.国防科技大学学报，2004，26(3):7-10.

［4］孟红磊，周长省，鞠玉涛，等.非均布瞬态内压作用下星孔药柱应力分析［J］.固体火箭技术，2010，33(3):289-293.

［5］张海联，周建平.固体火箭发动机药柱随机结构分析及其相关函数研究［J］.固体火箭技术，2001，24(4):25-28.

［6］张海联，周建平.固体推进剂药柱泊松比随机粘弹性有限元分析［J］.推进技术，2001，22(3):245-249.

［7］田四朋，唐国金，李道奎，等.固体推进剂三维粘弹性Monte-Carlo随机有限元法［J］.强度与环境，2007，34(2):51-57.

［8］职世君，孙冰，张建伟.考虑泊松比的固体发动机装药贮存寿命预估［J］.固体火箭技术，2011，34(5):593-597.

［9］Huang-Ta Chu，Jung-Hua Chou.Poisson ratio effect on stress behavior of propellant grains under ignition loading［J］.Journal of Propulsion and Power，2011，27(3):663-668.