超燃冲压发动机变结构进气道设计①

王 青，谷良贤，龚春林

(西北工业大学航天学院，西安 710072)

0 引言

随着航天技术的发展，现代战争对高超声速飞行器加速性、快速性等提出了更高要求。为此，发动机必须能在大马赫数、攻角范围内高性能可靠工作。然而，传统的发动机进气道都是基于单一设计点的优化，不能满足大范围高性能工作要求。因此，发动机变结构设计成为必然。目前，已有学者对变结构发动机进行了有意义的探索研究，文献［1］在超燃冲压发动机研究中提出了发动机下底面可上下、前后移动的变结构方案;文献［2］在文献［1］基础上增加了燃烧室第二扩张角变结构;文献［3］提到进气道可变和燃烧室可变2种变结构方案;文献［4］采用了进气道唇板可上下、前后移动的变结构方案。这些变结构研究大多是基于单目标的设计优化，而对发动机进气道起动等设计要求，决定了超然冲压发动机进气道设计是一个多目标优化问题［5－6］，基于单目标的变结构优化设计不一定满足进气道起动等要求。

本文基于多目标优化，对一种进气道楔形面转折角、进气道高度及唇板长度和角度均可变的变结构进气道进行设计研究。首先，采用遗传算法在设计点下对进气道进行多目标优化，得到Pareto非劣解;然后，以Pareto非劣解中一组可行解为基准，优化得到不同马赫数和攻角下的变结构进气道;最后，通过曲线拟合得到进气道随马赫数和攻角变化的变结构调节规律。

1 优化设计模型

1.1 进气道设计模型和变结构方案

进气道压缩面数目越多，产生的激波系中斜激波数目越多，压力损失越小，但进气道外壳的扩散程度也越大，最终造成较大的外部激波阻力。在压力损失、激波阻力和进气道外壳扩散程度之间权衡，本文选用5楔形体混压式进气道，其中外压段3个楔角，内压段2个楔角，如图1所示。在设计情况下，要求进气道外压段3道斜激波交汇于外缘唇口前缘D点，内压段2道斜激波交汇于上壁面转折点C。

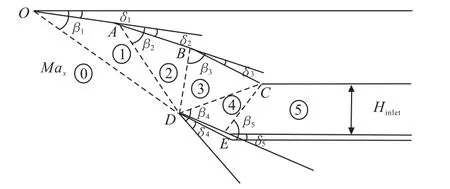
图1 内外混压式进气道设计模型Fig.1 Sketch map of mixed compression inlet

发动机变结构设计相比于固定结构会增加结构复杂性和质量，故一般只对进气道或燃烧室进行结构微调。本文采用单自由度变结构方案，具体是保持楔形面OA、AB、BC长度和转折角δ1不变，自由调节转折角δ2大小，同时根据几何约束条件、转折角和激波角关系，改变转折角δ3、δ4和 δ5大小，唇板ED长度，进气道高度Hinlet，使得激波打到唇口，实现不同马赫数和攻角下发动机高性能工作。δ3、δ4、δ5、ED 和 Hinlet求解公式如下:

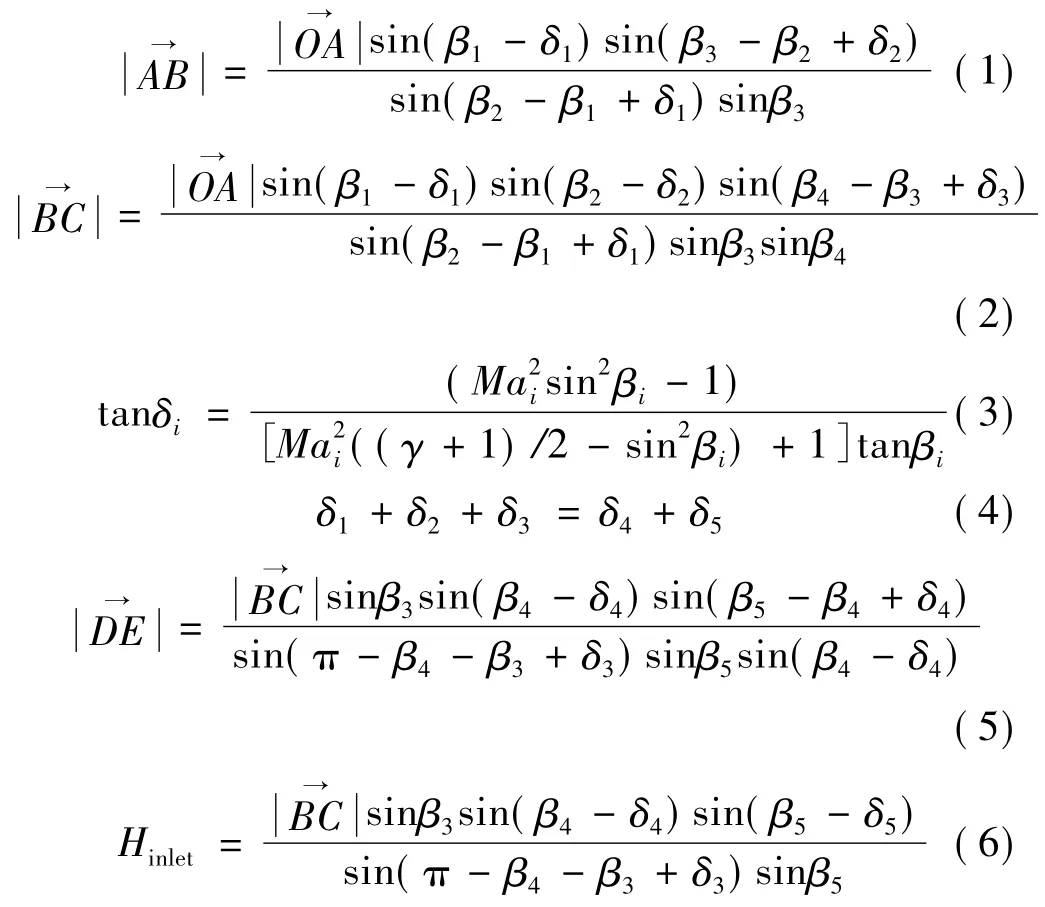
式中 βi为激波角，i=1，2…，5;Hinlet为进气道出口高度。

1.2 目标函数和优化变量

在发动机进气道设计中［7－9］，可选性能指标有总压恢复系数、压升比、空气捕获流量、总压恢复系数方差和阻力系数，优化时希望前3个参数越大越好，后2个参数越小越好。考虑各个参数对发动机性能的影响程度，本文选取进气道出口处的总压恢复系数σ，压升比Pr和阻力系数Cd为目标函数，外压段3个转折角和内压段2 个折角 δi(i=1，2，3，4，5)为设计变量，约束条件为进气道出口静压p5≥1.013×105Pa，且转折角满足 δ1+δ2+δ3=δ4+δ5。则多目标优化模型可描述如下:

目标函数:{－σ，－Pr，Cd};

约束条件:p5≥1.013 ×105Pa，δ1+δ2+δ3=δ4+ δ5，δimin≤δi≤δimax;

设计变量:δi(i=1，2，3，4，5)。

由斜激波Rankine-Hugoniot关系，确定各道斜激波后的气流参数，进而可求出整个激波系的总压恢复系数和压升比。在进气道阻力求解时，为简化计算，将进气道外压缩面上气动载荷在机身轴向的分量近似为进气道阻力，并根据图1进行一维分析，则阻力系数可近似表示为

式中 下标0的量表示自由流场参数，pi(i=1，2，3)为外压段各道斜激波后的静压。

1.3 变结构进气道设计工况

超燃冲压发动机一般要求工作在Ma=2.5～8。此外，考虑大攻角下进气道性能下降非常严重，要求进气道小攻角范围工作。本文在基准进气道设计时，选取飞行高度25 400 m，飞行马赫数8，设计攻角0°为设计点，在进气道变结构设计中，以Ma=3～8、攻角－3°～2°为变结构进气道设计范围。变结构进气道设计基本流程见图2。

图2 变结构进气道设计流程框图Fig.2 Design flow chart of variable inlet

2 基准进气道优化

在基准进气道设计中，根据捕获流量要求，取唇口距头部(O，D点)的竖直距离2.5 m。用遗传算法［10］进行多目标优化，种群个体规模200个，最大进化代数200代，交叉概率 0.9，变异概率 0.25，交配池规模300。优化得到的Pareto最优前沿面如图3所示。

图3 Pareto非劣解Fig.3 Pareto solutions

图3给出的Pareto，每个解都有相同的Pareto等级，在没有引入其他决策信息之前，不能判断解的优劣性，这正体现了多目标优化问题的特点。在σ、Pr和Cd之间进行权衡，选取Pareto非劣解中的一组解作为优化结果，得到基准进气道几何外形尺寸为:楔形面转折角 δ1=6°，δ2=7°，δ3=8°，δ4=10°，δ5=11°;楔形面长度:进气道性能参数:σ =0.593 9，Pr=158.98，Cd=0.141;进气道出口静压 p5=0.375 MPa，满足约束条件。

3 进气道变结构设计

在进气道变结构设计时，按照结构变形方案，取转折角 δ2为设计变量。另外，3个转折角 δ3、δ4和 δ5分别按照几何关系和约束条件计算得到。仍取σ、Pr和Cd为目标函数，采用多目标遗传算法优化求解。此时，种群规模100个，最大进化代数500代，交叉概率0.9，变异概率 0.25，交配池规模 150。

以上文得到的基准进气道为基础，选择马赫数Ma=4，6，7，8，每个马赫数下在攻角 －3°、－1°、0°、1°分别进行变结构优化设计。

优化结果见表1(每种状态优化得到1组Pareto非劣解，根据进气道具体设计要求在3个性能指标间权衡，对每种状态给出1组非劣解)。

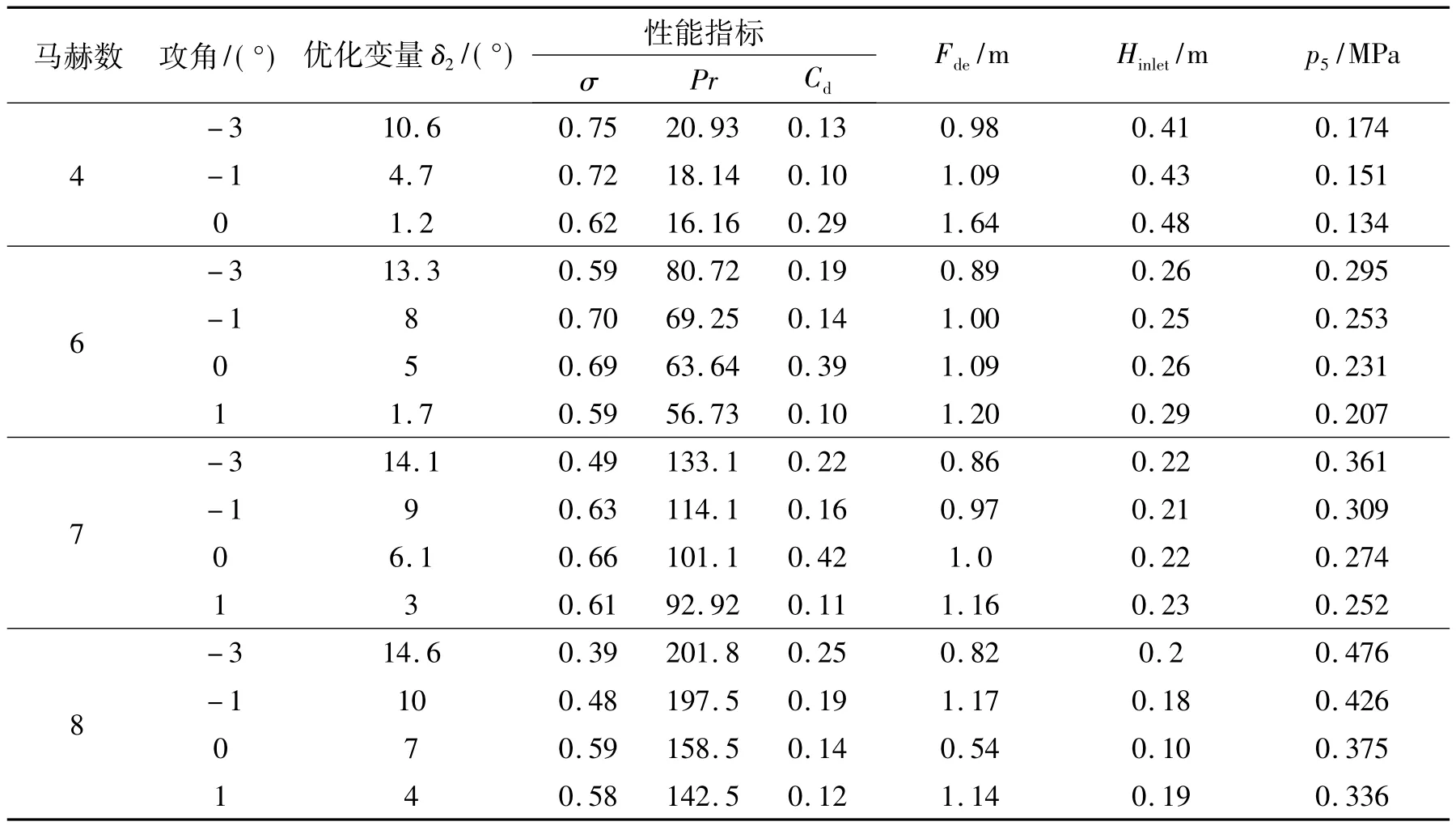
表1 不同马赫数和攻角下优化得到的Pareto非劣解Table 1 Pareto solutions at different Mach numbers and angles of attack

限于篇幅，图4只给出了部分状态的Pareto最优前沿面。图5是攻角0°、不同马赫数下性能最优的进气道变结构示意图，图6是马赫数8、不同攻角下性能最优的进气道变结构示意图。

由表1可知:

(1)通过进气道结构调节，总压恢复系数总体维持在较高水平，且随着马赫数的降低呈增大趋势。

(2)压升比和阻力系数总体上随马赫数减小而降低，进气道出口静压也随之降低，说明随马赫数降低，气流压缩率下降，但进气道出口静压仍满足约束条件。

图4 Pareto最优前沿面Fig.5 Pareto solutions

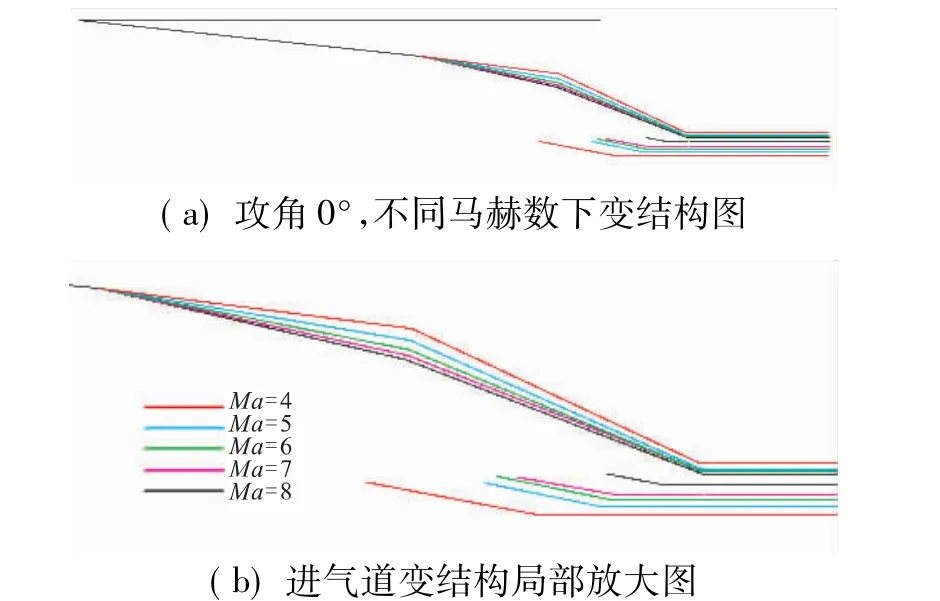
图5 攻角0°下进气道变结构Fig.5 Variable inlet for different mach numbers at δ =0°

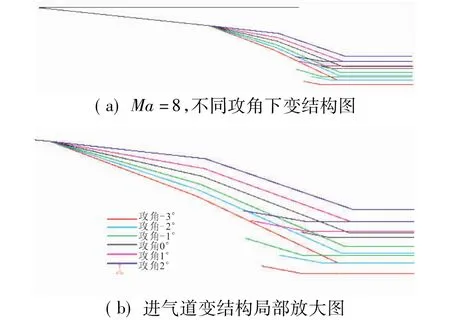
图6 Ma=8下进气道变结构Fig.6 Variable inlet for different angles of attack at Ma=8

(3)进气道高度随马赫数下降而增大，喉道面积增大到低马赫数下进气道正常起动所需面积，实现了低马赫数下进气道的正常起动。

由图5可知，δ2随马赫数的减小而减小，使得进气道上壁面升高，下底面下降，导致进气道高度增加，这和亚燃模态Hinlet取值大而超燃模态Hinlet取值小的要求相吻合。此外，进气道下底板前伸，唇口挡板一方面伸长，一方面转动，以保证激波刚好打到唇口。

分析图6可得，δ2随攻角的减小而增大，使得进气道上表面随攻角减小而下降，下底面也下降，其结果是进气道高度不断减小，这说明小攻角下进气道起动所需喉道面积小于较大攻角下所需喉道面积。随攻角减小，唇板不断缩短，以保证激波刚好交汇于唇口。

对设计变量δ2在表1的状态点以攻角和马赫数为变量进行二元四次曲线拟合，得到如下的变化规律(攻角单位:(°))，图7为δ2随马赫数和攻角的拟合曲面和基于优化结果的插值曲线对比图，其中较大曲面为拟合曲面。由图7可看出，2个曲线大部分都重合在一起，说明拟合结果精度较高。

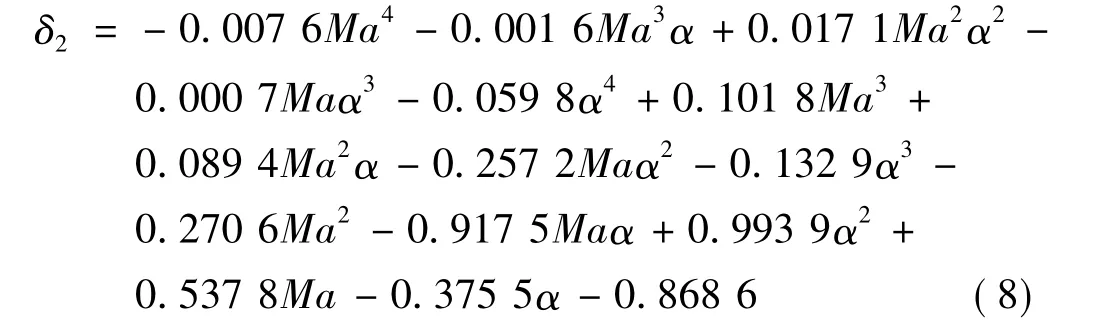
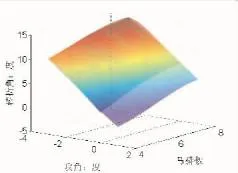
图7 δ2拟合曲面和基于优化结果的插值曲面对比Fig.7 Fiting surface verse the interpolation surface

根据式(8)求解出转折角δ2后，其余转折角、唇板长度和进气道高度分别由式(1)～式(6)计算。至此，得到不同马赫数和攻角下进气道结构变形规律，按此规律调节各楔形面转折角、唇板外缘角和长度，以及进气道高度，即可保证发动机在大飞行马赫数和攻角范围内一直高性能可靠的工作。

4 结论

(1)本文的变结构进气道设计方案，使得进气道出口高度Hinlet可变，保证了发动机在亚燃和超燃模态均能正常起动和稳定工作。

(2)在基准进气道设计时发现，在低马赫数下设计得到的进气道，工作在高马赫数时，性能下降很严重，进行结构变形后，其性能提升不大;高马赫数下设计的进气道，工作在低马赫数时，性能下降不大，进行变结构设计后，发动机性能提高。因此，选取高马赫数(一般取巡航马赫数)作为设计马赫数进行发动机进气道设计和结构变形设计，能使发动机以高性能工作。

［1］Ryan P Starkey.Scramjet optimization for maximum off-design performance［C］//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference ＆ Exhibit.Fort Lauderdale，Florida，11-14 July 2004.

［2］Ryan P Starkey.Off-design performance characterization of a variable geometry scramjet［C］//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference＆ Exhibit.Tucson，Arizona，10-13 July 2005.

［3］Marc Bouchez，Vadim Levine，Valery Avrashkov.Airbreathing space launcher interest of a fully variable geometry propulsion system and corresponding French-Russian partnership［C］//36th AIAA/ASME/SAE/ASEE Joint Pr4pulsion Conference and Exhibit.Huntsville，Alabama，17-19 July 2000.

［4］Andrew D Clark，Maj Dean Mirmirani.An aero-propulsion integrated elastic model of a generic airbreathing hypersonic vehicle［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Keystone，Colorado，21-24 August 2006.

［5］Smart M K.Optimization of two-dimensional scramjet inlets［J］.Journal of Aircraft，1999，36(2):430-433.

［6］罗世彬，罗文彩.超燃冲压发动机二维进气道多级多目标优化设计方法［J］.国防科技大学学报，2004，26(3).

［7］Matthew Brown，Neil R Mudford，Andrew J Neely.Robust design optimization of two-dimensional scramjet inlets［C］//AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference.2006.

［8］Shahriar Keshmiri，Richard Colgran，Saeed Farokhi.Airbreathing combined cycle engine for a generic hypersonic vehicle［C］//43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference ＆ Exhibit.Cinicinnati，OH，8-11 July 2007.

［9］车竞.高超声速飞行器乘波布局优化设计研究［D］.西安:西北工业大学，2006，12.

［10］Amrit Pratap，Sameer Agarwal，Meyarivan T.A fast and elitist multi-objective genetic algorithm:NSGA-II［C］//IEEE Transactions on Evolutionary Computation.2002，6(2). (编辑:崔贤彬)