掠海飞行器主动触水撞水力分析①

樊 征，刘莹莹

(西北工业大学航天学院，西安 710072)

0 引言

飞行器在入水过程中，由于其速度矢量在运动铅垂面内具有速度分量，所以此时会产生与水面的碰撞［1－3］，把这种碰撞而产生的作用力称撞水力。在研究撞水的受力过程时，通常将击水物体等效为一个近似外形和体积的刚性钝形体，并假设该物体仅沿一静止半空间流场的法向运动，流体介质为理想的不可压流，且流动有势。但在实际分析过程中，仍存在一定的难点，主要包括流动区域不能预先确定;流场边界分成了流固接触面和自由表面两部分，它们都是未知的，且自由表面的波动一般不是小幅度;待求变量与时间相关。

由于撞水过程的复杂性及上述难点的存在，目前对撞水力计算都是基于一定简化假设条件进行的。归纳起来撞水力的计算方法主要有解析法、数值法［4－5］和实验法。本文考虑到解析法具有机理明确、物理意义明显等优点，在建立水上高速飞行器防浪滑板撞水力模型时采用这种方法进行撞水力的计算和分析。同时，为了进一步验证理论式所得结果的可靠性，本文通过有限元法仿真并模拟飞行器撞水的全物理过程，仿真结果表明，解析法计算结果与有限元方法的偏差不超过8%，具有较高的可信度。

1 小斜升角楔形体撞水力计算模型

Von Karman和Wagner所提出的撞水力计算模型是针对小斜升角刚性楔形体的二维垂直对称入水问题开展的，如图1所示。同时，作出如下假设:

(1)假设流体介质为不可压无旋流;

(2)将楔形体与流体介质表面沾湿处的横截面等价为在无限流场中的一移动平板;

(3)楔形体在介质自由面处的浸湿宽度为2L0。

该楔形体在介质自由表面下的附连水质量m可表示为

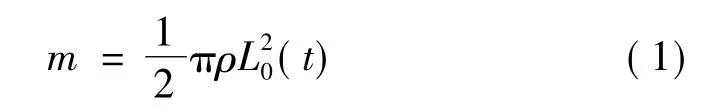
式中 ρ为流体密度。

根据动量守恒律有

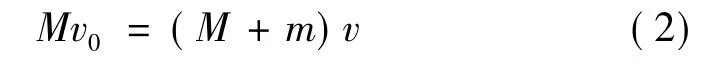
式中 M为楔形体质量;v0为入水前初始速度(方向为垂直向下);v为入水后速度。

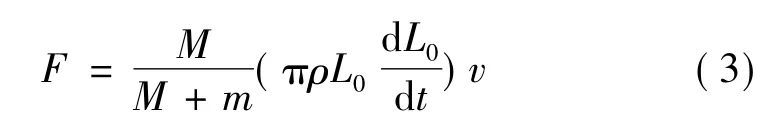
同时，由图1可知:

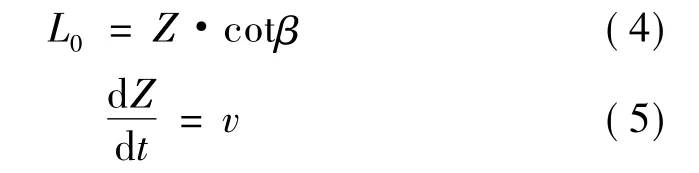
式中 Z为楔形体入水深度;β为斜升角。

则小斜升角楔形体的撞水力计算式［6－7］:

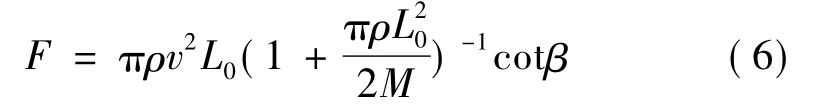
2 掠海飞行器防浪滑板撞水力计算模型

式(6)仅考虑了存在斜升角的情况，但飞行器撞水过程中存在着入水姿态问题，所以应对以上公式进行进一步变形和整理，以得到适用于飞行器实际撞水过程的力学模型。

假设条件:

(1)假设可将飞行器的击水滑板等效为一小斜升角楔形体，且板长为LB，滑板在水介质自由表面处的宽度为DB，等效后楔形体斜升角为β1;

(2)整个飞行器与滑板的总质量为M，且飞行速度在地面系Oy轴上的分量为vy;

(3)飞行器入水时存在着俯仰和滚动运动(俯仰角表示为φ，滚动角表示为γ)，且滑板与飞行器机体间属于刚性联接，无相对运动;

(4)滑板触水过程中的实际沾湿面积为S;

(5)海水密度为ρw。

据式(7)直接写出飞行器滑板在姿态运动条件下的撞水力计算模型:

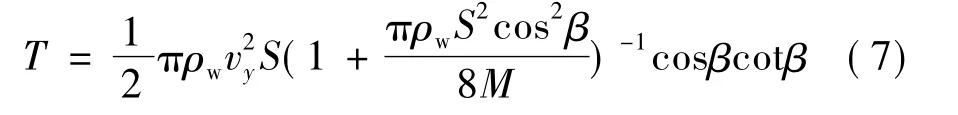
其中，β表示滑板等效为楔形体后的斜升角β1与由于飞行器姿态运动所产生的附加斜升角β2之和:

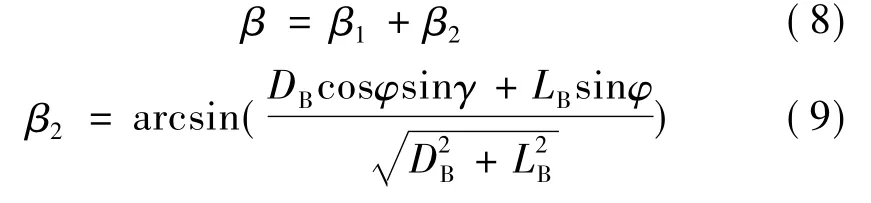
3 仿真计算

根据所得到的高速飞行器撞水力计算数学模型，可分别计算飞行器在不同入水姿态、入水弹道倾角及不同滑板斜升角情况下的撞水力。

(1)仅考虑滑板等效斜升角变化条件下撞水力的仿真计算。

当飞行器撞水时刻的绝对速度v=200 m/s，弹道倾角为 θ= －2°，滑板沾湿面积 S=1.35 m2，且每次撞水过程中姿态角不变，即φ=2°和γ=0°，通过仿真可计算飞行器撞水力与滑板等效斜升角β1之间的关系，如图2所示。

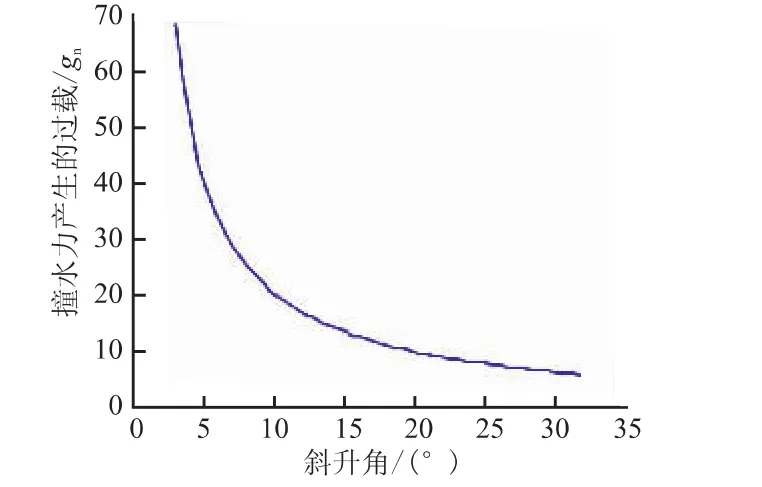
图2 撞水力产生的过载随斜升角变化曲线Fig.2 Changing curve of slamming overload under different deadrise angle conditions

由图2仿真结果可知，当飞行器入水姿态不变情况下，滑板自身的等效斜升角β1越大，则整个撞水过程中所产生的撞水力过载越小。因此，掠海高速飞行器无论是主动击水还是被动触浪，在飞行速度、入水弹道角和姿态一定情况下，要保证撞水过程中水动力对飞行器击水部件的结构强度和飞行姿态影响最小，其滑板的等效斜升角应尽量选取较大值。

(2)考虑飞行器入水弹道角、姿态角和滑板等效斜升角变化时的撞水力仿真计算。

假设飞行器撞水时刻的绝对速度v=200 m/s，滑板沾湿面积S=1.35 m2，通过式(9)可计算飞行器在不同入水弹道角、俯仰角、滚动角和滑板等效斜升角条件下的撞水力过载力。同时为了进一步验证理论式所计算结果的可靠性，文中还通过有限元方法仿真并模拟飞行器撞水的全物理过程。

LS-DYNA软件在处理流/固耦合计算方面有着诸多优势，特别适合于流固耦合流场的分析与冲击力学的计算模拟，本文选取某轴对称外形的飞行器，采用多物质ALE算法，对入水过程进行了三维有限元分析与数学仿真模拟。图3为撞水后0.2 s时刻三维仿真图，图4为飞行器质心高度坐标变化曲线。

通过对比有限元与式(9)计算所得到的仿真数据可知，在轴对称外形飞行器小倾角撞水过程中，其撞水力可采用小斜升角楔形体撞水力模型进行计算，计算结果与有限元方法的偏差不超过8%，具有较高的可信度。

由于论文篇幅限制，以下仅给出部分通过有限元方法得到的仿真计算结果，如表1和表2所示。

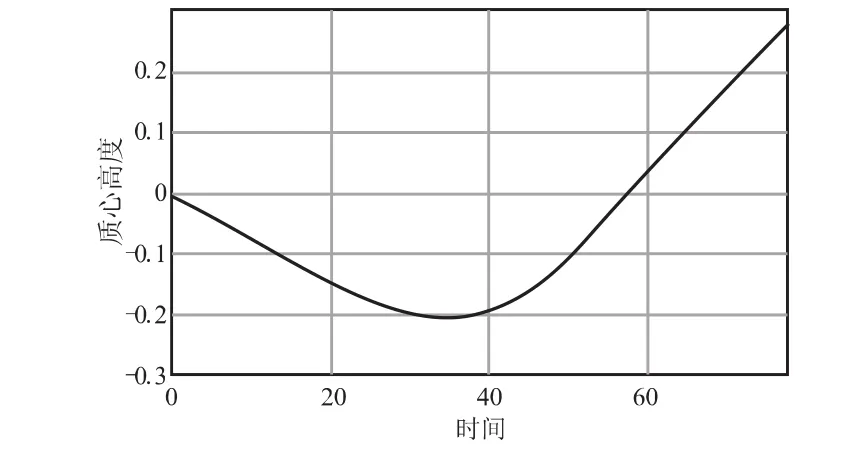
图4 飞行器质心高度坐标随时间变化曲线Fig.4 Curve of vehicle＇s centroid height coordinate

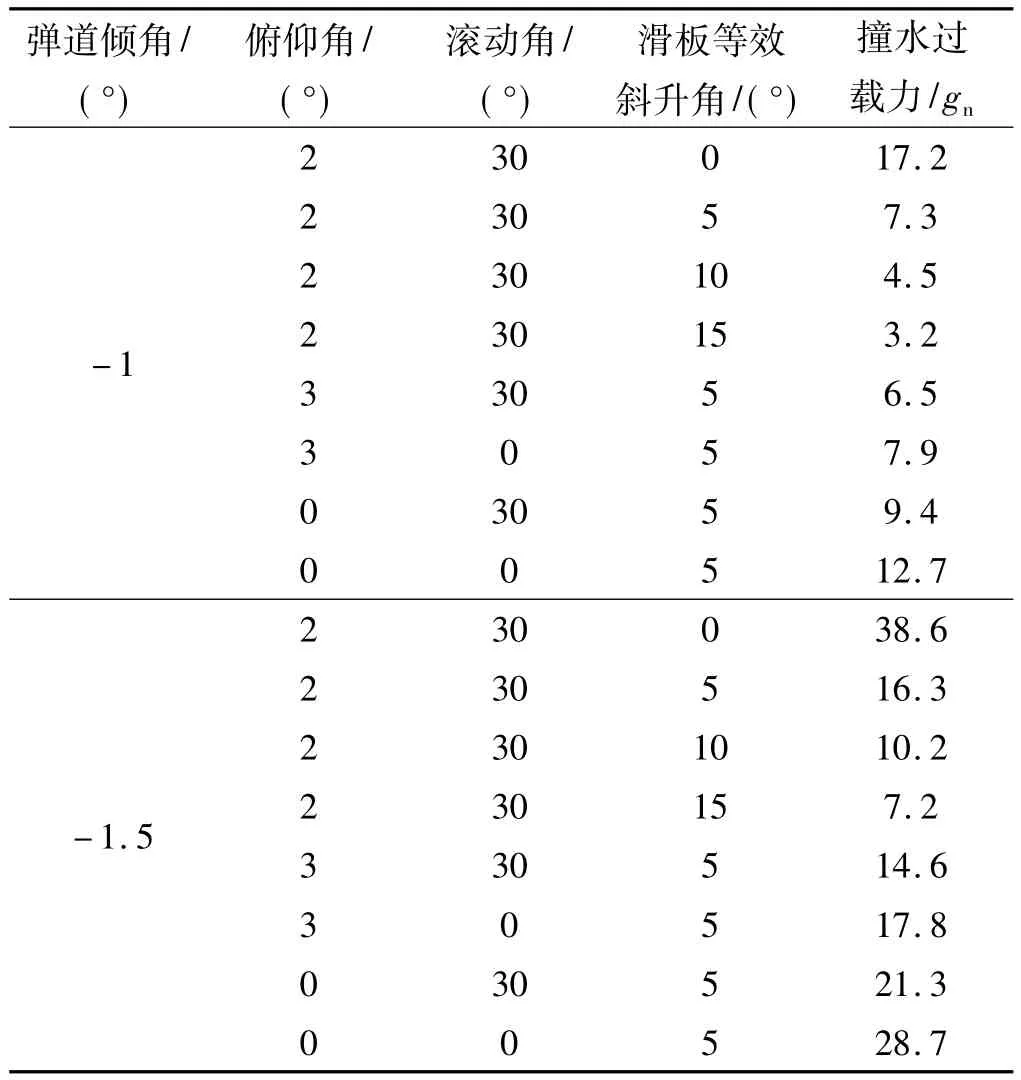
表1 入水弹道角、姿态角、滑板等效斜升角同时变化时的撞水过载力计算结果Table 1 Results of slamming overload with different water impact trajectory angle，attitude angle and slide equivalent deadrise angle

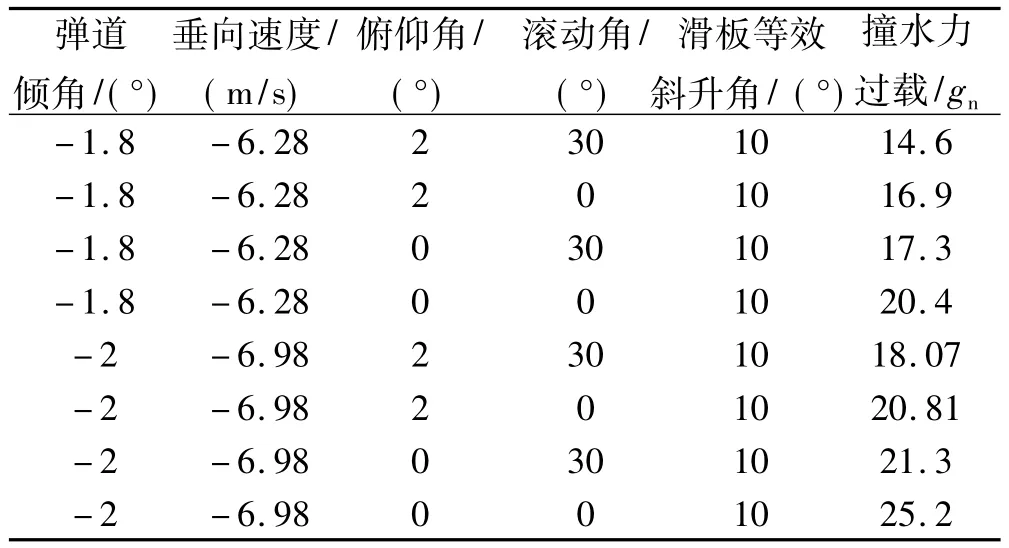
表2 入水弹道角、姿态角变化时的撞水过载力计算结果Table 1 Results of slamming overload with different water impact trajectory angle and attitude angle

4 结论

(1)飞行器入水弹道倾角的大小对撞水力的影响最大，且当入水弹道角小于10°时，其与撞水过载力之间呈线性递增的关系。

(2)除入水弹道角外，影响飞行器撞水过载力大小的因素按影响程度由大到小分别为滑板等效斜升角、飞行器俯仰角和滚动角，且变化规律为与滑板等效斜升角大小、飞行器俯仰角绝对值大小和滚动角绝对值大小呈反比关系。

(3)若水面高速飞行器撞水装置可承受的最大过载力为20 gn，则通过查表1、表2可知，飞行器入水弹道倾角应介于0°～－2°之间，同时滑板等效斜升角的大小应设计为β1≥10°，可保证入水过程中俯仰角变化范围在0°～5°、滚动角变化范围在 －30°～30°时的撞水力符合设计要求。

(4)若掠海高速飞行器撞水装置可承受的最大过载力为20 gn，且入水姿态角无限定要求，则必须满足入水弹道角在0°～－1.8°的入水条件和滑板等效斜升角β1≥10°的滑板设计条件。

(5)综合实际飞行海况、作战任务需求、控制系统的性能等方面的因素，合理选取入水弹道角、入水姿态角和滑板等效斜升角，最终在满足以上要求的前提下可实现整个入水过程的系统最优。

［1］Scott W B.Airbreathing hypersoar would bounce＇on upper atmosphere［J］.Aviation Week ＆ Space Technology，2010(7).

［2］王志东，朱仁庆.近水面航行二维水翼的水动力特性研究［J］.船舶工程，2003，26(3).

［3］Von Karman T.The impact on seaplane floats during landing［C］//National Advisory Committee for Awronautics，1990，321:145-162.

［4］王冰，叶天麒.刚体撞水非线性响应的边界元分析［J］.固体力学学报，1999，20(2).

［5］尹莉，钱勤，罗宁，等.结构撞水的流固耦合动力分析［J］.华中科技大学学报，2006，23(增刊2).

［6］Wagner H.Phenomena associated with impacts and sliding on liquid surfaces［C］//National Advisory Committee for Aeronautics，2003，1366:112-123.

［7］朱珉虎.滑行艇水动力计算［J］.中外船舶科技，2004(3).