基于EKF的无位置传感器永磁同步陀螺电机控制方法的研究

黄晓凡

(北京市普利门电子科技有限公司，北京 100041)

0 引言

永磁同步陀螺电机是航天用陀螺稳定平台中的关键部件，除了能稳定运行外，快速起动是其基本要求。无位置传感器的两相永磁同步陀螺电机克服了位置传感器安装困难、可靠性不高等缺点，逐渐得到应用。目前其控制方法主要以利用反电势过零换相控制为主，其他如基于状态观测器方法和扩展卡尔曼滤波方法(EKF)等还处于研究阶段。实时计算量大是EKF的主要缺点，运算能力强大的DSP可以有效解决这一问题。对陀螺电机而言，起动快速性是衡量控制系统性能的一个重要方面［1］，而起动快速性的前提是转子位置信号的快速获得。如果EKF能快速收敛，也就是说，迅速给出正确的转子位置信号，就给电机的快速起动提供了基本条件。

本文以ADI公司的电机专用DSP控制芯片ADMC300为主控芯片［2］，详细论述如何将 EKF应用于无位置传感器的两相永磁同步陀螺电机起动及稳态运行控制中，并论述了相应的软硬件设计。试验结果表明，在不带位置传感器的情况下，利用EKF法能有效实现永磁同步陀螺电机的自起动，而且EKF法在起动的快速性及获转子取位置信号的完整性方面比利用反电势过零换相法［3］更优越。

1 无位置传感器两相永磁同步陀螺电机数学模型

1.1 两相永磁同步陀螺电机静止α-β轴数学模型

对两相永磁同步陀螺电机而言，其两相定子绕组(a相和b相)在空间正交，构成静止α-β坐标系，其中a相轴线与α轴重合，b相轴线与β轴重合。转子上装有表贴式的磁钢。对永磁陀螺电机而言，属于空载运行，因此负载转矩为0。

电机状态空间方程为

两相定子绕组反电势分别为

式中:uα、uβ、iα、iβ、eα、eβ——分别为 α-β 轴上的两相定子电压、电流、反电势;

ψm——转子磁琏;

R——两相定子绕组电阻(两相定子绕组电阻相等);

L——两相定子绕组电感(两相定子绕组电感相等);

ωr——转子电角速度;

θr——转子电角度;

Pn——电机极对数;

J——电机转子转动惯量;

B——阻尼系数;

p——微分算子，p=d/dt。

本文中转子位置信号即是指转子电角度信号θr。

1.2 基于EKF的离散化两相永磁同步陀螺电机数学模型

在陀螺电机中，由于机械时间常数远大于电气时间常数，可以认为一个EKF采样滤波周期内ωr不变［4］，即 pωr=0(注意:不是指整个调速范围内ωr不变)。

选取X= ［eα，eβ，ωr］T为状态变量，根据式(1)、式(2)，并应用一个采样滤波周期内ωr不变的条件，建立电机的系统方程及测量方程。

系统方程为

测量方程为

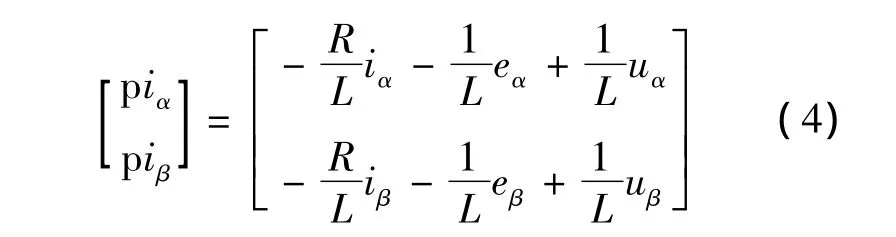
对式(3)进行离散化后得

对式(4)进行离散化后得

式(5)和式(6)称为离散化系统方程，ωk为系统噪声。式(7)和式(8)称为离散化测量方程，两相定子电压、电流(uα、uβ、iα、iβ)为测量量，vk为测量噪声。Ts为离散采样滤波周期，ωk、vk为互不相关的零均值白噪声。

2 EKF算法

EKF滤波递推公式计算步骤如下:

式中:Pk/k－1——一步预测均方误差阵;

Pk/k——估计均方误差阵;

Kk——滤波增益阵;

Q——系统噪声方差阵，要求为非负定阵;

R——测量噪声方差阵，要求为正定阵。

另外:

根据卡尔曼滤波稳定性理论，随着滤波时间的增长，状态变量估计值和状态变量估计均方误差阵Pk/k各自受其初值的影响不大，而Q，R的选取则通过试验凭经验试凑得到。另外，EKF是用线性化模型来近似原来的非线性模型，其近似程度可衡量如下:当滤波器已投入工作时，Pk/k的迹tr［Pk/k］是可以获得的，它反映了状态变量估计误差值‖Xk/k－‖的大小，可作为滤波近似程度的一种量度。

基于此，本文P0、X0、Q及R取值如下，而EKF的采样滤波周期经调试定为Ts=200 μs。

3 控制系统硬件设计

控制系统硬件部分见图1。主要由两相永磁同步电机、两相桥式功率逆变电路、电压电流传感器和基于DSP的高性能电机控制芯片ADMC300组成。其中ADMC300是核心，负责电压电流数字采样，EKF，Park逆变换等控制程序的执行。

图1 控制系统硬件图

ADMC300的PWM单元产生四路PWM信号输出(AH/AL、BH/BL)，分别与相应的两相桥式功率逆变电路的 PWM输入端相连，为其提供PWM信号。两相桥式功率逆变电路则在PWM信号作用下为电机两相定子提供所需的电压。电压、电流传感器的副边输出则与ADMC300的模数转换单元(ADC)的输入端相连，为ADC单元提供电机两相定子电压、电流的采样值。

4 控制系统软件设计

采用id=0的矢量控制方案［6］。其工作原理如下:通过电机两相电压、电流的检测，利用EKF程序得到电机转子位置信号θr，经Park逆变换程序把指令电流转化为两相绕组指令电流，，分别与采样的电流值i，i比较，通过电流调

αβ节程序，控制输入到两相桥式功率逆变电路的PWM信号占空比，使实际电流跟踪指令电流。

利用ADMC300汇编语言编制EKF，Park逆变换，电流调节，电压、电流采样等程序，构成系统的软件部分，程序流程图见图2。对各部分分别简介如下。

图2 控制系统软件流程图

(1)初始化。完成ADC单元校正，开ADC单元及PWM单元中断，设置PWM单元参数等。

(2)主循环。主循环是一个无限循环体，在每一个循环中，依次执行以下程序:EKF;Park逆变;电流调节。

(3)Park逆变换。

在id=0矢量控制方案下，Park逆变换式简化为

5 试验结果与分析

试验用永磁陀螺电机为两相定子，五对转子磁极(采用表面贴装式)，其参数如下:两相电感Lα=Lβ=L=45 μH，两相电阻Rα=Rβ=R=5 Ω，转子磁链 ψm=0.003 V·S/rad。

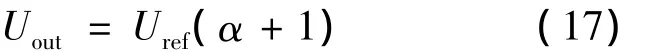
式中:Uref——ADMC300提供的2.5 V参考电压;

α——数字输入量，为定点格式;

Uout——模拟输出量。

5.1 电机起动过程中EKF收敛性验证

图3是电机从静止开始起动过程中EKF给出的转子电角度信号估计值(D/A转换后的模拟量，下同)，图 4 是Pk/k的迹tr［Pk/k］随时间变化图。可以看出经过约350 ms，tr［Pk/k］从初值 0.9(对应图2中约4.5 V)稳定在一个小值0.005(对应图中约2.5 V)。这说明EKF开始收敛，给出EKF意义上的最优估计值。

图3 电机起动过程中EKF给出的波形图

5.2 电机稳定运行过程中EKF估计转子位置信号正确性的验证

(1)反电势估计值与转子电角度信号估计值波形。

图4 电机起动过程中tr［Pk/k］波形图

图5和图6给出了通过调节指令电流，使电机分别稳定在910 r/min及4 620 r/min下的反电势估计值与转子电角度信号估计值波形图。

图 5 910 r/min 下 EKF 给出的及波形图

图 6 4 620 r/min 下 EKF 给出的及波形图

由图5、图6可以看出三者相位对应关系正确(A相反电势eα应超前B相反电势eβ90°电角度)，并且转速越低，估计出的离散位置信号越密集，宏观意义上看越接近于获得连续位置信号。反电势过零换相法只能在一个电周期内估计出4个反电势过零时的转子位置信号。

(2)EKF估计转子电角度信号正确性的验证。

下面分析如何从A相电压uα波形中提取出A相反电势eα波形。在PWM调压下，由于电机电感较小(45 μH)，电流会出现断续情况，检测到的电机A相电压信号主要由两部分组成:对应A相绕组晶体管导通、A相绕组电流不为零时加在逆变桥上的直流电压，以及对应A相绕组晶体管截止(包括序流过程)后、A相绕组电流为零时的反电势。利用PWM信号关断期间、A相绕组电流为零时的反电势，即可得到大量离散的电机A相实际反电势信号eα。图7给出了A相电压信号uα波形构成图，其小圆圈中所示均为反电势信号eα，当示波器的Display Style档打在Dots模式下可以更清楚地看出eα波形。

图7 A相电压信号uα波形构成图

图8和图9给出了2 860 r/min下的电机A相实测电压uα及A相反电势估计值波形对比图。图9中CH2(uα)波形中间的接近正弦波的那条虚线即是电机A相实际反电势eα。可见eα与A相反电势估计值吻合。由图5和图6知道B相实际反电势eβ与B相反电势估计值也必然吻合，由此可知EKF估计的转子电角度信号是正确的。

5.3 电机的起动性能对比试验

图8 2 860 r/min下的电机A相电压uα与A相反电势估计值波形对比图

图9 2 860 r/min下的电机A相电压uα与A相反电势估计值波形对比图(示波器的Display Style档打在Dots模式下)

图10 反电势过零换相法电机起动性能

利用反作用力矩测试仪［1］，图10和图11给出了同样起动电流下(0.6 A)，到达同样转速(5 000 r/min)下，分别利用反电势过零换相法和EKF法的电机起动性能对比试验。根据反作用力矩测试仪原理可知，当电机处于稳定转速时，反作用力矩测试仪测试转矩读数为零。由图10可知反电势过零换相法起动用了tqf=9 s，其中变频起动加速时间为6 s，获得可靠反电势信号后闭环控制加速时间为3 s。由图11可知EKF法起动只用了tqe=3 s。

图11 EKF法电机起动性能

6 结语

试验结果表明，在不带位置传感器的情况下，利用EKF法能有效实现永磁同步陀螺电机的自起动，而且EKF法在起动的快速性及获取转子位置信号的完整性方面比利用反电势过零换相法更优越。

［1］陆元九.惯性器件(上］［M］.北京:宇航出版社，1990.

［2］吴敏渊，金伟正，胡志雄，等.ADSP系列数字信号处理器原理［M］.北京:电子工业出版社，2002.

［3］沈建新，吕晓春，杜军红，等.无传感器无刷直流电机三段式起动技术的深入分析［J］.微特电机，1998(5):8-11.

［4］王东旭，王莉，李大喜，等.基于EKF的感应电动机无速度传感器调速系统改进研究［J］.微特电机，2009(8):33-35.

［5］秦永元，张洪钺，汪淑华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998.

［6］景军锋，康雪娟.基于DSP的永磁同步电机全数字变频调速控制系统的设计［J］.电机与控制应用，2010，37(2):43-46.