基于有限元的微型机器人足部仿真分析
蔡立斌
CAI Li-bin
(九江学院 信息技术中心,九江 332005)
0 引言
机器人是一种具有与人或生物类似的智能能力的自动化机器,兼具高度的灵活性。随着现代科学技术飞速发展,微型机器人技术作为一种多学科交叉的高科技前沿技术也取得了长足发展,并在工业生产、日常生活活动中得到广泛应用,如微型制造,医药以及血管的修复、治疗等方面,其控制精度可以达到几微米左右[1]。
有限元技术是由应用数值分析技术迅速发展而来的一项数值计算技术,在大多数工程应用及设计研究领域得到了广泛的应用,它是一种结合数值分析技术与计算机技术交叉高度综合的科学技术[2]。目前,我国的微型机器人设计与研究已向产业化方向发展,如果要实现中国机器人研发的产业化,就必须在从机器人关键零部件单元、机器人本体的优化设计以及总体性能设计等方面入手,开展相关的研发工作。而数值仿真技术的飞速发展,不仅缩短了机器人的研发周期,降低了研发成本,而且推动了机器人技术向高精尖的精密控制领域的发展[3]。
1 材料及仿真模型的建立
本微型机器人足部行走的方式与传统机器人的足部有很大差异,它是足部导通电流产生热引起足部变形而行走的。
本文根据微型机器人足部的工作原理,建立了硅质微机器人足部三维模型。图1表示的是硅质微型机器人足部的纵向截面示意图。微型机器人采用基于聚酰亚胺V型槽关节使微型机器人各条腿协调配合,从而进行自由运动的。用于制造V型槽关节的聚酰亚胺材料具有较高的热膨胀系数,因此当V型槽关节通电流运动时,聚酰胺受热,因此腿部会发生轻微弯曲。通过在微型机器人每条腿设置几个V型槽,就可以获得足够的偏转和弯曲挠度,从而实现机器人的运动(如图1所示)。该微型机器人足部仿真分析所用到的材料:制备加热电阻的聚甲基苯基硅氧烷,机器人足部的硅和氮化硅,制备复合层的氧化硅和铝,固化聚酰胺。
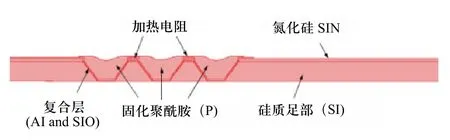
图1 硅质微型机器人足部的纵向截面示意图
该有限元模型是一个瞬态传热电分析与准稳态热机械分析相结合的模型,因此该有限元分析是一个电-热-结构耦合分析,采用COMSOL Multiphysics的电流模块、传热模块和结构力学模块来构建该微型机器人足部有限元分析模型。
为便于准确计算和分析,该模型进行了如下处理和假设:
1) 为便于模型建立,将热传导边界条件等效为对流边界条件。建模时的初始二维模型由超薄层构成的,为了减少在三维模型的网数量,对这些薄层进行必要的删除操作是很有必要的。
2) 传热模型采用瞬态热传导对流进行求解,结构模型则采用准稳态固体力学进行求解,为解决电-热-结构的问题,在力学模型中采用批处理策略和参数扫描法,将时间t设为扫描参数,这样既解决了求解的稳定性问题,又解决了热结构耦合的难题。
3) 很多数值模型都是采用单向热电耦合——电流影响产热,这种方法虽然增加了求解的收敛性,但无法反映温度等对电阻产生的影响。因此,本文热电模型采用热电双向耦合处理。
此模型涉及电-热-结构多场耦合的问题,因此该分析包括三部分:1)涉及微机器人足部电流模型分析;2)涉及电流产热及机器人热传导-对流传热模型分析;3)涉及微机器人足部受热变形的结构模型分析。
1.1 电流模型
微型机器人启动后,电流流过加热电阻时,根据欧姆定律会产生一定量的电阻热,这部分热量就作为该模型的热源。其电流PDE控制方程为,

其中s为电导率,V为电势,Je为为外部电流密度,Q为电流源。
其中电导率s是电阻率R的倒数:

其中R0为参考电阻率,T0为参考温度。
1.2 传热模型
此微型机器人模型中,采用基于固体传热的三维瞬态传热控制方程。其控制方程包括热传导和对流项:

其中k,r,C是材料的热传导系数、密度和比热,它们都是温度的函数;Q和v分别是热源强度(即电流模型中电流的总功率损耗密度)和运动速度。
传热模型的另一个重要部分是在机器人模型对流冷却边界的建模。实验证实,机器人通过加热电阻产生的大部分热量是从硅结构表明也就是在机器人的“身体”与周围环境发生对流而释放热量的。此外,足尖端与地面之间是热传导边界,为了简化建模,将热传导边界条件等效为对流边界条件,其对流冷却控制方程描述如下,

其中Text是周围环境的温度。采用较高的热传导性边界作为铝复合层传热边界。用刚性弹簧条件来描述电阻层,其控制方程如下,
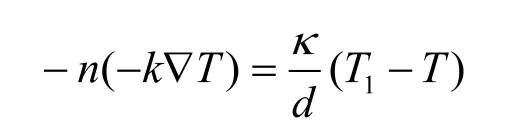
其中d为复合层厚度。此模型除与地面接触的足尖端部分采用对流系数为1×104W/(m2·K)外,该机器人模型其余部位采用对流系数为1×105W/(m2·K)。在这里,对流系数的取值是随意选择的,但可以通过比较模拟结果与实验数据来重新校正热传导系数。
1.3 力学模型
此微型机器人力学模型是基于COMSOL中的固体力学模型和线弹性材料模型建立的。其力学模型的控制方程为:
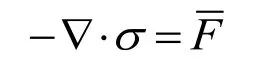
力学部分的边界条件:约束机器人足底部左侧的位移,而机器人结构的其余部分受力为零。三维模型中不包括Al和 SiO复合薄层。对由此产生的边界,通过一个结构壳和两个特定的热边界条件来模拟高热传导层和低热传导层。热量传输通过机器人足部传导时,由于几种材料的热膨胀系数的不同而导致足部出现弯曲行为。在刚性弹簧边界条件下模拟的边界温度是间断的,因此需要建立两个传热模型。结构分析部分采用一个热膨胀壳单元来模拟两个薄层。COMSOL软件会自动处理热膨胀外壳和固体单元之间的耦合。
2 结果与讨论
本模拟中,在两个电阻上都施加30mV的电势持续时间0.1ms,通过电流模型中电流的总功率损耗密度计算可知,由电阻热产生的热量源约为2·1013W/m3,相当于100 mW的热量输入。
结构力学部分的时间尺度与传热部分相比要小得多,所以可忽略结构分析中的质量效应。使用参数扫描分析将瞬态结构分析转换为准稳态结构分析。这种方法把固体分析和传热分析结合起来,通过顺序求解方式来进行模型的求解:首先求解传热和导电介质DC偏微分方程,然后,将计算结果存储在指定文件中,设置指向存储的计算机结构的线性化路径,用时间变量参数t作为扫描参数来求解结构力学偏微分方程。图4 所示在t=0.1ms和t =0.2ms时微型机器人足部的温度场分布,从图中可以看出t=0.1ms时,机器人足部最高温度出现在加热电阻处,t=0.2ms时,由于聚酰胺良好的导热性,热量传递到V型槽,因此这时最高温度出现在V型槽。

图2 在t=0.1ms和t=0.2ms时微型机器人足部的温度场分布
图3所示分别在t=0.1ms和t=0.2ms时微型机器人足部的变形(图中黑色框图表示未变形前的位姿,彩色框图表示变形后的位姿),从图3中可以明显看出微型机器人的发生弯曲变形等现象,同时,正如预期的那样足部的弯曲位移随着温度的增加而增大,当关闭电源(热源)时机器人足部弯曲复原。图4所示为微型机器人足部总位移随时间的变化曲线,位移变化曲线的仿真和实验结果的变化规律一致,在0.1ms弯曲挠度达到最大,在0.1ms后由于关闭电源(热源)使其温度迅速降低,导致机器人足部弯曲挠度也变小。
3 结论
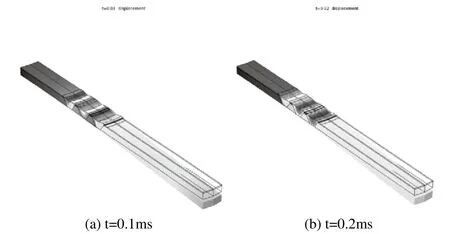
图3 在t=0.1ms和t=0.2ms时微型机器人足部的变形
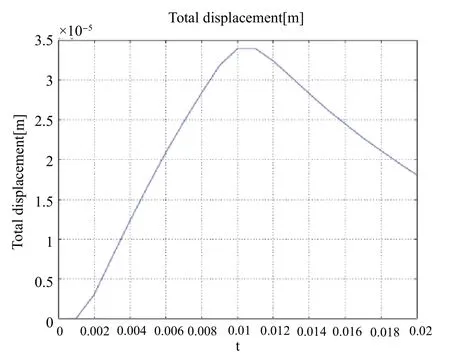
图4 足尖的总位移 (随时间变化)
本文在分析了微型机器人足部工作原理的基础上,基于多物理场耦合原理,利用COMSOL多物理场耦合分析软件建立了微型机器人足部三维电-热-结构耦合模型,模拟并分析了硅质微型机器人运动过程中足部的温度场以及弯曲变形行为。微型机器人足部弯曲变形等行为的模拟仿真结果与实验结果取得了很好的一致性,因此该有限元模型是可以准确预测微型机器人足部的弯曲变形等行为。
[1]柴婷婷, 丁言露. 机器人仿真及其自动化研究进展[J]. 制造业自动化, 2011, 33(5): 87-89.
[2]俞志伟, 杨屹巍, 宫俊, 戴振东. 基于LPC2103的仿壁虎机器人控制系统设计[J]. 制造业自动化, 2011, 33(11):6-10.
[3]肖智勇, 段建中, 杜鑫强, 李建. Motoma工业机器人有限元静态分析及改进设计[J]. 长沙理工大学学报, 2011,8(4): 71-76.

