基于混凝土损伤塑性模型的桥墩地震响应分析
王 维,何丽丽,李涛涛,黄 信
(1.天津市水利勘测设计院,天津 300072;2.天津市建筑设计院结构研发中心,天津 300072)
基于混凝土损伤塑性模型的桥墩地震响应分析
王 维1,何丽丽1,李涛涛1,黄 信2
(1.天津市水利勘测设计院,天津 300072;2.天津市建筑设计院结构研发中心,天津 300072)
为确保桥梁结构在强震作用下的安全,对钢筋混凝土桥墩进行了地震响应分析。基于损伤因子建立混凝土损伤塑性模型,考虑混凝土材料在动力荷载作用下的损伤演化,并利用损伤塑性模型对钢筋混凝土桥墩进行地震响应分析,同时分析了损伤塑性模型中膨胀角等参数对桥墩地震响应的影响。分析表明:混凝土损伤塑性模型能够较好地模拟混凝土构件在动力荷载作用下的损伤发展,所以在钢筋混凝土桥墩动力分析中应采用损伤塑性模型描述混凝土材料力学性能。
钢筋混凝土桥墩;地震响应分析;损伤塑性模型;损伤因子
1 研究背景
桥梁结构作为交通运输枢纽发挥着重要作用,然而在强震作用下桥梁结构会发生严重损坏,从而使交通运输中断并造成巨大的经济损失。许多学者对桥梁抗震进行了深入的研究[1-2],主要包括地震动输入、地震反应分析方法、土-结构相互作用及结构非线性问题等方面。桥梁结构在地震作用下上部结构破坏比较少见,桥墩震害往往是引起桥梁倒塌并在震后难以修复使用的主要原因[3],所以为确保桥梁结构的安全,应对桥墩结构在地震作用下的动力响应进行分析。
现有桥墩主要采用钢筋混凝土材料,选择合适的混凝土本构模型对于在数值分析中获得正确的桥墩地震响应至关重要。混凝土本构主要分为弹性本构和塑性本构,弹性本构仅适用于混凝土受载初始阶段,当材料出现非线性行为后应采用塑性本构,损伤是导致应力应变关系非线性和不可逆变形的主要原因[4]。混凝土材料的性能在很大程度上取决于其内部微裂缝,在荷载作用下混凝土内部的微裂缝会扩展和汇合,最后形成宏观裂缝并导致强度、刚度等性能的劣化甚至材料破坏即材料发生损伤,许多研究者基于连续介质力学和不可逆热力学,在本构模型中引入损伤变量表征微观缺陷对材料宏观力学性质的影响,构造带有损伤变量的本构模型描述混凝土材料的性能[5-12]。Lee J等建立损伤塑性连续本构并对混凝土坝进行地震响应分析,该本构能够很好地描述混凝土材料的应变软化、刚度退化及恢复等特性[6]。Peter G基于有效应力和塑性应变建立了考虑混凝土失效的三轴损伤塑性本构,并应用于钢筋混凝土柱的分析[7]。Ludovic J等基于各向同性损伤和受压屈服塑性面建立了损伤弹塑性本构,并利用试验对本构模型进行了验证[8]。张劲等基于ABAQUS软件对Lee J等建立的混凝土损伤塑性模型参数的确定进行了研究[10]。方秦等也利用ABAQUS软件验证了Lee J等建立的损伤塑性模型在分析混凝土材料和构件静力性能的有效性[11]。然而对于结构动力分析中混凝土材料采用弹性本构和塑性损伤本构对结构响应的差异尚无具体研究,同时损伤塑性模型中膨胀角等参数在数值分析中一般按默认值取值,所以本构模型中相关参数取值对结构动力响应计算结果的影响也尚待研究。
本文基于ABAQUS软件并利用Lee J等建立的损伤塑性模型描述混凝土的力学性能,对钢筋混凝土桥墩进行地震响应分析,同时进一步探讨了该混凝土损伤塑性模型中相关参数对桥墩动力响应的影响。
2 混凝土损伤塑性模型
Lee J等建立的损伤塑性模型可以用于混凝土材料在动力荷载作用下的分析,认为在低静水压力作用下,混凝土材料的损伤主要是由于受拉开裂和受压破碎导致的。该本构模型可以描述在受拉和受压下的刚度退化、滞回荷载作用下的刚度恢复以及应变率的影响[6,12]。
2.1 应力-应变关系
通过修正初始弹性刚度考虑材料受力后发生的损伤,建立应力-应变关系为

式中:Del0为初始弹性刚度;Del为损伤后的弹性刚度;d为损伤变量;ε为应变;εpl为塑性应变。有效应力定义为

2.2 损伤因子
混凝土材料在单轴受拉或受压作用下由于开裂或压碎产生损伤从而导致刚度下降,如图1所示。此时通过引入损伤因子考虑刚度下降,损伤因子表达式如式(3)所示:

式中:t,c分别代表拉伸和压缩;β为塑性应变与非弹性应变的比例系数,受压时取0.35~0.7,受拉时取0.5~0.95;εin为混凝土拉压情况下的非弹性阶段应变;σk为应力;E0为初始弹性模量。

图1 单轴滞回荷载作用下应力-应变关系Fig.1 Stress-strain curve under uniaxial hysteretic load action
在往复荷载作用下,混凝土材料由拉到压,由于裂缝的闭合会发生刚度恢复现象,为此引入参数st和sc,此时损伤变量表示为

式中参数st和sc为应力的函数,具体公式如下:

其中,当¯σ11>0时为受拉状态,此时r*(¯σ11)=1,当¯σ11<0时为受压状态,此时r*(¯σ11)=0;ωt,ωc为权重系数。试验得到混凝土由拉到压的过程中由于裂纹的闭合存在压缩刚度恢复现象,而由压到拉则不存在拉伸刚度恢复,所以ωt=0,ωc=1。
2.3 屈服条件及流动法则
通过有效应力定义屈服函数为

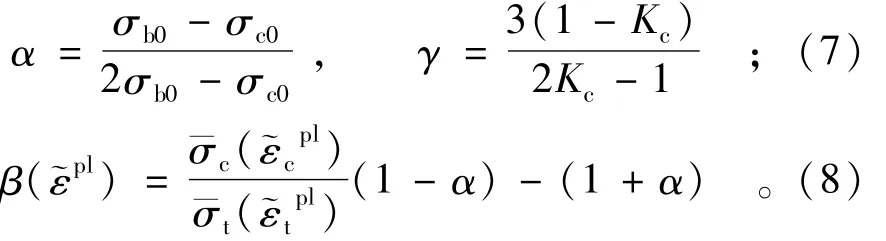
损伤塑性模型采用非相关势流法则,表达式如式(9)所示:

其中流动势G采用Drucker-Prager双曲线函数
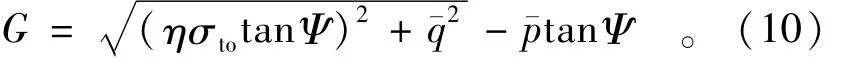
式中:σto为单轴拉伸失效应力;η为偏心率;Ψ为膨胀角,取值一般由试验确定。

图2 钢筋混凝土桥墩模型Fig.2 RC bridge pier model
3 数值分析模型的建立
3.1 分析模型
桥墩为实心矩形截面,截面尺寸为4 m×5 m,墩高为40 m;采用附加质量考虑桥梁上部结构对桥墩墩顶的约束作用,墩顶集中质量取一跨梁桥面系的质量为5.6×105kg;阻尼采用瑞雷阻尼。混凝土桥墩模型采用实体单元C3D8R,该单元为三维实体单元包含减缩积分,可以较好地模拟混凝土性能;钢筋采用T3D2单元模拟,该单位桁架单元可以模拟钢筋特性。图2所示为钢筋混凝土桥墩模型。
3.2 材料参数
混凝土弹性模量为2.65×1010Pa,密度为2 400 kg/m3,泊松比为0.17;塑性参数如表1所示,单轴荷载作用下受拉和受压的应力与应变关系如图3所示,损伤因子与非弹性应变关系见文献[12],其中拉伸恢复系数为0,压缩恢复系数为1。钢筋弹性模量为2.10×1011Pa,屈服应力为335 MPa,泊松比为0.3,纵筋直径为20mm,箍筋直径为10mm,间距为200mm。

表1 混凝土材料塑性参数Table 1 Plastic parameters of concretematerial

图3 单轴荷载作用下受拉、受压应力与应变关系Fig.3 Stress-strain curves under uniaxial load action
4 钢筋混凝土桥墩地震响应分析
4.1 损伤塑性模型对桥墩地震响应的影响
混凝土分别采用弹性本构、塑性本构和损伤塑性本构,其中塑性模型即为不考虑材料刚度退化;并利用天津波(1976年,EW方向)和El-Centro波(1940年,EW方向)的加速度时程进行地震激励,加速度峰值取0.1 g和0.2 g;分析混凝土采用不同本构模型时桥墩地震响应的差异。计算得到钢筋混凝土桥墩的墩底应力和墩顶最大相对位移幅值如表2所示,墩底应力为Mises应力。

表2 地震作用下桥墩墩底应力和墩顶相对位移幅值Table 2 M agnitude of stress on the bridge pier bottom and relative displacement on the pier top under earthquake action
从表2可以得到,在El-Centro波激励下,加速度峰值无论是0.1 g还是0.2 g,混凝土分别采用弹性本构和损伤塑性本构下,桥墩结构的应力和位移响应在明显差异,如采用弹性本构时墩底应力为4.30 MPa,采用塑性本构时墩底应力为5.81 MPa,采用损伤塑性本构时墩底应力为6.05 MPa。同样对于天津波也可以得到类似结果。由于所选2条地震波频谱特性不同,所以计算结果存在差异;对于本文结构而言,天津波作用对桥墩结构的作用较大,从而使桥墩塑性发展更大。
图4分别给出了桥墩在El-Centro波作用下,混凝土采用3种不同本构时桥墩墩顶相对位移时程。
由图4可知,加速度幅值为0.1 g时混凝土采用3种本构计算的桥墩位移时程差别较小,而当加速度幅值0.2 g时采用3种本构计算所得的桥墩位移时程差别较为明显;这是因为在峰值0.2 g的强震作用下桥墩混凝土材料进入非线性,此时如果仍按弹性本构进行分析则会得到不合理的结构动力响应结果,所以结构进入非线性时应采用塑性本构描述材料的力学性能;同时从图4(b)中还可以看出塑性本构和损伤塑性本构下的桥墩位移时程也存在一定的差别,这主要是相对塑性本构而言,损伤塑性本构可以考虑混凝土材料在受力过程中的刚度退化以及往复荷载作用下的刚度恢复的特性。

图4 El-Centro波作用下桥墩墩顶相对位移时程Fig.4 Time-history curves of relative displacement on the bridge pier top under El-Centro wave excitation
图5 分别给出了El-Centro波作用下桥墩拉伸破坏变量(DAMAGET)和刚度退化变量(SDEG),其中拉伸破坏变量代表了桥墩的破坏情况,而刚度退化变量代表了混凝土的开裂情况,地震波加速度峰值为0.2 g。

图5 El-Centro波作用下桥墩拉伸破坏变量和刚度退化变量Fig.5 Variables of tension failure and stiffness degradation of bridge pier under El-Centro wave excitation
从图5(a)可以看出拉伸破坏变量的大小随着材料的拉伸破坏只增不减,而从图5(b)可以看出刚度退化变量的大小随着裂纹的开合情况却是或增或减的,它反映了混凝土结构刚度自我恢复的性质,所以损伤塑性本构可以较好地描述混凝土材料在动力荷载作用下的损伤发展。
4.2 损伤塑性模型参数对桥墩地震响应的影响
为更加详细地研究损伤塑性模型,分析损伤塑性模型中的膨胀角、Kc和σb0/σc0等参数取值对桥墩地震响应的影响;分别利用El-Centro波和天津波加速度时程进行地震激励,加速度峰值取0.2 g;分别改变本构模型中相应参数取值以分析其对桥墩地震响应的影响。表3给出了本构模型参数取不同值时计算得到的桥梁结构动力响应。
从表3可以得到,在El-Centro波作用下,损伤塑性本构中的膨胀角变化会对桥墩的动力响应产生一定的差异,而σb0/σc0和Kc数的变化对桥墩结构动力响应的影响并不明显,如参数默认取值情况下桥墩墩底应力为8.22 MPa,而当膨胀角为30°时桥墩墩底应力为8.08 MPa,应力比为1.1时桥墩墩底应力为8.21 MPa,Kc=0.9时桥墩墩底应力为8.22 MPa。同样对于天津波作用也可以得到类似结论。

表3 考虑本构模型参数影响下的桥墩墩底应力和墩顶相对位移幅值Table 3 M agnitude of stress on the bridge pier bottom and relative displacement on the pier top considering model parameters
5 结 论
(1)强震作用下桥墩材料进入非线性阶段,此时应采用损伤塑性模型描述混凝土的力学性能对桥墩进行地震响应分析。
(2)损伤塑性模型可以获得桥墩结构破坏和开裂的发展过程,从而能够较好地描述桥墩结构在动力荷载作用的刚度退化及损伤演化过程。
(3)损伤塑性模型中膨胀角取值对桥墩结构动力计算结果有一定的影响,而σb0/σc0和Kc的取值对结构动力计算结果的影响不明显。
[1] 刘光栋,周建春.大跨度公路桥梁抗震分析的若干研究进展[J].湖南大学学报,1996,23(5):105-112.(LIU Guang-dong,ZHOU Jian-chun.Research Advances in Seismic Response Analysis of Large-span Highway Beam Bridges[J].Journal of Hunan University,1996,23(5):105-112.(in Chinese))
[2] 王克海,李 茜.桥梁抗震的研究进展[J].工程力学,2007,24(增2):75-82.(WANG Ke-hai,LIQian.Research Progress on Aseismic Design of Bridges[J].Engineering Mechanics,2007,24(Sup.2):75-82.(in Chinese))
[3] 范立础,胡世德,叶爱君.大跨度桥梁抗震设计[M].北京:人民交通出版社,2001.(FAN Li-chu,HU Shi-de,YE Ai-jun.Large-span Bridges Seismic Design[M].Beijing:China Communications Press,2001.(in Chinese))
[4] 姜锡权,方秦.混凝土本构描述的几个问题探讨[J].工程兵工程学院学报,1999,14(1):1-5.(JIANG Xiquan,FANG Qin.Discussion on Several Problems of Concrete Constitutions[J].Journal of Nanjing Engineering Institute,1999,14(1):1-5.(in Chinese))
[5] 何建涛,马怀发,陈厚群.混凝土损伤本构理论研究综述[J].水利水电科技进展,2010,30(3):89-94.(HE Jian-tao,MA Huai-fa,CHEN Hou-qun.Research Review on Concrete Damage Constitutive Theory[J].Advances in Science and Technology of Water Resources,2010,30(3):89-94.(in Chinese))[6] LEE J,FENVESG L.A Plastic-Damage Concrete Model for Earthquake Analysis of Dams[J].Earthquake Engineering and Structural Dynamics,1998,27(9):937-956.
[7] PETER G,MILAN J.Damage-Plastic Model for Concrete Failure[J].International Journal of Solids and Structures,2006,43(22/23):7166-7196.
[8] LUDOVIC J,ANTONIO H,GILLESP-C,et al.An E-lastic Plastic Damage Formulation for Concrete:Application to Elementary Tests and Comparison with an Isotropic Damage Model[J].Computer Methods in Applied Mechanics and Engineering,2006,195(52):7077-7092.
[9] ZHANG J,ZHONG ZX,CHEN CY.Yield Criterion in Plastic-Damage Models for Concrete[J].Acta Mechanica Solida Sinica,2010,23(3):220-230.
[10]张 劲,王庆杨,胡守营,等.ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构,2008,38(8):127- 130.(ZHANG Jin,WANGQing-yang,HU Shou-ying,et al.Parameters Verification of Concrete Damaged Plastic Model of ABAQUS[J].Building Structure,2008,38(8):127-130.(in Chinese))
[11]方 秦,还 毅,张亚栋等.ABAQUS混凝土损伤塑性模型的静力性能分析[J].解放军理工大学学报(自然科学版),2007,8(3):254-260.(FANG Qin,HUAN Yi,ZHANG Ya-dong,et al.Investigation into Static Properties of Damaged Plasticity Model for Concrete in ABAQUS[J].Journal of PLA University of Science and Technology,2007,8(3):254-260.(in Chinese))[12]ABAQUS,Inc.ABAQUSTheory Manual(Version 6.6)[K].USA:ABAQUS,Inc,2006.
(编辑:周晓雁)
Seism ic Response of Bridge Pier Based on Plastic-Damage M odel for Concrete
WANGWei1,HE Li-li1,LITao-tao1,HUANG Xin2
(1.Tianjin Water Conservancy Survey Design Institute,Tianjin 300072,China;2.Structure R&D Center,Tianjin Architecture Design Institute,Tianjin 300072,China)
To analyze the seismic response of reinforced concrete(RC)bridge pier,a plastic-damage model for concrete is established based on damage factors.The evolution of concrete damage under dynamic load is considered.In addition,the influence ofmodel parameters such as dilation angle on the seismic response of RC bridge pier is analyzed.It’s found that the damage evolution of RC bridge pier under earthquake action can be better simulated through plastic-damagemodel,which,therefore,could be adopted to describemechanical properties of concrete in the dynamic analysis of RC bridge pier.
RC bridge pier;seismic response analysis;plastic-damagemodel;damage factor
U442.55
A
1001-5485(2012)06-0079-04
2011-10-19
王维(1983-),女,江苏徐州人,助理工程师,硕士,从事水利水电工程规划、设计工作,(电话)13602121349(电子信箱)wangw831102@163.com。

