时延和能耗均衡的强连通支配集构造算法
孙彦景,钱建生,马姗姗,任鹏
(1. 中国矿业大学 信息与电气工程学院,江苏 徐州 221116;2. 中国矿业大学 煤炭资源与安全开采国家重点实验室,江苏 徐州 221116)
1 引言
与传统计算机网络不同,无线传感器网络(WSN, wireless sensor networks)没有固定的基础结构。依据图论的独立集、支配集、连通支配集、独立支配集、团簇及染色等基本理论[1],研究人员提出了很多构造层次网络的方法,作为无线传感器网络的虚拟骨干[2]。在单位圆图(UDG, unit disk graph)网络模型的基础上,学者对使用最小连通支配集构造虚拟骨干的方法进行了大量的研究[3],提出了很多最小连通支配集(MCDS, minimum connected dominating set)的构造算法。
文献[4~6]主要研究高效的分布式MCDS算法,或者在一定程度维护虚拟骨干的冗余以保证容错性和路由的灵活性。文献[7]针对最小连通支配集问题提出了具有较高能量效率的启发式算法。该算法把网络中所有的节点作为最小连通支配集的一个初始解,然后利用启发式修剪策略剔除冗余节点从而减小最小连通支配集的规模。文献[8]使用图着色算法求得的极大独立集等价于簇划分后的簇头集合,然后搜索网关节点使得簇头连通,由此生成极小连通支配集,形成虚拟主干网。文献[9]提出一种基于能量代价的最小权和连通支配集拓扑控制算法,解决无线传感器网络中最小连通支配集拓扑并非网络耗能最小拓扑的问题,最小化网络整体能耗。文献[10]为了提高无线传感器网络的能量利用效率、延长网络的生存时间,提出了用马尔科夫模型优化分布式最小连通支配集算法。文献[11]在串行最大独立集构造算法的基础上,提出了基于权重和时序的触发式连通支配集构造算法。
随着传感器网络应用范围的迅速扩大,不仅要考虑节能特性,同时也对传输时延提出了要求。文献[12]提出采用一种新型动态树来组织网络拓扑的能效与时延平衡的数据收集机制。文献[13]提出了一种基于虚拟点优先级的移动sink路径优化选择方法,以满足时延要求和最小化网络整体能耗。就无线传感器网络而言,在单位长度下,路径长度等相关因素决定了网络数据在节点之间的传输时延。在网络图上,路径长度转化为最短路径树(SPT,shortest path tree)问题,等效于传输时延。数据传输带来的能量功耗则可以看作求解最小支撑树(MST,minimum spanning tree)问题。文献[14]的研究结果表明不可能满足路径和费用同时最小的要求。在文献[15]的基础上,文献[16]提出了理想情况下基于无向图的有界传输时延连通支配树问题,并给出了构建CDT(connected dominating tree)的有效算法,构建连通支配树来平衡连通支配集中功耗和传输时延。
考虑到无线网络中通信链路的非对称性,本文使用加权有向连通图建模无线网络,在文献[16]的基础上提出对应无线传感器网络有界传输时延强连通支配树联合约束问题,并给出基于有向加权图的时延和能耗均衡的强连通支配集算法,验证了算法的有效性。
2 SDTT问题
在无线网络中,相邻节点间的边权重并不是对称的,例如,节点u和v在不同噪声环境下,有不同的信号检测阈值,这样从u到v和从v到u的路径上发送的功率也就不同,依图论理论,本文使用有向图进行网络建模。
文献[14]研究表明不可能同时满足最小化权重和距离的目标。为平衡MST和SPT的目标要求,本文分别以MST和SPT的费用(权重)表示发送时消耗的能量和从发送方到接收方的路径长度,构造具有双重权值的生成树。同时,为简化分析,以路径长度代替传输时延。这样,对强连通支配集的生成树而言,目的是在能量消耗(α)和传输时延(β)要求之间进行折中。设加权有向图G=(V, E),要找到支撑G满足(α,β)约束要求的强连通生成树C,相关符号沿用文献[16]中的定义:
Puv:从节点u到v发送成功所需要的功率
d(u, v) 或d(e):在单位长度下,从节点u到节点v沿边e的欧氏距离;
Cv:信号侦测阈值常量,与具体环境条件相关。无线信号传输消耗的能量正比于dγ,γ的取值是从2到4,本文设为2;
p(u):从节点u到节点v的最大发送功率为p(u)=max{puv:(u,v)∈G};
w(e):从节点u到节点v的边e的权重为
w(C):强连通树C的权重w(C) = Σe∈Tw(e);
p(C):强连通树C的能量消耗p(C) = Σu∈Vp(u);
d(G):图G的路径长度(传输时延)d(G)=Σe∈Ed(e)。
定义1 无线传感器网络有界传输时延强连通支配树约束(SDTT)问题:给定无线传感器网络子集,构建一个 SCDT-tree,使得d(SCDT)不大于用户设定的阈值,并且p(SCDT)有界。
通过构建一个强连通SCDT,同时满足能量均衡和传输时延约束的要求。据文献[16]SCDT-tree定义如下:
定义2 如果图G的强连通支配树C在α≥1且β≥1时,满足下面的要求,则称C为图G的SCDT-tree:
1) 距离:对每一个顶点u,根节点r与u之间的距离至多是从r到u的最短路径的α倍;
2) 能耗:C的能量消耗最多是SDTT问题最优解的β倍。
针对链路的不对称性,本文使用加权有向连通图建模无线网络,提出对应SDTT问题在有向加权图中的SCDT算法。
3 SCDT算法
在加权有向连通图上,该图的最小费用树把节点对间的发送功率作为权值,最短路径树以路径长度为权值,任选根节点r,SCDT算法构建能耗和时延均衡的强连通支配树。
算法构造以r为根的MSTT和以r为汇聚点的T´,通过二者的叠加得到强连通图。依据网络的连通信息构建H,H包含从根r至每个顶点的最短路径;使用文献[17]提出的MWIA-TC算法构建T和T´。
SCDT算法按深度优先(DFS, depth first search)的方式遍历最小生成树T,当访问节点u时,如果在T中从r到u的路径长度大于α倍H中的最短路径,则用H中从r到u的路径取代T中的路径。对于T´执行同样的过程。这样,在遍历所有节点后,SDTT问题得以解决。算法输入α,r, MSTT,MSTT′和SPTH,最后返回SCDT-treeC。
算法1 SCDT算法


4 分布式强连通支配集算法
分布式强连通支配集算法过程分为2个阶段,首先在单位圆图构建极大独立集,然后基于有向图使用分布式SCDT算法构造时延和能耗均衡的强连通支配集。
4.1 分布式MIS构建
采用文献[18]的方法让所有的节点知道自己的排序和邻居后,根节点启动染色标记过程构建极大独立集。使用分布式簇头选择算法构建有根生成树进行等级排序的机制,以保证生成的极大独立集满足两跳的标准。在生成的有根生成树中每个节点把与根节点之间的跳数看作自身的级别,节点的排序按照级别和ID标识的有序数对进行,遵循词典次序排列,具体过程如文献[16]所述。当所有的节点标记为灰色或黑色,根节点就开始执行下一阶段的算法。
4.2 分布式SCDT算法
下面介绍在有向图模型下的分布式 SCDT算法。算法运行在生成的极大独立集中的每个节点,分为2个阶段:①采用单源分布式dMST, dSPT和dDFS算法分别获取SPT,MST和DFS的遍历次序,在无向图模型中生成连通支配集;②通过改变与节点关联的边的方向反转每个节点所有的边,重复步骤①的过程。通过反转得到的SCDTD边的方向,生成反转的SCDTD′,联合2个阶段生成的SCDT,就得到强连通支配树。在构建过程中,节点之间使用消息WAKEUP、ADD、ADD_ FINISH、UPDATE、REVERSE实现信息交换。WAKEUP、ADD、ADD_FINISH 和 UPDATE消息如文献[16]所述,REVERSE消息如下。
REVERSE:如果节点收到该消息,反转关联的该节点的所有边的方向,把出边变为入边,把入边变为出边。
为构建SCDT树,分布式算法dSPT、dMST和dDFS在每个节点执行,发起和终止由根r控制,以串行方式运行,网络内的所有节点同步。按照dDFS过程中得到的顺序,首先在MSTT上执行算法,每个节点u使用p[u]记录上一级的父节点,d[u]记录距离。每个节点在初始时将d[u]设定为dT(r,u),根r依照dDFS所得次序,发布WAKEUP消息到后续的节点,发起遍历过程。
消息的传递触发以下处理规则。
1) 从节点v收到WAKEUP消息,节点u成为当前被访问的节点,u更新d[u]和p[u]。接着,u检查是否d[u]>αdSPT(r,u),若是,添加从r到u的路径PSPT(r,u)到T;否则,维持不变。为添加该路径,u发送给其在SPT中的父亲w消息ADD,这里,u是 ADD消息的发起者。接着,u等待发起者为u的ADD消息的回复。
2) 当节点w而不是根节点收到来自节点u的发起者i的ADD消息,w发送一个发起者为i的ADD消息给SPT中的父亲x,同时,w记录u作为新的子节点。
3) 当根节点r收到发起者为i的ADD消息,r记录u为新的子节点,并返回ADD_FINISH消息至u,与ADD消息一样,ADD_FINISH也需要包含发起者。
4) 当节点u收到w的发起者i的ADD_FINISH消息,节点u更新d[u]和p[u]。若u不同于i,u发送发起者为i的ADD_FINISH消息给向u发送发起者i的ADD消息的节点;否则,u向由dDFS获得的下一个节点发送WAKEUP消息,若p[u]由x变为y,u发送一个发起者为u的UPDATE消息到x。
5) 当节点x从u收到UPDATE消息,节点x更新d[x]和p[x]。若p[x]由v变为w,x发送一个发起者为x的UPDATE消息到v。
6) 若在dDFS所得序列中的最后一个节点u收到发起者为u的ADD_FINISH消息,就反转与自己关联的边的方向,并发送REVERSE消息给其父亲。
7) 每个节点在收到REVERSE消息时,反转所关联的边的方向,并发送REVERSE消息给自己的父亲节点。
在收到发起者为u的REVERSE和UPDATE消息,u被标记为dDFS队列中的最后一个节点。根r反转与其关联的边,结束第一阶段。然后r发送WAKEUP消息发起第二阶段。在根r收到一个发起者为u的UPDATE消息,而且u在dDFS次序中标记为最后一个节点时,算法终止。
5 理论分析及算例
把SCDT算法运用到图G,构造强连通树C,设γ=2且Cv=1,p(opt)为SDTT问题的最优解opt的总能耗。
引理1 在有向图G中,图G的支配树C总功率消耗p(C)≤w(G)。
证明

引理2 对于图G的SPTH和MSTT和T′,H的功耗至多倍MST功耗。
证明 由文献[5]证明知,

显然

由此得证。
引理3w(Topt)≤Δp(opt),w(T′opt)≤p(opt)Δ是G中最大节点度。
证明 由文献[16]可知,w(Topt)≤Δp(opt)。
对于T′,每个非根节点有且仅有一条出边,因此,w(T′opt) ≤p(opt),由此得证。
定理1 设C为由SCDT构建的SCDT-tree,那么
证明 设图G的SPTH,MSTT和T′,由引理1和2,可得

由此得证。
下面分析分布式算法 SCDT的时间和消息复杂度。
定理2 分布式SCDT算法的时间复杂度O(n2),消息复杂度O(n2)。
证明 由前面过程可知,在每个节点同时执行SCDT算法。ROUTE-ADD决定了算法的执行时间,而ROUTE-ADD的最大执行时间正比于RELEXed边数,而RELEX的执行时间是O(1)的。因此,考虑最坏的情况下,需要添加长度为O(n)的路径,这样ROUTE-ADD的执行时间为O(n),由于dSPT、dMST和dDFS等算法的时间复杂度最大为O(n2),显然算法SCDT的时间复杂度也为O(n2)。
在运行过程中,每个节点发送 REVERSE和WAKEUP消息 2次。ADD、ADD_FINISH和UPDATE至多O(n)次,因此算法总的消息复杂度应为O(n2)。由此得证。
下面给出SCDT算法执行过程示例。
在图1中,设图1(a)是执行MIS构建过程后形成的网络虚拟骨干节点的无向图,数字表示节点之间的通信距离;图1(b)是在考虑每个节点为实现有效的传输所需要的发送功率后,形成的一个强连通双向加权信息图,每边上的数字表示该方向上节点对间的通信所需的传输功率;图1(c)是边反转后的加权图;图 1(d)是最短路径树H,图 1(e)和 1(f)是最小支撑树T和T';设节点1为根节点,且α=2,对T按照DFS次序进行遍历,当访问4时,T中的路径(1,2,3,4)dT(1,4)=23,此时在H中,dH(1,4)=11,也就是dT(1, 4)大于2dH(1, 4)=22,于是把边(1,4)添加到H,同时p[u]从3更新为1。注意到边(3,4)没有删除,这是因为需要从此边回溯。在遍历T之后得到D如图1(g),同样的在遍历T'后得到D',如图 1(h),括号内的数字表示路径长度(即时延),外面的为该边的功耗,最后联合D和D'得到最终的SCDT树C,如图1(i)所示。

图1 SCDT-算法示例
接下来,验证算法的约束能力,分别单独计算图1所示MST、SDT和SPT的功耗:

以路径长度代替时延计算如下:
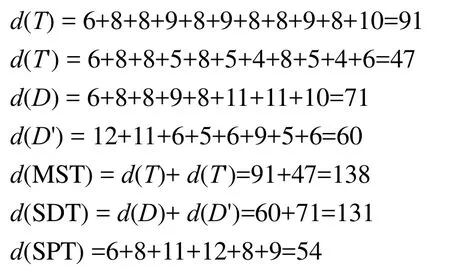
根据上面的计算结果可得:

结果表明SCDT算法执行正确,具有联合约束能力,符合预期效果。
6 仿真实验
采用与文献[16]相同的参数设置,在网络规模从20到300个节点的情况下进行仿真,所有的网络场景在1 000×1 000的单位区域内生成,对每个网络场景运行20此取统计平均值。对每条边e设置其权重为Cvdruv,dru为图G单位长度下的欧氏距离,r取值2。Cv为随机常量,由网络场景参数为每条链路设定。
图2的仿真结果表明,由于算法SCDT仅添加在最小支撑树中从u到r的权重2倍以上最短路径树中权重的路径,算法SCDT能量消耗低于SPT,有效限制了总能耗。另外,在固定区域范围内,当网络规模不断变大,节点数增多时,邻居节点之间的距离在逐渐变小,因此总能量消耗并没有快速增加。由图2(b)可知,就能量消耗而言,SCDT/MST要比 SPT/MST低,而且在固定的区域内,随着节点数增加,网络密度增加,此时节点彼此之间更加接近,分布更均匀,所以比值呈下降趋势,都更接近MST,也就是总能耗最小。
本文通过统计路径长度来简化传输时延特性分析。由图3可以看出,对路径长度而言,算法SPT总是最短也就是说传输时延最小,符合最短路径的特性。由图3(b)可知,就时延而言,SCDT与SPT的比值要比 MST低,而且在固定的区域内,随着节点数增加,网络密度增加,此时节点彼此之间更加接近,分布更均匀,所以比值呈下降趋势,都更接近SPT,也就是总路径长度最小,传输时延更小。

图2 能量消耗对比

图3 传输时延对比
综合图2和图3的结果可知,SCDT具有在最小费用MST和最短路径SPT之间的折中能力。
为分析α参数的选择对算法时延和能耗约束关系的影响,分别对不同α取值时SCDT、MST和SPT算法总能耗和路径时延进行仿真,结果如图4所示。为分析能耗关系,如图4(a)所示,分别把SCDT和SPT能耗与最小能耗MST进行比较。当α=1时,SCDT算法构建SPT,因此,2条曲线在1处相交,随着α得增加,SPT/MST保持在5左右;SCDT/MST逐渐降低,当α足够大时,此时对SCDT而言,只考虑能耗而不考虑时延问题,SCDT成为MST,符合的关系。
为分析传输时延关系,如图4(b)所示,分别把SCDT和MST总路径长度与最短路径SPT进行比较。当α=1时,SCDT构建 SPT,随着α的增加,MST/SPT维持在5;然而,SCDT/SPT逐渐增长,最后与MST相交。这是因为当α足够大时,基本不考虑时延约束,SCDT等同于构建MST。
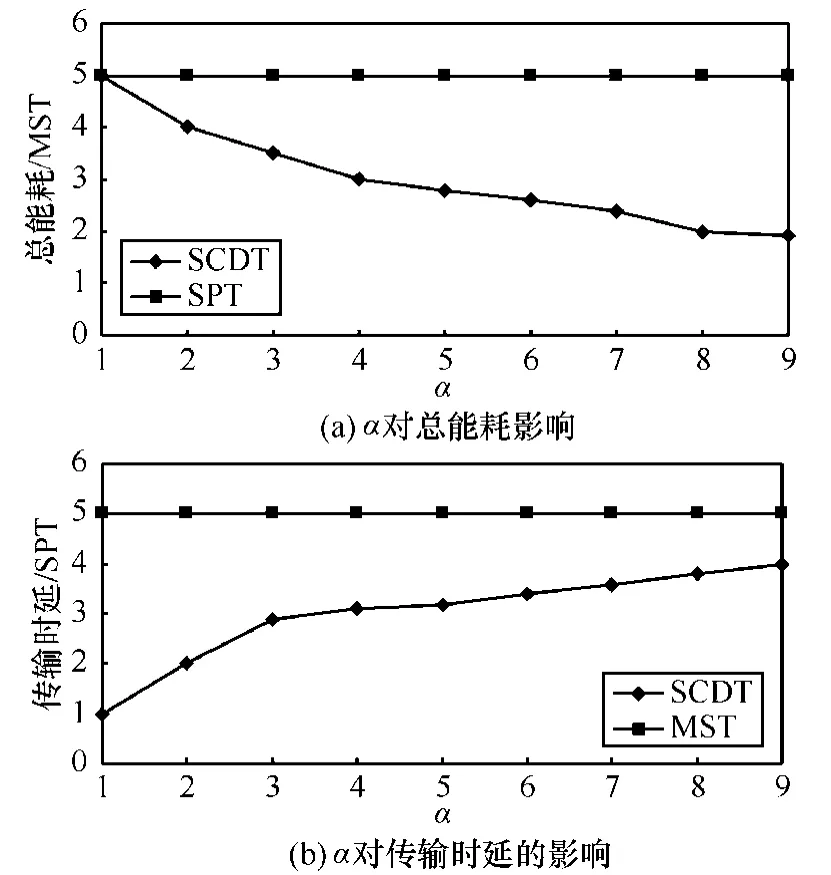
图4α对约束关系的影响
7 结束语
为了解决无线传感器网络虚拟骨干构造时能耗和时延联合约束的问题,考虑到无线链路的不对称性,借鉴平衡MST和SPT树的(α,β)约束机制,本文提出基于有向图构造时延和能耗均衡的强连通支配集的分布式算法,解决了能耗和时延均衡的问题。理论分析、算例和仿真实验都证明了提出的算法对解决该问题的有效性。在实际应用中,可以结合具体应用要求确定参数α、β调节约束关系。
[1] KIM D, WU Y, LI Y,et al. Constructing minimum connected dominating sets with bounded diameters in wireless networks[J]. IEEE Trans Parallel and Distributed Systems, 2009, 20(2): 147-157.
[2] MISRA R, MANDAL C. Minimum connected dominating set using a collaborative cover heuristic for ad hoc sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2010, 21(3): 292-302.
[3] ZHENG C, SUN S X, HUANG T Y. Constructing distributed connected dominating sets in wireless ad hoc and sensor networks[J].Journal of Software, 2011,22(5):1053-1066.
[4] 卞永钊,于海斌,曾鹏. 无线传感器网络中一种启发式最小连通支配集算法[J]. 信息与控制,2009, 38 (3): 355-359 BIAN Y Z, YU H B, ZENG P. A heuristic minimum connected dominating set algorithm for wireless sensor network[J]. Information and Control, 2009, 38 (3): 355-359.
[5] 徐洪兵, 祝颖. 基于拓扑控制的异类无线传感器网络分簇算法研究[J]. 电子科技大学学报, 2006, 35(4): 674-677.XU H B, ZHU Y. A topology-based cluster algorithm of heterogeneous wireless sensor networks[J]. Journal of University of Electronic Science and Technology of China, 2006, 35(4): 674-677.
[6] THAI M T, WANG F. Connected dominating sets in wireless networks with different transmission ranges[J]. IEEE Transactions on Mobile Computing, 2007, 6(7): 1-10.
[7] WU W L, DU H W, JIA X H,et al. Minimum connected dominating sets and maximal independent sets in unit disk graphs[J]. Theoretical Computer Science, 2006, 352(1): 1-7.
[8] 许力,林志伟. 基于图着色的无线自组网极小连通支配集算法[J].通信学报, 2007, 28(3):108-114.XU L, LIN Z W. Graph coloring based minimal connected dominating set algorithm in wireless ad hoc networks[J]. Journal on Communications, 2007, 28(3):108-114.
[9] 孙超, 尹荣荣, 郝晓辰. WSNs中基于能量代价的最小权和支配集拓扑控制算法[J]. 电子与信息学报, 2010, 32(4): 857-863 SUN C, YIN R R, HAO X C. Energy cost based topology control algorithm of minimum-total-weight connected dominating set in WSNs[J]. Journal of Electronics and Information Technology, 2010,32(4): 857-863.
[10] 汪文勇, 向渝, 董传坤等. 用马尔科夫模型优化分布式最小连通支配集算法[J].电子学报,2010, 38(10):2441-2446.WANG W Y, XIAGN Y, DONG C K,et al. Optimizing distributed algorithm for minimum connected dominating set with Markov model[J]. Acta Electronica Sinica, 2010, 38(10):2441-2446.
[11] 王玉明, 赵大胜. 基于串行最大独立集的连通支配集构造及分析[J].华中科技大学学报(自然科学版),2011,39(3):61-65.WANG Y M, ZHAO D S. Construction and analysis of connecteddominating set based on serial maximum independent set[J]. Journal of Huazhong Science and Technology (Natuaral Science Edition),2011,39(3):61-65.
[12] 郑杰, 郭淑杰, 屈玉贵等. 无线传感器网络能效时延平衡数据收集机制[J].中国科学技术大学学报,2008, 38(12):1414-1421.ZHENG J, GUO S J, QU Y G,et al.Energy efficiency and delay balancing data gathering for wireless sensor networks[J]. Journal of University of Science and Technology of China, 2008, 38(12):1414-1421.
[13] 郜帅, 张宏科. 时延受限传感器网络移动Sink路径选择方法研究[J]. 电子学报,2011, 39(4):742-747.GAO S, ZHANG H K. Optimal path selection for mobile sink in delay-guaranteed sensor networks[J]. Acta Electronica Sinica, 2011,39(4):742-747.
[14] SAMIR K, BALAJI R, NEAL E. Young balancing minimum spanning trees and shortest path trees[J]. Algorithm, 1994, 120(4):305-321.
[15] LI Y S, THAI M T, WU F. On the construction of a strongly connected broadcast arborescence with bounded transmission delay[J].IEEE Transactions on Mobile Computing, 2006, 5(10):1460-1470.
[16] 孙彦景, 钱建生, 顾相平等.联合约束无线传感器网络连通支配集算法[J].电子科技大学学报,2009,38(2):231-235.SUN Y J, QIAN J S, GU X P,et al. Distributed connected dominating set algorithm with combined constraints in wireless sensor network[J].Journal of University of Electronic Science and Technology of China,2009,38(2):231-235.
[17] LI Y, CHENG M X, DU D Z. Optimal topology control for balanced energy consumption in wireless networks[J]. Journal Parallel and Distributed Computing, 2005, 65(2): 124-131.
[18] WAN P J, KHALED M A, OPHIR F. Distributed construction of connected dominating sets in wireless ad hoc networks[J]. ACM/Kluwer Mobile Networks and Applications, 2004, 9(2): 141- 149.

