非线性算法在近红外预测木材密度中的应用研究

李耀翔，张鸿富

(1.东北林业大学工程技术学院，哈尔滨150040;2.云南农业大学，昆明650201)

木材是一种复杂的天然有机聚合物，主要由木质素、纤维素、半纤维素和一定数量的抽提物等高分子有机物组成，这些组分在近红外谱区都有较强的吸收度，这使得近红外光谱技术预测木材的密度成为可能。木材密度是木材性质的一项重要指标，根据木材的密度信息可以估计木材的重量、判断木材硬度、强度等物理力学性质及工艺性质。传统的测量木材密度的方法费时且费力，对其进行快速、准确的预测具有十分重要的意义。近红外光谱分析技术具有操作简单、预测结果准确、对试样无损等优点，在国内外已广泛用于检测木材密度、强度、含水率、木质素、抽提物、糖类等物理及化学性质［1－3］。落叶松作为我国东北林区大量种植的重要用材林树种，具有种植范围广，木材蓄积量大的特点，用近红外光谱分析技术对其密度进行预测有利于提高落叶松木材的利用率。本文运用基于高斯核变换的非线性偏最小二乘法结合近红外光谱，对木材密度进行了预测研究［4］。

1 样品的制备与数据采集

本次试验所用落叶松试材采自黑龙江带岭林业局东方红林场，北纬 46°50'8″～ 46°59'20″，东经128°57'16″～129°17'50″，海拔 650m。在所选标准样地中从背阴面及向阳面各选一株健康木作为标准木。所选标准木直径分别为26.2 cm和26.3 cm，树高分别为23.2 m和23 m。在每株标准木的胸高(1.3 m)附近连续截取5 cm厚圆盘，带回实验室将每个圆盘去皮后过髓心纵向取20 mm×40 mm×200 mm样条，每个样条取规格为20 mm×20 mm×20 mm样方，总计117个样方。落叶松木材气干密度的测量按照《木材物理力学性质试验方法》(GB1933－1991)进行。运用MATLAB 7.0编写程序将117个样品按照3∶1的比例随机分为校正集和验证集，其中校正集共88个样品，验证集共29个样品。具体信息见表1。

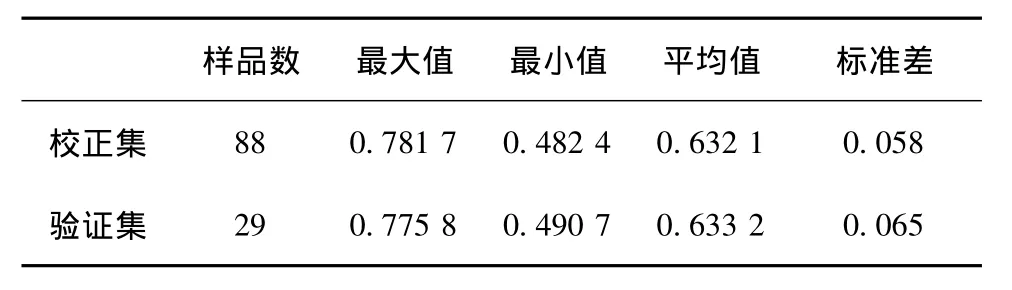
表1 样品密度统计信息Tab.1 Statistics of wood density for the samples (g/cm3)

样品近红外光谱的采集仪器采用美国ASD公司生产的LabSpecR Pro FR/A114260便携式快速扫描光谱仪。该仪器光谱波长范围为350～2500 nm，光谱分辨率为3 nm@700 nm，10 nm@1 400和2 100 nm。实验室温度、湿度基本恒定，室内温度控制在20±1℃，平均相对湿度为50%。采集样品光谱前先用聚四氟乙烯制成的白色材料进行空白校准，由于用近红外光谱分析技术分析木材密度时在木材横切面、径切面、弦切面3个切面中对横切面采集的光谱建模预测效果最好［5］，本次实验采用两分叉光纤探头垂直于样品的横切面采集光谱。在全光谱范围内对样品进行扫描，设置波长范围每隔10 nm纪录一个信息点，每个样品扫描30次并自动平均为一个光谱，每条光谱共得216个信息点［4］。

2 数据分析与建模

2.1 基于高斯核变换的非线性偏最小二乘法建立落叶松密度模型

设自变量光谱信息点x1，x2，…，xp与因变量样品密度值y的函数关系式为

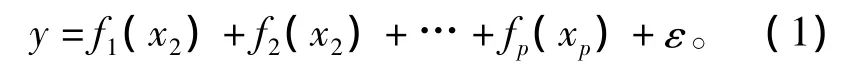
设fj(xj)的核函数变换为^fj(xj)(j=1，2，…，p)，则有

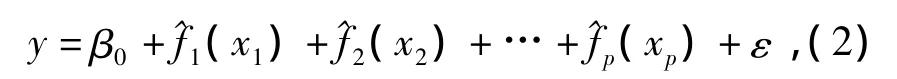
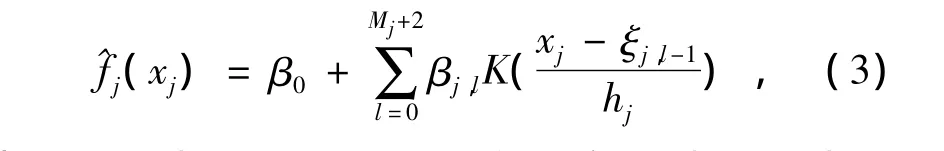
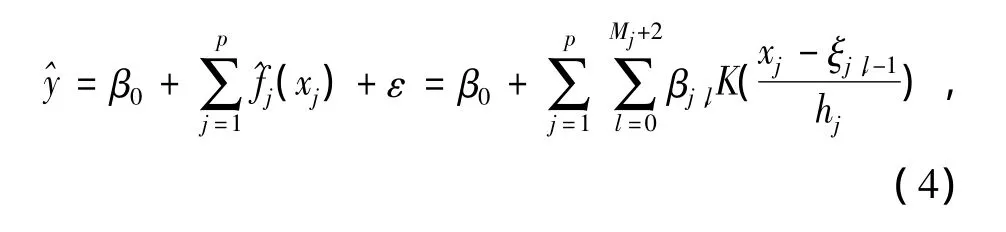
式中:ξj，l－1为变量 xj上划分的区间分点，hj为分段长度、Mj为分段个数，进而可以得到全体光谱信息矩阵与密度矩阵的非线性拟合函数可表示为式中:y 与 zj，l=K之间是线性关系，可以用求解线性回归的方法对其构造回归模型，需要注意的是在进行变量替换后新的变量之间也可能存在多重共线性，可以采用偏最小二乘方法进行模型的求解来消除多重共线性的影响。

2.2 Bootstrap方法对光谱信息变量筛选

在近红外光谱技术中由于光谱信息点的个数比较多，有时多达2 000个以上，大部分的光谱信息点之间存在着多重共线性，有的对所测性质而言可能是冗余信息，将其加入模型中可能还会降低模型的预测精度，同时使建模时间增长，使模型的泛化能力变差。本文采用Bootstrap方法对光谱信息进行筛选，去除冗余光谱点。Bootstrap变量筛选方法是1979年由美国斯坦福大学统计系教授倚佛侬提出的一种基于数据模拟的再抽样方法，也称为自助法，Bootstrap方法在运用过程中只依赖于给定的样本信息，而不需要其他假设或增加新的样本，是一种新的变量筛选方法［6－11］。

3 模型的评价

本文用于评价模型质量的参数主要有相关系数(R)，均方差根误差 (RMSE)及平均精度(PRE)。相关系数 (R)，其取值范围在 ［0，1］，其值越大，模型拟合就越好:

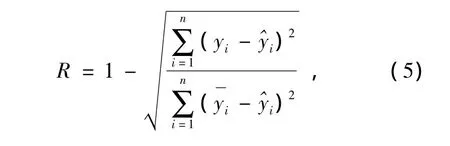
式中:n为建模的样本数，yi为实验室运用标准方法测定的实际值，为所建模型的预测值，为实验室运用标准方法测定实际值的平均值。

均方差根误差 (RMSE)，均方差根误差越小，模型拟合效果越好:

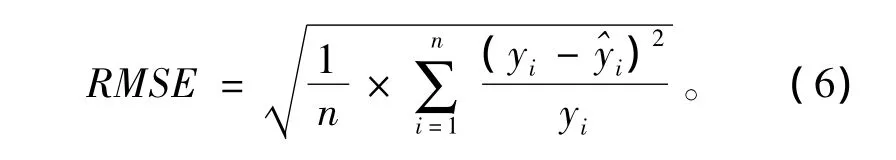
平均精度 (PRE)，平均精度越大，模型拟合性越好。

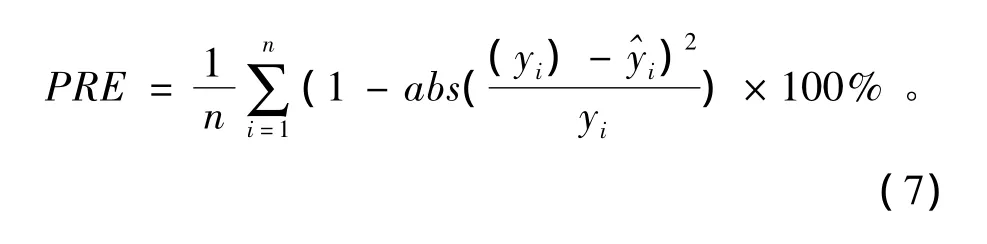
4 结果与讨论

4.1 光谱数据的处理

将所采集的光谱进行卷积平滑和一阶导数处理以消除背景噪声及基线的影响。为了减少自变量的个数，提高运算速度及建模精度，所得光谱的216个信息点采用Bootstrap方法筛选变量 (本文所采用Bootstrap方法、线性与非线性偏最小二乘建模方法程序均由MATLAB 7.0编写)，第一次设置检验水平α=0.15，取B=100，有83个自变量未通过显著性检验，将其剔除，剩余133个光谱数据。第二次设置检验水平α=0.1，取B=100，有71个自变量未通过显著性检验，将其剔除，剩余62个光谱数据。第三次设置检验水平α=0.1，取B=300，有41个自变量未通过显著性检验，将其剔除，剩余21个光谱数据。第四次设置检验水平α=0.05，取B=100，有6个自变量未通过显著性检验，将其剔除，剩余15个光谱数据。再次设置检验水平α=0.05，取B=100所有变量均通过检验，最后通过Bootstrap方法筛选最后剩余15个光谱信息点用于线性和非线性偏最小二乘法的模型构建。

4.2 主成分数的选择对模型的影响

在运用非线性偏最小二乘法建立模型时，为了选择最佳主成分数，使所建模型能够在最大程度上反映样品密度值与光谱数据之间的关系，图1和图2分析了随着主成分数的增加模型RMSE与PRE变化关系。从图1可以看出随着主成分数的增加，校正集RMSE逐渐下降，在主成分数为10时趋近于0.02，而验证集RMSE在主成分数在1至5之间呈现下降趋势，而在5以后却又呈现上升趋势，在主成分数为5处出现了拐点。图2中随着主成分数的增加，校正集PRE逐渐升高，在主成分数为10时趋近于97.5%，而验证集PRE在主成分数在1至5之间呈现上升趋势，而在5以后却又呈现下降趋势，在主成分数为5处出现了拐点。从图1及图2可以看出校正模型的拟合能力随着主成分数的增加而增强，但是预测能力却是随着主成分数的增加出现了先增强后减弱的现象，所以综合校正集及验证集两方面的考虑，确定5为最佳主成分数，基于主成分数为5建立的校正模型拟合能力及预测能力为最优。

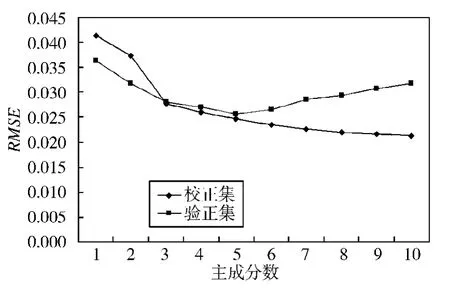
图1 非线性偏最小二乘回归主成分数与均方差根关系图Fig.1 The relationship between number of principle components and RMSE with nonlinear PLS

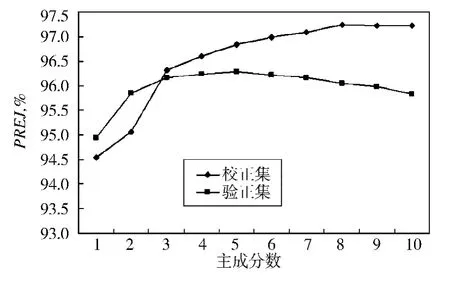
图2 非线性偏最小二乘回归主成分数与平均精度关系图Fig.2 The relationship between number of principle components and PRE%with nonlinear PLS

4.3 线性与非线性偏最小二乘法建模对比分析

在确定了最佳主成分数后，运用非线性偏最小二乘法 (主成分数为5)构建落叶松木材密度近红外光谱模型，建模结果与传统线性偏最小二乘法进行了对比 (见表2)。通过表2可以看出，从对落叶松样品密度预测方面，无论非线性偏最小二乘法所建模型还是线性偏最小二乘法所建模型都能实现有效预测。但从模型的具体参数比较来看，非线性偏最小二乘法所建模型不论校正集还是验证集的相关系数和平均精度都高于线性偏最小二乘法所建模型，均方根误差都小于线性偏最小二乘法所建模型，这说明了在结合近红外分析技术预测木材密度中非线性偏最小二乘法所建模型要优于线性偏最小二乘法所建模型，预测结果更加准确。还在一定程度上也反映了样品近红外光谱信息与样品的实际密度值之间不是单纯的线性关系，非线性关系可以更好地表征二者之间的关系。

表2 线性与非线性偏最小二乘法结果分析Tab.2 Comparison of modeling results with linear and nonlinear PLS

5 结论

本文给出了结合非线性偏最小二乘法应用近红外光谱技术对落叶松木材的密度的预测模型，并进行了模型比较。结果表明近红外分析技术可以快速、准确地预测木材的密度。

为了消除光谱信息中可能出现的冗余信息，提高建模的运算速度，对所采集的光谱运用Bootstrap变量筛选方法对光谱信息数据进行了降维，设置相关参数，经过4次筛选，一条光谱的216个信息点筛选剩余15个信息点作为一个样品的光谱信息，这就有效地提高了建模的运算速度及建模精度。

分别运用基于高斯核变换的非线性偏最小二乘法和传统偏最小二乘法建立密度预测模型，并且对所建模型的评价参数进行了对比分析。结果表明两种方法建立的预测模型都能对样品的密度进行有效预测，而在模型的具体参数比较上看，基于高斯核变换的非线性偏最小二乘法所建模型预测准确度要优于传统偏最小二乘法建立模型，这在一定程度上也反映了样品近红外光谱信息与样品的实际密度值之间不是单纯的线性关系，非线性关系可以更好地表征二者之间的关系。

［1］黄安民，江泽慧.近红外光谱技术在木材性质预测中的应用研究进展［J］.世界林业研究2007，20(1):49－54.

［2］严衍禄，赵龙莲，韩东海，等.近红外光谱分析基础与应用［M］.北京:中国轻工业出版，2007.

［3］陆婉珍，袁洪福.现代近红外光谱分析技术［M］.北京:中国石化出版，2007.

［4］张鸿富.基于近红外光谱技术的落叶松木材材性预测的研究［D］.哈尔滨:东北林业大学，2011.

［5］江泽慧，黄安民，王 斌.木材不同切面的近红外光谱信息与密度快速预测［J］.光谱学与光谱分析，2006，26(6):1034 －1037.

［6］王惠文，吴载斌，孟 洁.偏最小二乘回归的线性与非线性方法［M］.北京:国防工业出版社，2006.

［7］Nguyen H T，Lee B.Assessment of rice leaf growth and nitrogen status by hyperspectral canopy reflectance and partial least square regression［J］.European Journal of Agronomy 2006，24:349 － 356.

［8］琚存勇，邸雪颖，蔡体久.变量筛选方法对郁闭度遥感估测模型的影响比较［J］，林业科学，2007，43(12):33 －38.

［9］杜晓明，蔡体久，琚存勇.采用偏最小二乘回归方法估测森林郁闭度［J］，应用生态学报，2008，19(2):273 －277.

［10］孟宪静，孙天用，王立海.基于红外热像技术的木材内部缺陷检测的研究［J］.森林工程，2011，27(6):33 －35.

［11］张 莉，周金池.近红外光谱检测技术及其在木材工业中的应用［J］.林业机械与木工设备，2010，38(10):4 －6.