基于马尔科夫随机场模型的多视角异质多模图像的目标检测

何智翔 丁晓青

（智能技术与系统国家重点实验室，清华信息科学与技术国家实验室，清华大学 电子工程系，北京100084）

在医学和高空目标观测等领域，存在大量的不同光质多模图像之间的目标检测问题。因为在这些领域中，存在大量不同感光成像设备生成的图像，我们称这些图像为异质多模（multimodal或者 multisensor）图像［1，2］。

在有关异质多模图像的研究中，Ma Jun和Zeng等［3，4］利用 sobel算子生成原图像的边缘图，然后利用边缘图的互相关进行匹配。参考图像和观测图像虽然光质不同，但是处于同一视角并且是同一场景，背景比较简单。类似的方法也出现在了文献［5，6］中，也是边缘图被用来进行配准；不同的是，参考图像和观测图像不是同一视角；但是因为规定图像间只有有限的平移、旋转、尺度变换，所以通过简单的仿射变换就可以消除。Cheng和Zheng等［7］则不使用边缘图，而是利用SVM从提取到的边缘中抽取物体的轮廓，然后使用hausdorff距离进行轮廓匹配。Manjunath和Huang［7，8］也使用轮廓，但他们使用其他方法来提取轮廓并匹配它们。此外，在文献［7－9］的研究中，它们的参考图像和观测图像虽然是同一场景，但背景并不严格一致，视角也不完全相同，但是相差不多。此外，在最近的研究中，如 Michael和Krotosky等［2，10］，尝试利用三维场景数据对异质多模图像进行配准，不是简单的图匹配。这些研究，大多都是针对异质多模图像的配准，通过配准来检测目标。

本文研究的主要对象是不同视角的异质多模图像，参考图像和观测图像之间除了光质不同外，还具有以下2个主要的困难：首先就是参考图像和观测图像的视角不同，仿射变换无法完全消除其影响；其次就是参考图像和观测图像包含复杂的背景，我们采用的实验数据是可见光俯视参考图像和红外光侧视观测图像，如图1所示。其中三维物体的高度信息导致了场景不一致且红外光观测图的清晰度低，受到了噪声强烈的干扰。

图1 本文研究所使用的数据Fig.1 Image data used in this research

就我们所知，现有的这些研究［3－9］的实验数据都具有不太复杂的背景（噪声少，场景比较相似等）以及相近的视角，所以他们的方法可能不能很好地处理这种情况。

不同于前面提到的研究［3－9］，本文不使用基于边缘的特征。因为依赖于边缘的方法，容易受到图像中噪声和视角不同所带来的影响，特别是对于本文研究的低清晰度红外观测图。而本文采用的区域特征对于视角变换可能引起的形状畸变和噪声的干扰更加鲁棒，相对比较稳定。

最终，本文在贝叶斯最小风险理论的指导下，利用马尔可夫随机场（Markov Random Field或MRF）模型来描述在异质多模图像中用MSER［11］的方法提取得到的地面稳定区域特征之间的空间约束关系及统计特性，通过配准异质多模图像实现最终的目标检测。

1 相关的工作

1.1 MRF模型

马尔可夫随机场是建立在马尔可夫随机链的基础上的，在MRF中，当前位置的状态只与相邻位置上的状态有关。MRF模型提供了不确定性描述与先验知识联系的纽带，并利用观测图像，根据统计决策和估计理论中的最优准则确定目标函数。

利用MRF模型，我们能够建立基于图像中的地面稳定区域特征的图模型，从而可以依赖于图模型的配准进而在观测图像中检测甚至定位参考图像中的目标。

1.2 MSER区域提取

通过比较图1中的参考图像和观测图像，我们可以得到关于异质多模图像的一些特点。首先，异质多模图像中的同一物体区域由于图像模式不同，会呈现出不同的纹理特征；而由于同一场景中的不同物体存在各自的变化规律，因此也很难通过类似于光照变化的调整方法来消除这种差异。其次，虽然物体的纹理不一致，但是它们的大致形状是相似的，特别是在同一视角之下。

正是由于形状是异质多模图像间最稳定的特征，现有的一些基于纹理的特征并不适用于异质多模图像的目标检测，而需要使用与物体形状相关的特征。以HOG特征为例，如图1中的广场，因为纹理特征不一致，在局部区域上计算HOG特征，会发现两者的梯度强度和方向都不一致，从而导致检测失败。

在文献［11］中，Matas通过将注水算法引入连通域提取的过程，从而得到了一种有效的提取稳定区域的方法，称为最大稳定极值区域提取（Maximally Stable Extremal Regions，简 写 为MSER）。由于MSER选取的是那些形状在一定步长的灰度变化下不敏感的区域，因此它能够有效地克服噪声的干扰，提取在不同图像模式下形状足够稳定的物体区域，比如湖泊、广场、水田等。因此，MSER可以被用来提取异质多模图像中的稳定物体区域来描述物体的形状。

1.3 RANSAC算法

在最后的目标检测过程中，需要寻找一组从观测图像中提取的区域配准图模型。我们采用RANSAC［12］的思想来寻找这个最佳配准。

简单说来，RANSAC算法就是一种从样本中准确拟合数学模型的算法，包括去除噪声点（野值）和留下有效值等等，采用随机抽样验证的方法。它利用已知模型，从样本集中随机选取若干个点，并拟合模型参数，然后根据参数将样本集中的点添加入候选集合，直到误差小于阈值或者候选集合中的点满足一定的数目要求。采用RANSAC算法可以从可能的与模板匹配的物体区域集合中快速寻找和图模型的最佳匹配，而不必使用穷举算法去遍历每一个可能的组合与图模型的配准结果。

1.4 Hausdorff距离

常用的利用边缘特征进行匹配的算法是Hausdorff距离［7，13］。在前面介绍的利用边缘特征对多模图像进行匹配的研究中，Cheng和Zheng［7］使用该算法来衡量多模图像中边缘的相似程度。

Hausdorff距离属于一种边缘匹配测度，它以2个边缘之间的最大的最小距离作为度量，能够较好地克服噪声的干扰；但是对模板形状的要求比较高。正是因为基于边缘特征的方法对于形状不一致比较敏感，本文最终选择了利用 MSER提取稳定区域的方法，通过计算二值连通域的互相关值来进行匹配。尽管利用 MSER在异质多模图像中提取的同一物体的稳定区域也并不一定能保证形状完全一致，但是在利用给定的摄像机外部参数进行视角变换的情况下，足够保证模板与对应区域的正确匹配。

在第4节，我们将给出本文的利用区域特征匹配的方法和文献［7］中采用Hausdorff距离进行边缘特征匹配的方法的实验结果对比。

2 基于MRF模型的目标检测方法

我们的目标检测方法的核心是利用 MSER提取物体区域，然后在MRF模型的基础上进行匹配。前面已经提到过我们为什么选择区域特征而不是边缘特征来描述物体的形状，在这里我们将给出更加详细的解释，主要是以下3点理由：首先是观测图像的清晰度很低，噪声的干扰非常严重，物体的形状很难依靠边缘特征进行准确的描述；其次是缺乏精确的视角变换参数，不能通过变换使同一物体的形状完全一致；最后因为使用MSER的方法来提取不同模式图像中的同一物体，使用区域特征更加适合。

2.1 MRF模型

由于观测图像与参考图像视角的差异极大，尤其是参考图像为俯视图而观测图像为侧视图，因此，图像中物体的高度信息会对检测产生极大的干扰。为了降低物体的高度信息对检测的影响，我们选择那些高度信息可以忽略的地面物体作为稳定区域特征，并利用这些地面区域特征作为对图像的描述。

于是在贝叶斯最小风险理论下，地面稳定区域看做是图像上的前景RFG，而其他区域则是背景RBG。于是图像I＝RFG∪RBG且RFG∩RBG＝∅。地面稳定区域在图像中的位置L＝（l1，l2，…，ln），那么前景图像的条件概率分布为

背景图像的条件分布概率为

最优的配准结果为

（3）式直接求解是困难的。

但是在MRF模型的框架下，图像中的相邻地面物体区域之间存在联系，于是可以用一个统一的模型描述地面物体区域的结构约束和地面物体区域的统计特性。

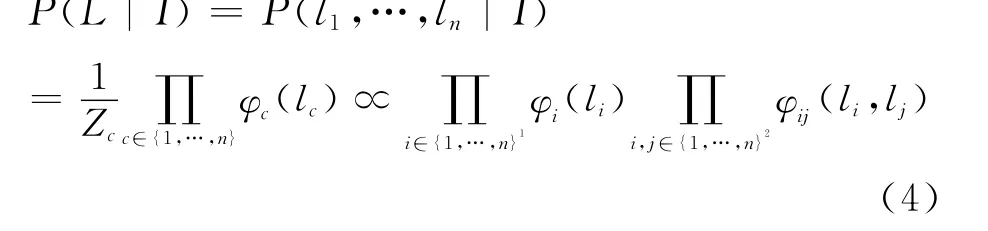
似然概率为

由（5）式可知，似然概率可以转化为下式：

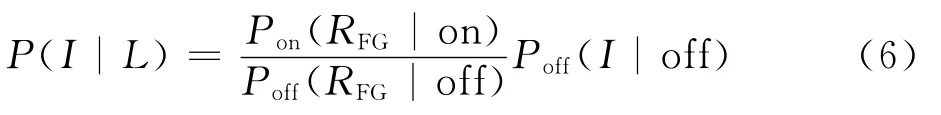
由于抛开空间位置约束，各个稳定区域可以认为是相互独立的，所以（7）式成立

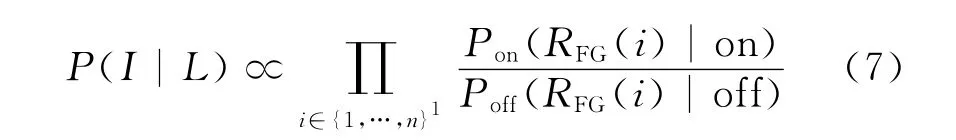
令

于是

其物理意义在于，最优的图模型匹配结果要求在观测图像中匹配上的地面稳定区域为参考图像上的前景的概率越大越好，为背景的概率越低越好，且满足空间约束的概率要高。

基于该模型，我们的方法的基本步骤如下。

首先进行视角变换，因为多模图像间最稳定的特征是与形状相关的特征，而参考图像和观测图像之间的视角差异太大，必须将它们变换到相近的视角上，这样才能利用形状来进行匹配。

接下来，MSER被用来提取参考图像和观测图像中的物体稳定区域。之后，参考图像中的在地面上的物体稳定区域被选为模板（前景图像），并构建MRF模型。

最后，通过计算稳定区域之间的近似程度，建立每个模板在观测图像上的候选匹配区域集合，并按照（9）式，在满足空间位置约束的情况下选取最优的匹配。

2.2 视角变换

在本文的研究中，由于摄像机的视角参数已知，所以我们直接利用给定的摄像机视角参数将观测图像变换到俯视的视角上。不变换到侧视图中是因为视角变换的误差在侧视图中很难通过简单的旋转和缩放消除，如图2所示。

图2 参考图像变换与观测图像变换的比较Fig.2 The comparison between the transformation results of reference image and sensed image

从图2还可以看到，视角变换确实对存在高度信息的物体形状产生了很大的影响，因此，我们抽取合适的地面物体区域作为模板。

2.3 稳定区域提取

视角变换后，我们将利用MSER提取图像中的稳定区域。由于MSER算法提取稳定区域的特点，它只能够提取灰度小于某个阈值或者大于某个阈值的区域。为了能够充分利用MSER，我们引入了图像灰度变换。

本文不仅仅在原图像I中提取了稳定区域，还在反色图像Irev以及利用公式（10）和（11）进行灰度变换后的图像Itra中提取了稳定区域。图3显示了灰度变换后的参考图像，对于观测图像也是如此。I（x，y）是图像上位于（x，y）处的灰度值，b为图像的宽度，h为图像的高度。

图3 灰度变换后的图像Fig.3 The gray transformation of an image

从参考图像中得到的这些地面稳定物体区域将被看做前景图像用来建立图模型以描述目标，而从观测图像中提取到的稳定区域则被作为待匹配的物体区域，如图4所示。从每个模板中提取特征，加上对应的几何约束，就构成了参数化的图模型描述。

图4 参考图像和观测图像中提取的MSERFig.4 The stable regions extracted from the images

2.4 模板和稳定区域的距离

在匹配模型之前，我们需要计算从观测图像中提取的稳定区域与每个模板之间的距离dcorr来衡量它们之间的形状相似程度。该相似程度反映了公式（9）中概率的大小。在本文中，我们使用最简单的互相关方法（CC），如（12）式所示。其中，T为模板对应的二值图，I为观测图像中提取的稳定区域对应的二值图。ST是T中前景像素的面积，SI则是I中前景像素的面积。

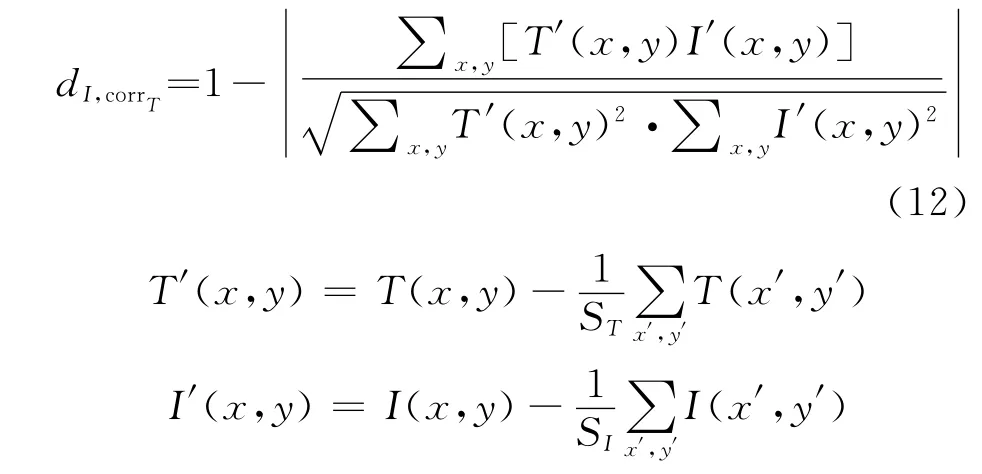
在得到第i个模板与观测图像中提取到的第j个稳定区域的距离dj，corri以后，如果

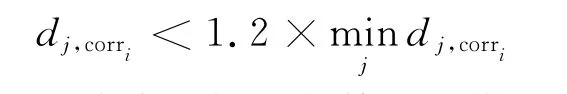
那么第j个区域将被加入与第i个模板对应的第i个候选匹配区域集合中。

图5是随机选取的2个模板的匹配结果示意图，其中，灰白色区域表示的是模板的候选匹配区域集合在观测图上的位置。在这2个模板的匹配结果中，有91.06%的正确匹配区域包含在该模板对应的候选区域集合中，而只有71.64%的正确匹配区域的dcorr最小。按照直接模板匹配的方法，最终的检测率将很难达到80%。

2.5 图模型的配准

图5 观测图像和与模板匹配的稳定区域Fig.5 Matching result of the codewords

最后我们将利用RANSAC的思想对图模型进行配准，并实现最终的目标检测。因为我们的模型不仅已知，而且参数确定，同时进行了2次随机抽样过程，所以我们的配准方法称为模型确定二 次随机抽样一致性算法MDQRANSAC（model determinate quadratic RANdom sample consensus）。

对于MDQRANSAC算法，模型参数不需要通过随机选取的数据去拟合，它是用来判断一组随机选取的数据是否满足约束的。而2次随机抽样过程分别是对模板集合的随机抽样和对模板的候选正确匹配区域集合的随机抽样。

我们首先随机选取2个模板，然后从选取的模板所对应的候选正确匹配区域集合中随机选取区域。这样可以选出2个区域，分别对应2个模板。然后我们利用模板的几何位置，计算选取的稳定区域的几何位置误差epos。

由于模板的几何位置采用极坐标表示，因此θi和ρi是第i个模板的位置，而θji和ρji是与第i个模板对应的稳定区域j的位置。几何位置误差ej，posi反映了 MRF模型中的结构约束的大小。如果ej，pos大于一个i事先确定的阈值tposi，区域j将被认为不满足MRF模型，需要重新选取i和j加入初始候选集合Scorr。

接下来根据MRF模型可以得到计算候选集合与图模型的归一化误差enormal的公式（14）

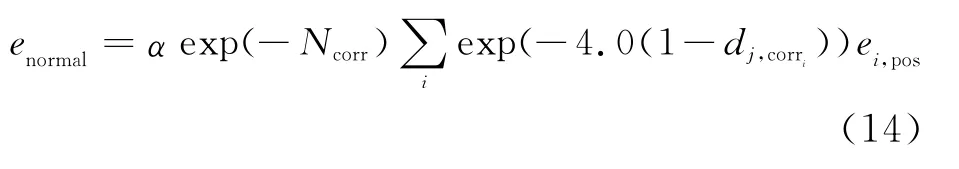
其中Ncorr是Scorr中区域的个数，α是一个保证归一化误差最大值为1的约束量，显然，α与tpos有关。我们使用下面的公式计算α，Ntemplate是图模型中包含的模板个数。

在（14）式中，之所以使用 exp（－4.0（1－dj，corri））作为ei，pos的权值，是因为当 dj，corri＝ 0时，该模板匹配到了正确的区域。但是在实际检测中，正确的匹配区域对应的epos不一定最小，导致enormal也不一定最小。因此，需要在epos之前乘以一个权值exp（－4.0（1－dj，corri）），使得已经确定的正确匹配区域得到enormal最小。

接下来与原RANSAC算法相同，随机选择模板再随机选择对应区域，不断有区域被加入Scorr。如果enormal＜ebest，那么Sbest将被更新为当前的Scorr；如果ebest小于一个阈值tpos或者到达循环次数的上限，算法停止；如果不规定循环次数上限且没有ebest＜tpos，那么算法将退化为穷举算法，遍历所有的对应。

当算法停止后，此时在Sbest中得到的将是与图模型的距离最近的配准结果；如果Sbest不存在，就认为观测图像中的目标不存在。另外，在MDQRANSAC中，并没有对满足模型参数的区域个数的要求，只要存在稳定区域被添加进候选集合，算法就会计算enormal。

显然，我们提出的算法也可以被应用在其他模型确定且存在多个对应，要求寻找最佳匹配的研究中，只是模型参数、各种误差约束的计算方法等，根据应用的不同会有所改变。

3 实验结果

在我们的实验中，参考图像为2幅可见光俯视图，而观测图像则为4组红外光侧视图序列，总共1 573幅图像，每2组序列对应1幅参考图像。其中的一幅参考图像和对应的1幅观测图像如图1所示。此外，数据中还包括与每幅观测图像相对应的摄像机的视角参数。

根据我们的方法，给出了最终的目标检测结果。每个参考图像都利用MSER提取了5个模板用来建立图模型，平均每个模板对应10个左右的稳定区域。如果遍历所有可能的组合，大约需要循环6 631 000次；但在MDQRANSAC算法中，规定了循环次数的上限为1000次。Intel Xeon在3.20GHz CPU，5.98GB内存的计算机上使用单线程处理，MDQRANSAC算法的平均处理时间为15ms。

首先给出使用我们的方法与直接利用模板进行区域匹配的方法的比较。直接利用模板计算相关的方法将首先计算每个模板与观测图像的互相关矩阵，然后选取观测图像上与模板相关度比较大的几个对应位置，最后利用MDQRANSAC按照几何位置关系搜索最终匹配结果，如表1所示。

表1 本文的方法与直接模板匹配的比较Table 1 The comparison of the method used in this study and model matching

可以看到，利用MSER提取物体稳定区域的方法克服了噪声的影响，获得了物体准确的形状描述，提高了最终结果的识别率。而在原观测图像上直接进行模板匹配的方法受到噪声的干扰以及灰度变化的影响，识别率较差。这从一个方面说明了利用 MSER提取稳定区域方法的有效性，能够提高区域正确匹配的准确率。

为了说明区域特征的优点，接下来给出的是采用区域特征的实验结果和采用边缘特征的实验结果对比，如表2所示。其中边缘特征的结果是用观测图像的边缘图和模板的边缘，通过计算Hausdorff距离得到。为了保证实验条件的一致，区域特征的方法也直接利用模板在观测图上计算互相关得到。最终的结果包含了从参考图上提取的全部模板的匹配结果。

表2 区域特征匹配与Hausdorff的方法比较Table 2 The comparison of the region feature matchingand the Hausdorff

从实验结果来看，基于区域特征的方法有效克服了存在的噪声以及视角变换不准确带来的误差。而基于边缘特征的方法则没有取得很好的实验结果。因为观测图像的清晰度很低，存在大量噪声边缘，同时形状的不完全一致也影响了匹配的性能。序列2基于边缘的结果要好于基于区域的结果是因为存在一个模板的匹配准确率只有5.56%，拖累了本文方法最终的匹配结果。

表3最后给出采用将观测图像进行视角变换与将参考图像进行视角变换的检测结果对比。

表3 不同图像视角变换的比较结果Table 3 The comparison of different view transformations

从实验结果来看，对观测图像进行视角变换得到的结果的识别率更高。因为变换到俯视的视角上，模板与对应的稳定区域之间只存在简单的旋转和尺度误差，对区域特征的匹配结果影响较小；而变换到侧视视角上，模板与稳定区域之间存在仿射畸变，对最终匹配结果的影响较大。其中，序列2对参考图像进行变换后，由于视角误差，变换后的区域的朝向与观测图像明显不一致，导致了最终的识别率很低，如图6所示。灰白色为模板在观测图像中的匹配位置。

图6 序列2的匹配结果Fig.6 Matching result of Group 2

而序列3和序列4由于摄像机的视角参数相对比较准确，因此得到了较高的检测率（80%以上）。

图7是使用我们的方法得到的一个检测结果（灰白色区域）。从参考图像中提取得到的模板总共有5个，但是最终的检测结果中，仅仅依靠其中3个，就保证了观测图像与图模型的距离小于阈值。

4 总结

本文通过匹配地面物体区域，将三维目标的匹配问题转化为了二维的图匹配问题，为解决不同视角下具有复杂背景的异质多模图像的目标检测，提供了一个新的方法。

图7 检测结果Fig.7 Target detection result

从实验结果对比来看，本文基于物体区域特征匹配的方法确实获得了比边缘特征更加优异的检测性能。同时采用MSER来提取稳定区域，也有效克服了噪声的干扰，获得了稳定的区域提取结果，提高了最终结果的准确率。

另外，从表1和表2的结果来看，采用MRF模型检测目标，摆脱了复杂背景的干扰，比直接使用模板进行匹配的方法也获得了更好的性能。

本文的方法也能够被用在其他不同视角且具有复杂背景的异质光图像或同质光图像的目标检测问题中，只要参考图像和观测图像中包含能够被稳定提取的物体区域。

当然，本文仍然存在一些不足，主要就是在计算匹配区域的距离中，我们使用了最简单的互相关的方法。尽管该方法在实验数据集上获得了很好的匹配结果，但是我们仍然需要一个更加鲁棒的形状匹配算法。另外，本文是对地面物体区域进行配准，没有考虑高度信息无法忽略的三维目标。

我们的下一步工作是消除地面目标区域对结果的影响，将我们的方法完全扩展到三维目标的检测和匹配上，同时改进我们的区域匹配算法。

［1］Zitova B，Flusser B.Image registration methods：a survey［J］.Image and Vision Computing，2003，21：977－1000.

［2］Hild M，Umeda G.Image Registration in Stereo Based Multimodal Imaging Systems［C］／／In Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis.Los Alamitos：IEEE Computer Society，2005：70－75.

［3］马俊，曹治国.基于边缘信息的红外与可见光图像匹配技术［J］.计算机与数字工程，2006，34（12）：30－32.

［4］曾文峰.红外与可见光图像融合中的快速配准方法［J］.红外与激光工程，2002，31（2）：158－160.

［5］陶冰洁，王敬儒，张启衡.采用仿射变换的红外与可见光图像配准方法［J］.光电工程，2004，31（11）：39－41.

［6］Li H H，Zhou Y T.Automatic visual／IR image registration［J］.Optical Engineering，1996，35（2）：391－400.

［7］Li H，Manjunath B S，Mitra S K.A Contour Based Approach to Multisensor Image Registration［J］.IEEE Trans of Image Processing，1995，4（3）：320－334.

［8］Huang X S，Chen Z.A wavelet－based Multisensor image registration algorithm［C］／／In Proceedings of 6th international conference on Signal Processing.Los Alamitos：IEEE Computer Society，2002：773－776.

［9］Cheng H，Zheng S，Yu Q Z，et al.Matching of SAR Images and Optical Images Based on Edge Feature Extracted via SVM［C］／／In Proceedings of the 7th international Conference on Signal Processing.Los Alamitos：IEEE Computer Society，2004：930－933.

［10］Krotosky S J，Trivedi M M.Mutual information based registration of multimodal stereo videos for person tracking［J］.Computer Vision and Image Understanding，2007，106（2／3）：270－287.

［11］Matas J，Chum O，Urban M，et al.Robust widebaseline stereo from maximally stable extremal regions［J］.Image and Vision Computing，2004，22（10）：761－767.

［12］Fischler M A，Bolles R C.Random Sample Consensus：A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography［J］.Communications of the ACM，1981，24（6）：381－395.

［13］Huttenlocher D P，Klanderman G A，Rucklidge W J.Comparing Images Using the Hausdorff Distance［J］.IEEE Trans.On Pattern Analysis and Machine Intelligence，1993，15（9）：850－863.