基于改进遗传算法的微型电动车轮毂电机优化设计

陈齐平，舒红宇，任凯，陈里敏，陈博，谢安源

(1. 重庆大学 机械传动国家重点实验室，重庆，400044；2. 重庆神驰机电有限公司，重庆，400700)

随着世界经济的持续增长，石油资源紧缺和全球环境恶化问题受到各国政府和汽车企业的高度关注和重视，我国汽车行业提出可持续发展策略。实现汽车工业可持续发展的关键在于开发出节能环保电动汽车，其中包括发展用于短距离运输的微型节能电动汽车。由于永磁无刷直流电机具有功率密度较高、体积小、结构简单、起动转矩大、过载能力强、操作性好、可控性好、可靠性高、噪声低等一系列优点，因此，永磁无刷直流电机被广泛用作电动汽车的驱动轮毂电机。为了获得更高效率和更低成本的微型电动车轮毂电机，本文将优化设计出一款新型驱动轮毂电机。轮毂电机的优化设计过程是一个将工程设计问题转化为最优问题的过程，它是一个复杂的非线性、有约束、离散多变量的规划问题，采用传统优化算法，很难满足轮毂电机的全局最优解。近年来，遗传算法广泛应用于电机优化设计中。遗传算法(Genetic algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，它是由Holland于1975年首先提出的，通常被称为简单遗传算法[1]。简单遗传算法的主要优化设计步骤为：优化变量参数的选取、目标函数的确定、约束条件限制以及优化设计算法的选择[2]。针对驱动轮毂电机优化设计，Srinivas等[3]提出了交叉率和变异率能随适应度自动改变的自适应遗传算法；张明辉等[4]提出了一个依适应度调整交叉点和交叉率的自适应交叉算子，构造出合适的遗传算子，它是遗传算法能否成功使用的关键因素；Markovic等[5]进行了基于经典梯度法、直接搜索法和遗传算法的比较研究，得出遗传算法优化效果最优的结论；Upadhyay等[6]提出了用遗传算法优化设计永磁无刷直流电机的思路，指出优化的目标函数为效率、成本和温升，并取得了较好的优化效果。本文作者在对微型电动车轮毂电机进行研究的基础上，针对驱动轮毂电机设计特点，探讨了简单遗传算法和模式遗传算法在轮毂电机优化设计中的应用, 建立了驱动轮毂电机优化设计数学模型；针对它们优化设计效果不显著的缺点，提出一种改进的遗传算法，同时给出了简单遗传算法、模式遗传算法和改进遗传算法优化设计轮毂电机的算例，并对优化设计结果进行了对比分析。

1 理论与方法

微型电动车驱动轮毂电机的优化设计工作是在电机各项性能达到允许限度之内的同时，使电机的某些指标达到最优解，从而确定电机电磁系统的全部结构参数。常见的电机优化设计方法有简单遗传算法和模式搜索法。

1.1 简单遗传算法

轮毂电机的优化设计是一个具有不等式约束多离散变量的非线性规划问题。对于多目标函数的优化，可采用线性加权和的方法转为单目标函数,如式(1)所示，优化设计约束条件为式(2)所示，从而得出轮毂电机的数学模型，如式(3)所示[7-10]。

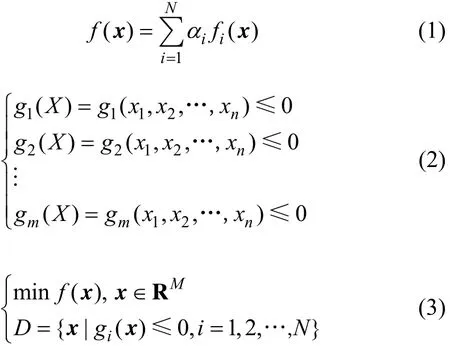
式中：f(x)为新的单目标函数；αi为N个权系数；fi(x)为第N个目标函数，x=[x1，x2，…，xn]T,为优化设计电磁参数；gm(X)为约束函数。

驱动轮毂电机的优化为有约束问题，而遗传算法一般应用于无约束优化，因此采用惩罚函数P(X，γ)将有约束问题转化为无约束问题[11-12]，如式(4)所示，其对应的增广适应度函数见式(5)。

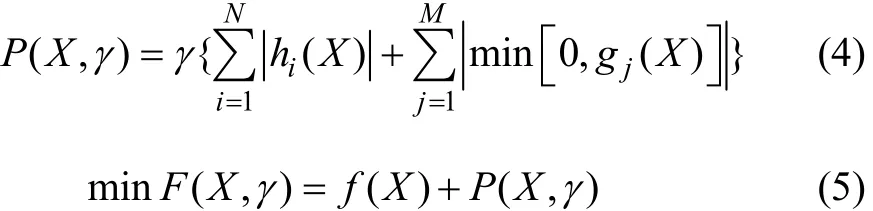
式中，γ为惩罚因素；hi(X)为等式部分函数；gj(X)为不等式部分函数。

1.2 模式搜索算法

模式搜索算法是直接优化方法，计算简便，不需要求解目标函数的倒数。它采用搜索点的局部测试信息来寻找目标函数的下降方向，采用探索移动和模式移动2种寻找方式，减少了迭代次数。探索移动沿着轴向探测有利方向，模式移动是沿着有利方向加速移动[13-14]。

设优化问题为求N元函数的最小值f(x)，具体优化过程如下。

步骤1 初始化，给定初始点x(1)，轴向方向为a1，a2，…，an，步长为λ，加速因子α≥1，缩减率β∈(0，1)，置y(1)=x(1)，k=1，i=1。

步骤4 如果f(y(N+1))＜f(y(k))，那么转入步骤5，否则，转入步骤6。

步骤6 如果λ≤ε，那么停止迭代，得x(k)，否则，

步骤7 置k=k+1，i=1，转入步骤2。

由于模式搜索法的优化效果与其所依赖的算法的初始解的收敛性密切相关，且对电机方案的优劣判断仅通过单个优化变量的数值增减而不是综合考虑多个优化变量数值的变化来决定，因此，模式搜索法难以实现全局最优解。若利用简单遗传算法，则得到初始解等，再应用模式搜索法，优化效果会更佳。

1.3 改进遗传算法

根据简单遗传算法优良的收敛效果和模式搜索法的收敛速度快的优点，提出了结合这2种算法的改进遗传算法。基本思想是采用自适应的交叉算子和变异算子的遗传算法对初始方案进行优化[15-17]，以此优化后的方案作为模式搜索法的初始方案进行快速收敛优化，从而得到效果最佳、效率最高的全局最优解。

对于求最小值问题，简单遗传算法的交叉算子Pc和变异算子Pv为：

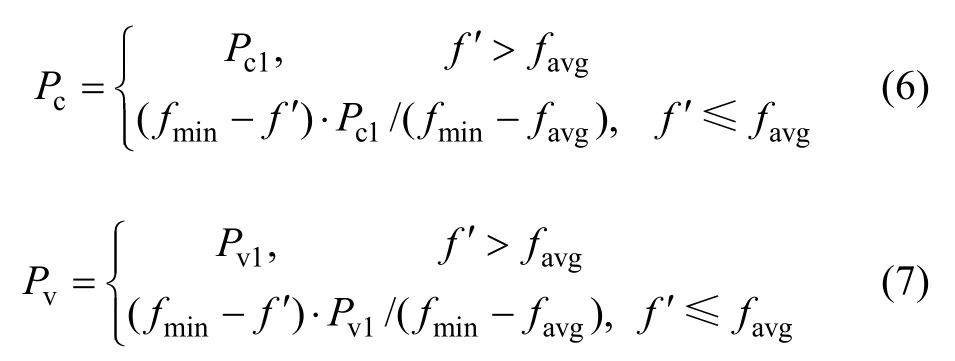
式中：Pc1和Pv1取(0，1)区间的值；fmin为群体中最小适应度；favg为每代群体中平均适应度；f′为要交叉的2个体较小适应度；f为要变异个体适应度。对于微型电动车驱动轮毂电机的有约束、多变量、非线性组合优化问题，由式(6)和(7)可知：遗传算子在进化初期搜索速度慢，在进化后期易使进化收敛于局部最优解，且进化代数与交叉率和变异率的取值无关。因此，必须改进自适应交叉率和变异率。

由于遗传算法的交叉率和变异率的精度和效率取决于种群个体的适应度。适应度较大时，为了保证减小基因遭到破坏概率，个体将采用较小的交叉率和变异率。适应度较小时，为了保证有利于扩大搜索区域，个体将采用较大的交叉率和变异率。因此，改进遗传算法的算子如下：

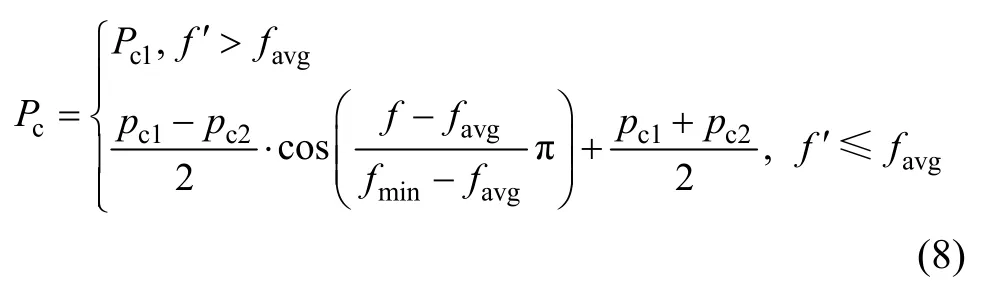
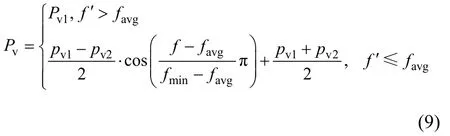
改进遗传算法在改进交叉率和变异率之后，就可嵌入模式搜索法的到位算子和最速下降算子，从而得到改进遗传算法的流程图，如图1所示。

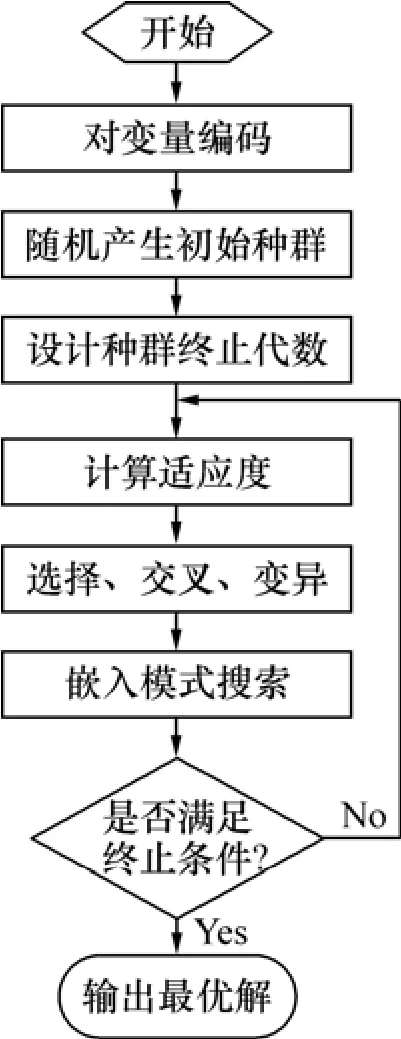
图1 改进遗传算法的优化设计流程图Fig.1 Flow chart of optimization design of improvement genetic algorithm

在微型电动车驱动轮毂电机优化设计时，优化变量参数的选取是一个核心环节，必须首先从变量参数对电机性能和成本、加工难易程度、结构布置和机辅程序的影响等几方面进行考虑，再综合考虑轮毂电机自身的设计特点，本文选取的优化设计变量为式(10)。

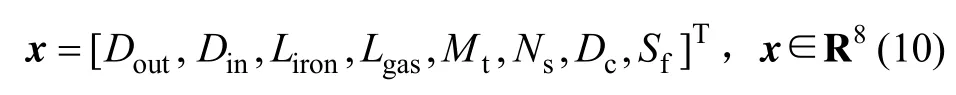
其中，Dout为定子外径；Din为定子内径；Liron为铁芯长度；Lgas为气隙长度；Mt为永磁体厚度；Ns为每槽导体数；Dc为导线直径；Sf为槽满率。

轮毂电机优化设计的约束条件主要包括边界约束和性能约束，本文的约束条件选择为启动电流Ist；启动扭矩Tst；气隙磁感应强度Bδ；额定转速NΓ；热负荷H；定子齿部磁密Bt；定子轭部磁密Bj；转子轭部磁密Bi。约束条件可表示为：

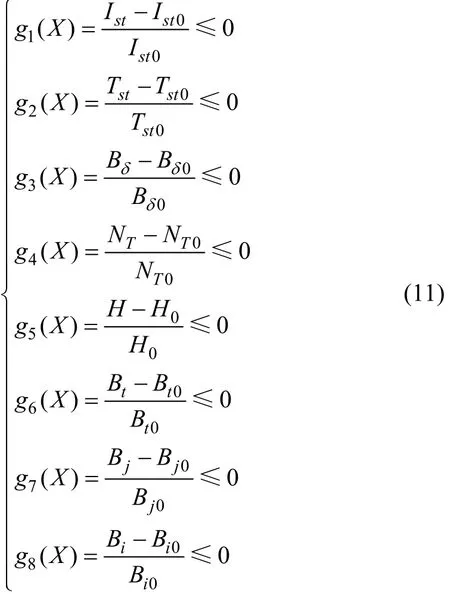
目标函数的选择是电机优化设计的一个重要的决策部分，它不仅体现了所研究问题的目的和性质，而且直接影响优化方案的理论价值和实用价值[18-19]。本文优化设计的目的是使轮毂电机的性能指标和经济技术指标最优化，因此，选取轮毂电机的有效材料质量、有效材料成本和电机效率作为目标函数。

2 算例分析

基于以上的理论和方法，对原机进行电磁设计，然后利用简单遗传算法、模式搜索算法和改进遗传算法对一台额定电压为36V，额定功率为250W，4极，15槽，双层绕组，Y型连接，内转子形式的微型电动车驱动轮毂电机进行优化设计。此轮毂电机的本体结构主要由带槽的定子、永磁体和转子构成；其工作原理是电枢绕组根据永磁磁极的位置信号确定导通状态，产生的反应磁场与永磁磁场相互作用，从而使轮毂电机产生稳定持续的电磁转矩。

优化目标函数主要为轮毂电机的有效材料质量、有效材料成本和电机效率，其表达式分别为：

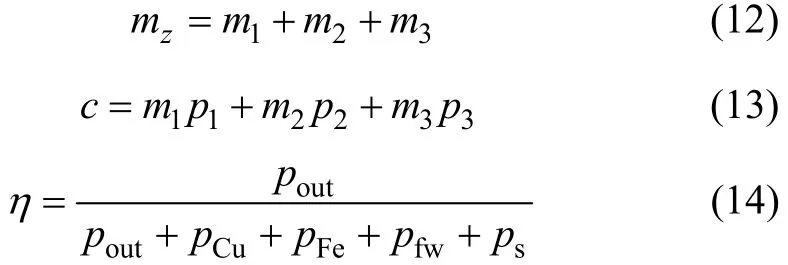
式中，mz为总质量；m1为永磁体质量；m2为铜线质量；m3为硅钢片质量；c为总成本；p1为永磁体单价；p2为铜线单价；p3为硅钢片单价；η为电机效率；pout为输出功率；pCu为铜线损耗；pFe为铁芯损耗；pfw为机械损耗；ps为杂散损耗。

约束条件除了满足加工工艺及给定额定值的要求之外，还需要满足启动电流，气隙磁密，定子齿磁密和转子轭磁密等要求。优化设计变量主要有定子外径，定子内径，气隙长度，永磁体厚度和每槽导体数等。

分别采用简单遗传算法、搜索模式算法和改进遗传算法对微型电动车驱动轮毂电机进行优化设计，优化前后各种参数如表1所示。在表1的基础上，得到初始方案与各种算法最优方案对比结果，如表2所示，其中铜价为56元/kg，硅钢片价格为7.7元/kg，永磁体价格为260元/kg。从表2可知：模式搜索算法的最高效率提高了 4.67%，简单遗传算法最高效率提高了6.68%，改进遗传算法最高效率提高了8.13%；模式搜索算法的材料成本降低了19.34%，简单遗传算法的材料成本降低了24.72%，改进遗传算法的材料成本降低了26.46%。改进遗传算法与模式搜索算法相比，最高效率提高 3.31%，且材料成本降低 9.68%；改进遗传算法相对简单遗传算法，最高效率提高 1.35%，且材料成本降低2.32%。

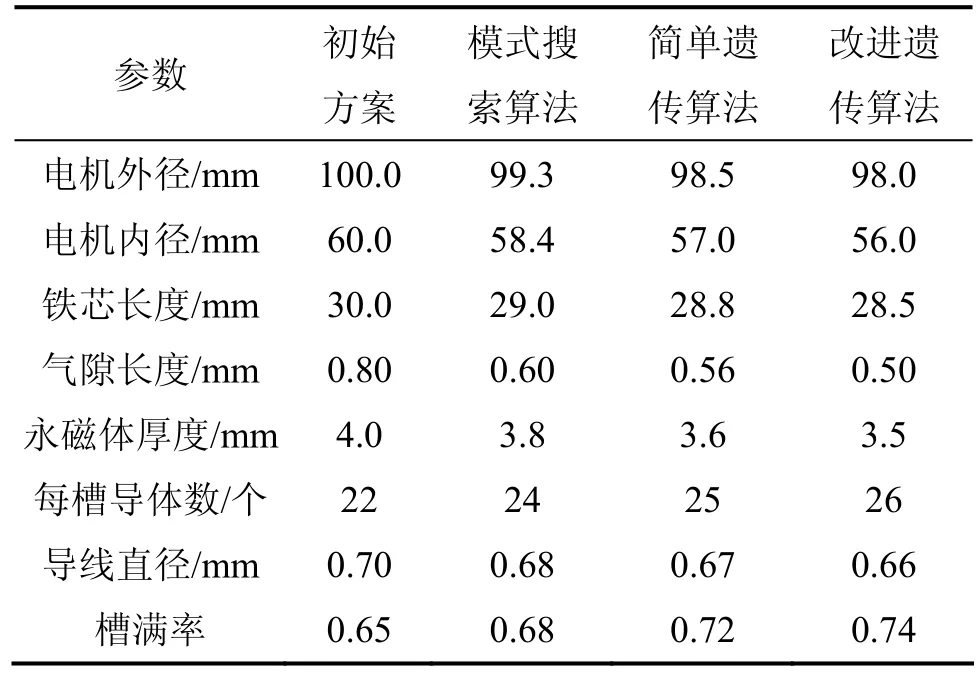
表1 优化前后各种参数变化情况Table 1 Changes of various parameters before and after optimization

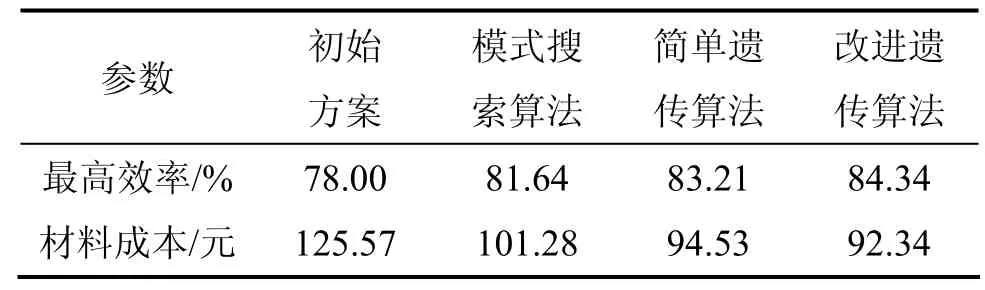
表2 初始方案和各种算法优化结果的比较Table 2 Results comparison of initial project and various algorithms optimization project

初始方案与各种算法的电机效率与转速的关系曲线变化图，如图2所示。

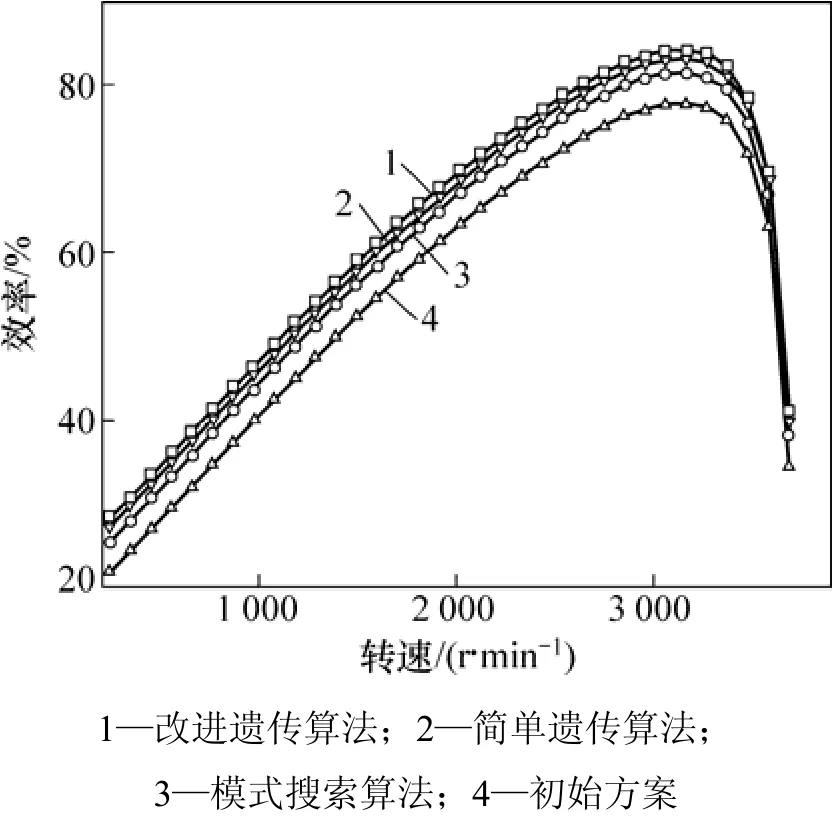
图2 优化前后电机效率与转速的关系Fig.2 Relationship between motor efficiency and speed before and after optimization

从以上分析结果可知，与简单遗传算法和模式搜索算法比较，本文提出的改进遗传算法相对较好，效率得到了提高，同时减轻了轮毂电机的质量以及降低了成本。

3 结论

(1)改进遗传算法和简单遗传算法优化效果均优于模式搜索算法，原因是在优化过程中，模式搜索算法局限于局部最优解，而遗传算法具有优秀的全局优化能力，得到的是全局最优解。

(2)改进遗传算法的优化效果比简单遗传算法有所提高，但提高幅度不大，原因是改进遗传算法是以模式搜索法为基础。然而，模式搜索法依赖于初始设计点的局部信息进行最佳搜索，只能收敛于初始点附近最优解；同时，改进遗传算法的求解迭代次数低于简单遗传算法的求解迭代次数，因此改进遗传算法的收敛速度更快，效率更高。

(3)改进遗传算法是一种具有全局收敛性和快速收敛性的现代优化算法，同时拥有优化效率高，优化效果好等特点，因此，将它应用于微型电动车轮毂电机优化设计是可行的，并且具有广阔的工程应用价值。

[1]Vasilija S, Lidija P, Milan C, et al. Comparison between two target functions for optimization of single phase shaded-pole motor using method of genetic algorithms[J]. Journal of Materials Processing Technology, 2005, 161(2): 89-95.

[2]Rahideh A, Korakianitis T, Ruiz P, et al. Optimal brushless DC motor design using genetic algorithms[J]. Journal of Magnetism and Magnetic Material, 2010, 322(22): 3680-3687.

[3]Srinivas M, Patnailk L M. Adaptive probabilities of crossover and mutations in GAs[J]. IEEE Trans on SMC, 1994, 24(4):656-666.

[4]张明辉, 王尚禁. 具有自适应交叉算子的遗传算法及其应用[J]. 机械工程学报, 2002, 38(1): 51-54.ZHANG Ming-hui, WANG Shang-jin. Adaptive genetic algorithm of crossover and its application[J]. Chinese Journal of Mechanical Engineering, 2002, 38(1): 51-54.

[5]Markovic M, Ragot P, Perriard Y. Design optimization of a BLDC motor: A comparative analysis[C]//Proceedings of the IEEE International Electric Machines and Drives Conference.Turkey, 2007: 1520-1523.

[6]Upadhyay P R, Rajagopal K R. Genetic algorithm based design optimization of a permanent magnet brushless DC motor[J].Journal of Applied Physics, 2005, 97(10): 516-525.

[7]陈金涛, 辜承林. 基于遗传算法的永磁直流电机优化设计[J].微电机, 2006, 39(8): 17-20.CHEN Jin-tao, GU Cheng-lin. Design optimization of permanent-magnet DC machine based on genetic algorithm[J].Micromotor, 2006, 39(8): 17-20.

[8]苏显方, 张著洪. 基于遗传算法的三环无刷直流电机控制系统研究[J]. 贵州大学学报: 自然科学版, 2009, 26(2): 74-77.SU Xian-fang, ZHANG Zhu-hong. Study on genetic algorithm-based three-loop brushless DC motor control systems[J]. Journal of Guizhou University: Science and Technology, 2009, 26(2): 74-77.

[9]舒红宇, 彭来, 谢鑫, 等. 基于遗传算法的电动代步车轮毂电机优化设计[J]. 云南大学学报: 自然科学版, 2011, 33(2): 1-6.SHU Hong-yu, PENG Lai, XIE Xin, et al. Design optimization of electric scooter hub motor based on genetic algorithm[J].Journal of Yunnan University: Science and Technology, 2011,33(2): 1-6.

[10]Vivier S, Gillon F, Brochet P. Optimization techniques derived from experimental design method and their application to the design of a brushless direct current motor[J]. IEEE Transactions on Magnetics, 2001, 37(5): 3622-3626.

[11]黄戡, 刘宝琛, 彭建国, 等. 基于遗传算法和神经网络的隧道围岩位移智能反分析[J]. 中南大学学报: 自然科学版, 2011,42(1): 213-219.HUANG Kan, LIU Bao-chen, PENG Jian-guo, et al. Intelligent back-analysis of tunnel surrounding rock displacement based on genetic algorithm and neural network[J]. Journal of Central South University: Science and Technology, 2011, 42(1):213-219.

[12]Jang S M, Cho H W, Choi S K. Design and analysis of a high-speed brushless DC motor for centrifugal compressor[J].IEEE Transactions on Magnetics, 2007, 43(6): 2573-2575.

[13]袁小芳, 王耀南, 吴亮红. 基于混沌变量的模式搜索法及其应用[J]. 湖南大学学报, 2007, 34(9): 30-33.YUAN Xiao-fang, WANG Yao-nan, WU Liang-hong. Pattern search algorithm using chaos and its application[J]. Journal of Hunan University, 2007, 34(9): 30-33.

[14]Al-Sumait J S, AL-Othman A K, Sykulski J K. Application of pattern search method to power system valve-point economic load dispatch[J]. Electrical Power and Energy Systems, 2007,29(10): 720-730.

[15]石山, 励庆孚, 王兴华. 基于自适应遗传算法的无刷直流电机的优化设计[J]. 西安交通大学学报, 2002, 36(12):1512-1518.SHI Shan, LI Qing-fu, WANG Xing-hua. Design optimization of brushless direct current motor based on adaptive genetic algorithm[J]. Journal of Xi’an Jiaotong University, 2002, 36(12):1512-1518.

[16]Janne K J. Comparison of nearest point algorithms by genetic algorithms[J]. Expert Systems with Applications, 2011, 38(8):10303-110311.

[17]Chung H P, Woo L, Woo S H, et al. Improved genetic algorithm for multidisciplinary optimization of composite laminates[J].Computers and Structures, 2008, 86(20): 1894-1903.

[18]康燕琴, 上官璇峰, 肖家乐. 圆筒型直线感应电机的遗传优化设计[J]. 机电工程, 2008, 25(8): 72-75.KANG Yan-qin, SHANGUAN Xuan-feng, XIAO Jia-le.Optimization design of tubular linear induction motor based on genetic algorithm[J]. Mechanical ＆ Electrical Engineering Magazine, 2008, 25(8): 72-75.

[19]梁昔明, 朱灿, 颜东煌. 基于物种选择的遗传算法求解约束非线性规划问题[J]. 中南大学学报: 自然科学版, 2009, 40(1):185-189.LIANG Xi-ming, ZHU Can, YANG Dong-huang. Novel genetic algorithm based on species selection for solving constrained non-linear programming problems[J]. Journal of Central South University: Science and Technology, 2009, 40(1): 185-189.