陆地高速移动环境下电波传播特性的建模与分析

张晓燕 闻映红 谈振辉

（1.北京交通大学电磁兼容实验室，北京100044；2.北京交通大学现代通信研究所，北京100044）

引 言

伴随着我国国民经济的迅速发展，尤其从“十一五”（2006年）起，我国的陆地高速轨道交通迎来了快速发展时期，地面交通正朝着高速度和高流量密度的趋势发展。已建成的线路的最高时速已达到或超过400km／h.为了使这些陆地高速交通工具在高速度、高流量密度的情况下实现安全行驶，目前普遍采用基于无线通信的控制方式。如目前高速铁路广泛使用的基于全球通信系统（GSM－R）的控制系统和城市轨道交通使用的基于局域网（WLAN）的控制系统。众所周知，复杂的电波传播信道是影响移动通信可靠性的主要因素，并且是研究移动通信系统组网设计、网络优化、资源分配以及信道编码、数据链路控制等方面的前提条件。因此，为了更好地促进高速铁路和其他高速陆地交通工具的安全快速发展，研究和预估在陆地高速移动环境下的电波传播特性刻不容缓。

现有的研究大都没有考虑高速轨道交通自身的特点，只是单纯地采用由车（汽车）载移动台得出的统计模型［1－3］分析高速铁路环境下的电波传播特性，虽然考虑了一些高速铁路的运行环境参数［4－6］，但仍与我国高速铁路的实际运行环境和状态有偏差，如高速铁路的场强覆盖区域是沿着线路的一个带形区域，而不是类似于公众通信的圆形覆盖；电波传播路径是一个在不断变化的有限状态的生灭过程，而不是一个单纯的马尔克夫过程等。因此，要建立与实际运行环境和状态更接近的仿真模型必须将高速铁路特有的地理环境、场强覆盖区域等环境参数和移动通信的运行状态参数等引入到仿真模型中。进而分析和研究高速铁路行驶过程中的电波传播特性。

1.基本理论

高速铁路自身的主要特点有：1）大部分时间内列车为直道行驶，铁路沿线地形的起伏坡度较缓，铺有较宽的路基，且沿线两侧设有隔离防护网；2）基站天线的场强覆盖范围为沿铁路线的带状区域；3）视距（LOS）路径在列车天线接收信号中占主要部分，基本可以认为接收的信号中至少存在一条LOS路径。如图1为典型的高速铁路运行环境和电波传播状态示意图。移动台接收的信号是各传播路径的叠加，那么研究电波传播特性归根结底就是研究电波传播各路径的特性。

图1 高速铁路运行环境示意图

根据以上高速铁路自身的特点，本文在文献［6］的基础上，通过引入有限状态的马尔克夫生灭链分析列车运行过程中电波路径的动态变化。

2.电波传播模型的建立

假设以高速列车为观测点，列车车顶天线与基站天线距离为dMB，基站天线高为hB＝40m，列车天线所在高度为hM＝3.97m.沿铁路线运行的列车，观察它在时间t内收到的电波径数，可以将这个过程看做为一个有限状态的生灭过程。

将时间区间［0，t］分成0，t1，t2，…，tn－1，t这n＋1个观察点，并且在每个观察点接收到的电波路径分别为 N0，N1，…，Nn－1，N.而且在ti后的任何时间tj，接收到的路径数目Nj最多与Ni有关，而与ti－1时刻以前的径数 N0，N1，…，Ni－1无关，其中i＜j，i＝1，2，…，n－1，且［ti，tj］和［tj，tk］内径数的变化ΔNij＝Nj－Ni与ΔNjk＝Nk－Nj独立，在t＝ti＋Δt时，观察到的径数变为N的概率只与Ni、N和Δt有关。由于在充分小的时间间隔Δt内，电波径数同时变化两条及以上的概率极小，在（t，t＋Δt］内变化一条路径的可能性与时刻t时接收到的径数N（t）有关，N（t）越大，再增加一条的概率越小，而减少一条的概率就越大；反之，N（t）越小，再减少一条的概率就越小，而增加一条的概率就越大。

设PNK表示接收机在时刻t时接收到的电波径数为N，经过Δt后接收到的径数变为K 的概率。接下来推导PNK（t，t＋Δt）.

由上述电波传播径数变化的特点，构造如下有限状态生灭链｛N（t），t≥0｝，表示时间间隔［0，t］内出现的电波径数。｛N（t），t≥0｝是一个有限非负整数状态集I＝｛Nmin，Nmin＋1，…，Nmax－1，Nmax｝，且时间连续的生灭过程。其中Nmin和Nmax分别为该有限生灭过程的最小和最大路径数。径数的状态转移过程如图2所示。

现在推导该有限生灭过程的转移概率PNK（t，t＋Δt）.

图2 电波径数状态转移图

式中，跃迁强度qNK为

式中：λ＞0表示电波径数增加一条的概率；μ＞0表示径数减少一条的概率，在本文中它们都为某段时间测量出的均值，因此，视为常数。

根据Chapman－Kolmogorov（C－K）方程，有

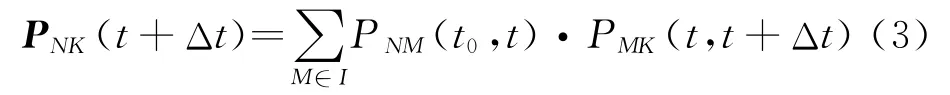
式中：t0≤t＜t＋Δt.将式（3）移项化简，并令Δt→0，可得PNK（t）的微分方程为

将式（4）应用到所有路径数目的转移概率就可组成电波路径转移概率矩阵微分方程，即

式中：

求解矩阵微分方程（5）可得任意数目的路径瞬时 转 移 概 率 PNM（t0，t）。该 微 分 方 程 可 以 利 用Kendall于1949年提出的母函数法来求解。

设G（u，t）为PNM（t0，t）的母函数，即

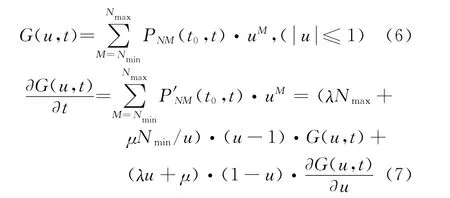
这是一个半线性微分方程，且其特征方程为

解特征方程（8），得出两个初积分：

式中：C1，C2是解微分方程得出的任意常数。为了确定 C1、C2，需 要 考 虑 初 始 条 件：PNM（t0，t）＝和将初始值代入式（9）和（10）得

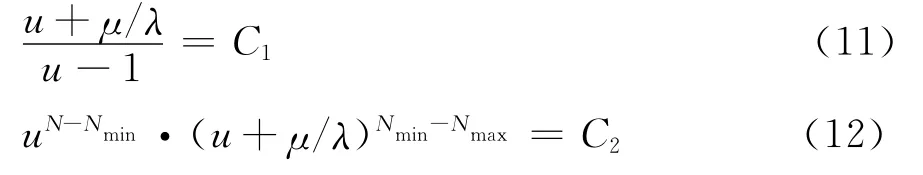
将u用C1表示有代入式（12）得将C1和C2分别用式（9）和（10）代替就可求出G（u，t），再结合式（6）求出PNM（t0，t）.

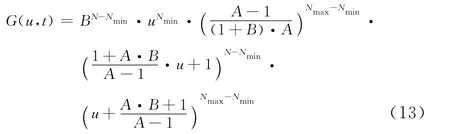
式中：A ＝e（λ＋μ）t，B ＝μ／λ.

求出

文献［6］中只是将路径变化看做是一个单纯的计数过程，因此，得出路径变化服从Poisson分布。引用该文献中关于高速铁路运行环境中地形地物等各个参数的定义，将运行环境与本文推导的电波路径转移概率相结合得出电波动态路径变化模型。

图3为Poisson分布和本文得出的分布两者的比较关系图，其中修正分布的结果由带星号曲线表示（图4也是）。图3的仿真环境为：较平坦地形上（地形地物占有系数C＝0.2，地形高度差H＝40m，地形起伏系数g＝0.3），dMB＝300m，带状小区覆盖长度d＝3km，运行速度v＝300～500 km／h，载 频fc＝900MHz，λ ＝ 0.5v，μ ＝为路径数目的平均值）。

为了能更清楚地看到两者的差别，现将其中一接收点的数据抽出为图4.

由图3和图4可以看出在此运行环境下，如果接收路径数目较小时，两者的差别较大，随着接收路径数目的增大，两者趋于一致；且Poisson模型的平均路径数稳定在1～2条，本文模型的平均路径数随着位置的不同平均路径数也不同，但基本上都是大于2条，这与实际运行环境所测得的路径数目较接近。即接收的路径至少包括LOS、一条通过大地或列车车顶等位置反射的路径和可能一条甚至更多其他反散射物体反散射的可分辨路径（大部分这些路径经过多次的反散射到达接收天线处的功率已低于接收门限，因此可忽略）。

图3 在不同观测点处得出的Poisson和本文推出的分布

造成这种差别的主要原因是：Poisson分布是由单纯的计数过程得出，并没有考虑前后两次计数之间由实际物理过程造成的联系。

根据广义平稳非相关散射（WSSUS）模型可知接收天线接收到的信号可表示为

式中：E（t）为本地中值电平，服从对数正态分布；S（t）为调制信号；a0为LOS路径的衰减系数（为复数）；ai为第i条路径的衰减系数（包含了信号从发射到接收所经历的所有变化，均为复数，即有幅度和相位信息）；fd0为视距路径的多普勒频移；fdi为第i条路径的多普勒频移fdi＝fdmaxcos（θi），其中fdmax＝vfc／c，θi为第i条接收路径与机车运动方向的夹角，在0～π／2内按高斯分布随机取值［6］，c是光速；τi为相对于发射信号，第i条路径的延时，假设其服从0～τmax内的均匀分布，τmax为该接收点所能接收的最大延时；N为某时刻所接收到的电波路径数。

有了上述的动态接收路径转移概率，通过建模每条路径的衰减系数来模拟该路径的传播过程，除了LOS路径外，其他的路径衰减系数均包含了自由空间的传播损耗和多次反散射引起的电波能量损失，如果该段路径中存在绕射，则该路径可以忽略［7］。

第i条路径传播过程中所经历的反散射次数Ni服从如下Poisson分布［6］

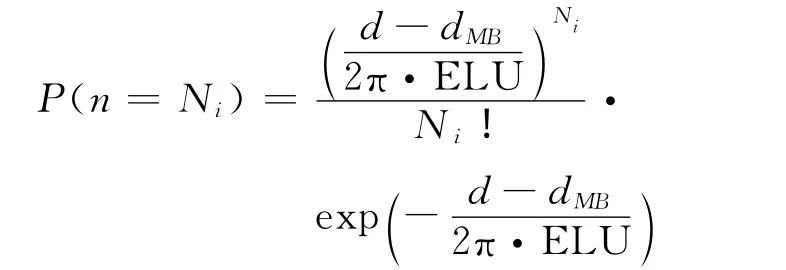
式中：ELU为平均地形起伏长度，ELU＝H／g.假设第i条路径中每段相对衰减系数为ai，j，其中j＝1，…，N，则该路径的衰减系数为ai＝ai，1ai，2，…，ai，N.

第i条路径上，各段反散射的路程Li，j服从指数分布［6］

则每段反散射的相对衰减系数有如下关系

式中：Γi，j为每段的相对反射系数。由于接收天线通常都是垂直安装的单极天线，接收天线主要是接收多径电波中的垂直极化分量，则反射系数为

式中：εi，j、ε′i，j分别为每个反射点和入射点的介电常数（无线通信中，常见材料的介电常数见文献［7］的第55页，铁路通信环境中还有很多金属，如机车车顶、基站天线塔等反射体），θi，j为每段的入射角。

第i条路径的总路程Li服从如下分布式（17）［6］，如图5所示。

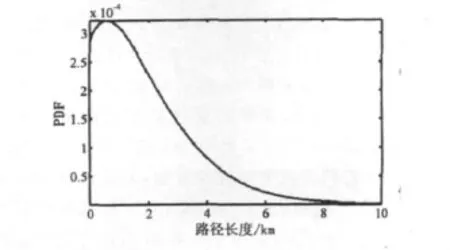
图5 第i条路径的路程Li的概率密度分布

在仿真中需要将Li，j和Li联系起来：如通过式（17），确定了一段总路程Li，那么由式（16）得出的各段Li，j之和应等于Li.除此之外，假设基站发射功率为20W，接收门限为－95dBm［8］.

3.仿真结果与讨论

3.1 仿真结果与分析

由上述分析，且为了简便暂时不考虑调制信号信息。300km／h时的仿真结果如图6所示。

从图6（a）和（b）可以看出接收路径数目在不同的观察时间的变化为1→2→2→2→2…→2→2，衰减系数的变化范围为0～138dB（与发射信号归一化后），延时时间最大可以达到111ms.而平均延时小于3.2μs，均方延时扩展低于2.12μs.从图6（d）可以看出多普勒频谱的最大值出现在－200.5Hz，加上铁路通信的自身特点，由该值可以得出电波传播的方向与列车的运动方向一致，列车远离发射源，且LOS传播方向与列车的运动方向间的夹角为θ≈36.7°，列车到基站的水平距离约为405m.

500km／h时的仿真结果如图7.

对照300km／h的仿真结果，可以得出500km／h时的类似结果：由如图7（a）和（b）可得其接收路径数目变化过程为：1→2→2→1→2…→2→2，衰减深度仍可达到138dB，最大延时时间为53ms，平均延时低于1.8μs，均方延时扩展小于1.36μs，而且对比图6（c）和图7（c）可以发现随着速度的增加，接收信号的幅度衰减趋于剧烈，相位的变化呈加快趋势。从图7（d）可以看出多普勒频谱的最大值位于386.7Hz，即列车的运行方向为靠近发射源，电波传播方向与列车运动方向间的夹角θ≈22°，列车到基站的水平距离约为751.9m.综合图6和图7，还可以确定仿真环境下的最大码元周期Rb（Rb＜1／στ）和相关带宽Bc＝1／（2πστ）等。

3.2 模型有效性检验

多次运行仿真程序得出了20 000个数据（速度为300km／h），对这些数据进行统计，结果如图8所示。从数据拟合的曲线可以看出其斜率为－2.452×10－7≈0，且常数项为0.002 778≈1／360，可以说本模型接收信号的相位分布符合均匀分布。

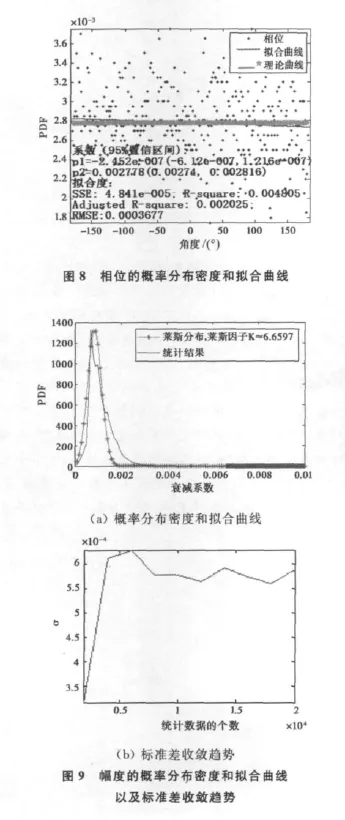
从图9可以看出：幅度衰减系数的标准差在统计数据超过8 000个后基本趋于稳定。统计得出的幅度概率密度分布近似服从莱斯概率密度分布，莱斯因子K≈6.659 7.统计得出300km／h时的电平通过率为113.986Hz，500km／h的电平通过率为197.896 5Hz，也就是说，随着速度的增加电平通过率会增加，衰落速度也会变快。

4.结 论

通过对电波路径有限生灭过程的推导得出电波路径的转移概率，将它与实际陆地高速移动电波传播环境相结合建立起更符合实际运行环境的电波传播模型。通过该模型研究了较平坦地形下的高速铁路电波传播特性，证实了模型的有效性。此外，研究更为详细的、更贴近高速铁路电波传播运行环境（比如将天线的参数、铁路特有设施、调制信号信息等的影响加入模型）的模型以及传播特性对通信性能的影响等都将是接下来要继续的工作内容。

［1］PATZOLD M.Mobile Fading Channels［M］.New Work：John Wiley ＆ Sons，Ltd.，2002.

［2］GARCIA C R，LEHNER A，STRANG T，et al.Channel model for train to train communication using the 400MHz band［C］／／VTC Spring 2008－IEEE Vehicular Technology Conference，2008：3082－3086.

［3］WIESBECK W and KNORZER S.Characterist－ics of the mobile channel for high velocit－ies［C］／／International Conference on Electromagnetic in Advanced Applicat－ions，2007：116－120.

［4］NAKAMURA K，KAWASAKI K，SHINDO M.Development of methods for the calculation of radio propagation characteristics in the railway environment［J］.Quarterly Report of the Railway Technical Research Institute，2002 43（4）：182－186.

［5］HATTORI T and ABE K.Analyses of propagation characteristics in future railway communication systems using 25GHz band radio［C］／／IEEE 49th Vehicular Technology Conference，2000：2288－2292.

［6］赵庆安.在高速铁路环境下电波传播特性的模型分析［D］.北京：中国铁道科学研究院，2000.

［7］BERTONI H L.Radio Propagation for Modern Wireless Systems［M］.Pearson Educa－tion，Inc.，2000.

［8］王惠生，马良德，高利民.铁路客运专线GSM－R基站覆盖的探讨［J］.中国铁路，2009，39（7）：57－60.WANG Huisheng，MA Liangde，GAO limin.Discussion on GSM－R center covering of PDLs［J］.Chinese Railways，2009，39（7）：57－60.（in Chinese）