传导冷却电流引线热分析

昌 锟 赵保志 雷沅忠 谢秀娟

1 引言

电流引线是超导磁体系统中连接室温电源和超导磁体的关键通流部件。电流引线常常是超导磁体系统的主要漏热源，在大型超导磁体系统中，电流引线漏热占磁体总漏热的比例甚至达到50%［1］。为保证超导磁体系统稳定运行，需尽量减小通过电流引线向磁体的漏热，本文拟通过对传导冷却电流引线进行热分析计算，研究减小漏热的电流引线优化途径。

2 电流引线传热模型

电流引线轴向温度梯度远大于径向温度梯度，对于传导冷却电流引线可忽略辐射漏热和残余气体分子导热的影响［2］，则热传递只与引线长度方向相关，进而可采用一维传热模型来进行分析。

电流引线可由常规材料(铜或铜合金)制作，也可采用常规材料与高温超导材料分段制成组合引线，但传热分析计算均可用一维理论来分析，具体计算时可采用分段方法进行分析计算，只需对各段边界条件进行调整。典型的传导冷却电流引线可由制冷机冷却［3-4］，其一维传热模型可参见图1所示。为便于分析，现取铜引线部分进行传热分析(见图2)。

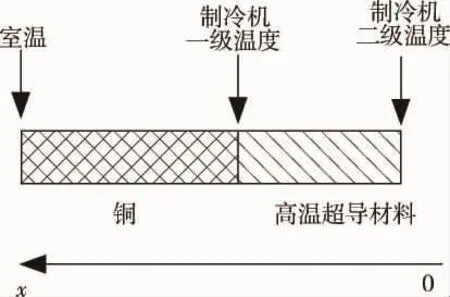
图1 电流引线传热模型Fig.1 Heat transfer model of current lead

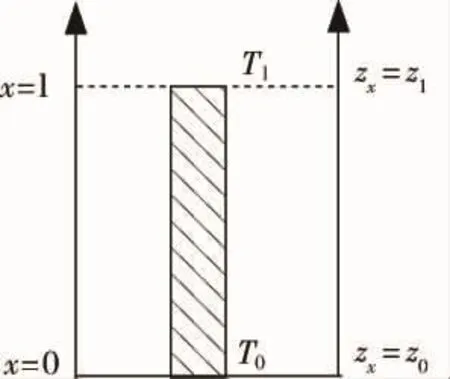
图2 铜引线部分示意图Fig.2 Schematic diagram of copper current lead

依据一维传热模型可得热平衡方程:

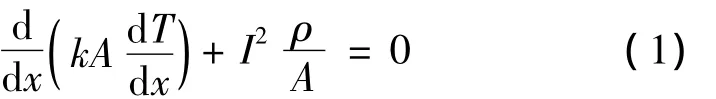
式中:ρ为电阻率Ω·m;k为热导率，W/m·K;A为电流引线截面积，m2;T为温度，K;I为流过电流引线的电流强度，A。为解此方程，作如下变换:

代入式(1)中得:

假定材料的热导率和电阻率符合威德曼—弗朗兹(Wiedemann-Franz)定律，即材料的热导率和电阻率互为倒数:ρk=L0T，L0=2.45×10-8W·Ω/K2称为洛仑兹常数［5］。则式(3)可得:

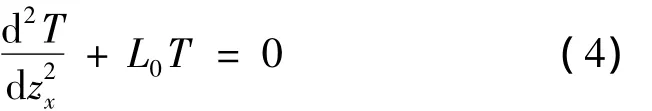
通过求解式(4)可得电流引线上的温度分布关系式及引线两端的传热关系式。

(1)温度分布

式(4)中的特征方程为:r2+L0=0

则方程的解为:

如图2所示，设定铜引线的长度为l，对应长度l处的温度用Tl表示，其对应的边界条件为:

代入方程中可得:

则引线上温度分布为:

(2)传热量

引线上的传热量可由式(7)计算

将所得的温度分布关系式(6)代入得:

则对引线底部zx=z0=0有:

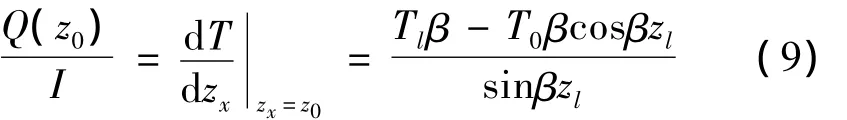
对引线的上部，zx=zl有:

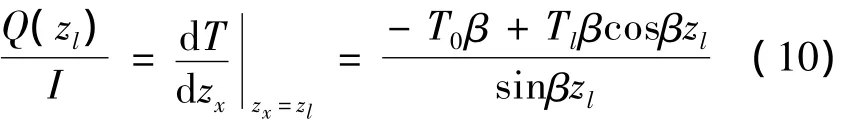
3 电流引线优化

对电流引线进行优化设计是减小外界向磁体漏热的有效途径。如图2所示，引线底部(x=0，或zx=z0=0)对应的传热量即为向磁体流入的热量。对电流引线进行优化，要求从引线流入磁体方向的热量最小，即要求Q(z0)取最小值，由式(9)得电流引线的优化参数zl满足如下关系:

将式(9)代入式(11)得:

则可得:

由式(12)对应的可得:

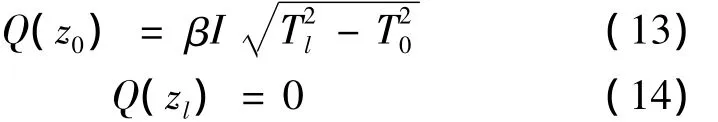
若其它条件已知，由式(12)可导出zl的优化值，进一步利用式(2)可得到电流引线结构尺寸的参数关系。式(13)和式(14)表明，当电流引线温度较低端的漏热最小时，电流引线温度较高端无热量传递，此处不存在温度梯度。

4 电流引线漏热分析

4.1 zl取最佳值

由上可知优化参数zl包含了电流引线的材料热导率，通电电流，引线的长度及截面积因素，现将其作为综合参数进行分析。

当zl均取最佳值时，由式(13)所示最小传热量中可得，电流引线温度较低端的传热量与电流引线两端的温度及通过的电流相关。当通电电流不同时，作为实例，取T0=80 K，通电电流分别为 I=50，100，200 A，Q(z0)随 Tl的变化规律见图3所示。

图中曲线表明:

(1)除Tl与T0接近区域，随着Tl降低，Q(z0)也降低，且Q(z0)与Tl基本呈线性关系，表明降低Tl可降低电流引线低温端的换热Q(z0)。

图3 通电电流不同时Q(z0)与Tl的关系Fig.3 Relation of Q(z0)and Tl for different current

(2)Tl相同时，电流引线通过的电流越大，引线温度较低端的换热Q(z0)越大，且Q(z0)随Tl的变化越大。表明电流越大，通过降低Tl可以更显著的降低电流引线低温端的换热量。

当T0不同时，设定通电电流为I=100 A，分别取T0=40，60，80 K，Q(z0)随 Tl的变化规律见图4 所示。

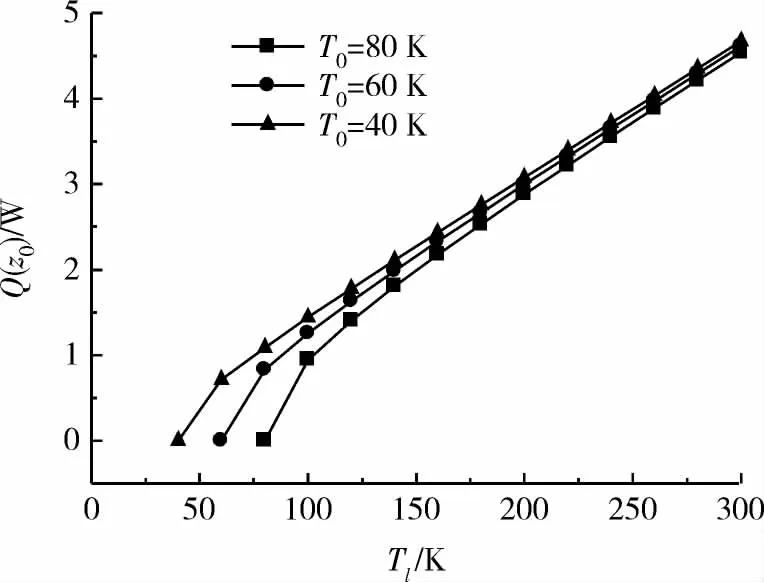
图4 T0不同时Q(z0)与Tl的关系Fig.4 Relation of Q(z0)and Tl for different T0

据图中曲线可得:除Tl与T0接近的情况，Q(z0)随Tl降低而降低，且Q(z0)与Tl基本呈线性关系。相同条件下，T0越低，Q(z0)越大，即引线温度较低端的漏热量越大。T0越高，曲线的斜率越大，表明电流引线温度较低端的温度越高，降低Tl可更显著的降低电流引线低温端的换热量。

4.2 zl偏离最佳值

当电流引线参数zl偏离最佳时，相应Q(z0)将增大，下面通过实例分析zl偏离最佳值时，对应Q(z0)的变化特点。

设定 Tl=300 K，T0=80 K，I=100 A，则对应漏热最小时zl的优化值可由式(12)导得zl=8 285.755 A·K/W。若将zl分别以10%递增和递减(以z'l表示)，则漏热增大，由式(9)可得Q(z0)，相应变化曲线见图5所示。

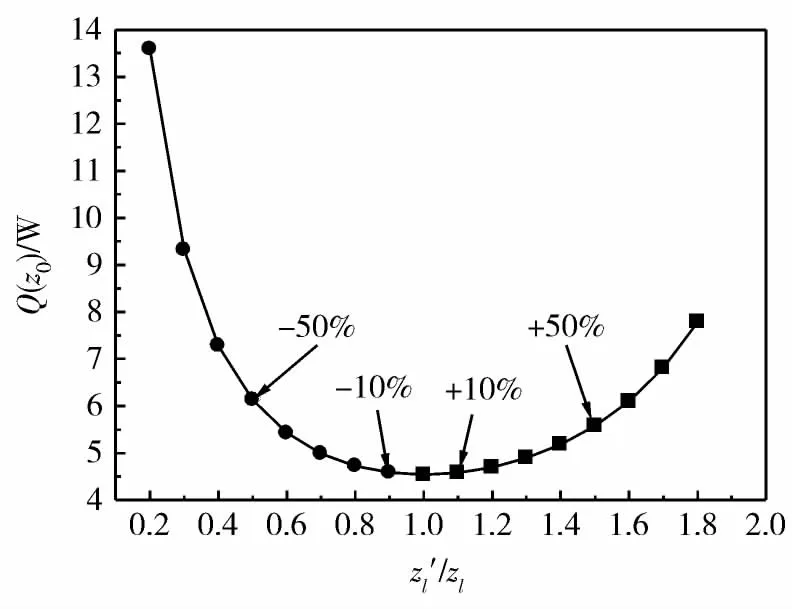
图5 zl偏离最佳时，Q(z0)的变化情况Fig.5 Variation of Q(z0)with z'l/zl

由图可得:

(1)zl增加和减小相同百分比，zl减小时对应的Q(z0)值大于zl增加时对应的Q(z0)值，且zl同时增加和减小的数值越大，对应的Q(z0)相差越大，表明增加zl比减小zl更有利于降低通过电流引线的漏热量。

(2)当zl偏差较小，如本实例中增加或减小10%时，对应Q(z0)变化很小，几乎可以忽略不计。当偏差较大时，对应Q(z0)差别较明显，依据图中数据有:当zl取最佳值时，即z'l/zl=1，对应Q(z0)=4.54 W，当zl增加50%时，对应Q(z0)=5.57 W，换热量增加22.7%，而当zl减小 50%时，对应 Q(z0)=6.13 W，换热量增加35%，两者相差12.3%。因此对于实际的电流引线，当zl不能取最优值时，应尽可能增加而不是减小zl。

5 结论

通过对传导冷却电流引线的传热分析，获得了电流引线最小漏热对应的优化关系式。通过实例分析了优化参数zl取最佳值时，电流引线两端温度及电流与漏热的关系，结果表明:降低电流引线温度较高端的温度，可以有效减小电流引线漏热;当电流引线的优化参数zl偏离最佳值时，增加zl比减小zl更有利于降低通过电流引线的传热量。

1 康志成.大型超导磁体电流引线理论及应用［M］.北京:国防工业出版社，2009，14-15.

2 范宇峰，龚领会，张 亮，等.制冷机直接冷却高温超导磁体电流引线优化设计［J］.低温工程，2005(5):17-21.

3 石 零.低温真空电流引线热分析［J］.低温工程，2005(4):53-55.

4 Ho-Myung Chang，Yeon SukChoi，Steven W Van Sciver.Optimization of operating temperature in cryocooled HTS magnets for compactness and efficiency［J］.Cryogenics，2002，42(12):787-794.

5 康志成，丁立人，翁佩德.超导磁体气冷电流引线的优化设计［J］.核科学与工程，2003，23(4):348-352.