有耗介质中时域精细积分方法的数值色散分析

孙 刚 马西奎 白仲明

（西安交通大学，电气工程学院，电力设备电气绝缘国家重点实验室，陕西 西安710049）

引 言

时域有限差分（FDTD）方法［1－2］是一种有效的电磁场时域计算方法，并已广泛应用于电磁散射、电磁兼容、波导与谐振腔系统、天线辐射特性的研究［3－6］。然而，FDTD的空间步长要受到数值色散条件的限制，其时间步长要受到柯朗（Courant）稳定性条件的限制。一般而言，空间步长要小于电磁波波长的1／10［2，7］。这些限制条件使得应用 FDTD分析电大尺寸（仿真模型的几何尺寸远大于电磁波的波长）问题时所需求的计算机CPU时间和内存过大，出现计算困难。

为了克服FDTD的上述固有缺陷，文献［8］提出了交替方向隐式时域有限差分（ADI－FDTD）方法。ADI－FDTD是无条件稳定的，但是数值色散误差较大。文献［9］的研究表明：当电导率较大时，ADI－FDTD的应用要受到限制。

为了解决FDTD和ADI－FDTD的上述问题，时域精细积分（PITD）方法［10］将精细积分技术［11］引入到时域电磁场计算之中。PITD的时间步长可以远大于Courant条件所限制的值［12］。在无耗介质中，PITD的数值色散误差略大于FDTD的数值色散误差，小于ADI－FDTD的数值色散误差，且基本上不受时间步长的影响［13］。

文献［13］对PITD的数值色散分析仅限于无耗介质。分析有耗介质中PITD的数值损耗和数值色散，将为其在有耗介质中的应用和进一步发展提供理论基础。

1.数值色散方程

1.1 时域精细积分方法的基本原理

在PITD中，首先应用Yee网格对两个麦克斯韦（Maxwell）旋度方程

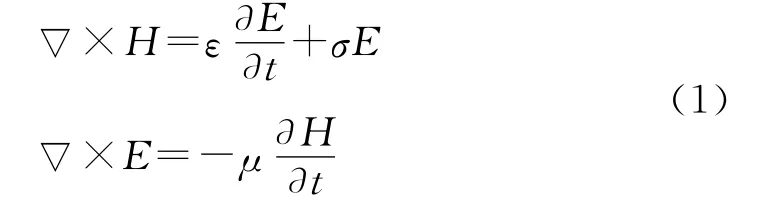
进行空间离散，得到如下的常微分方程组［10］：

式中：X＝ ［Ex，Ey，Ez，Hx，Hy，Hz］T是由网格结点上的电场分量和磁场分量构成的列向量，M是一个由空间步长（Δx，Δy，Δz）决定的系数矩阵。若引入空间位移算子Xh，Yh和Zh［14］，就可以将 M 矩阵表示成如下的形式

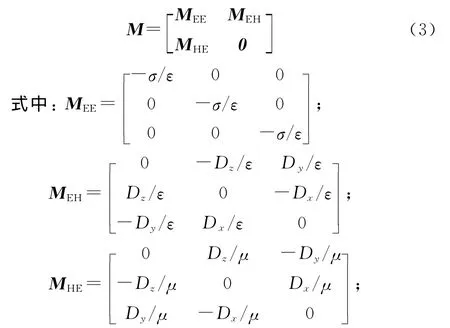
Dx＝和是空间差分算子。

根据常微分方程组理论，可以得到X的时间递进公式

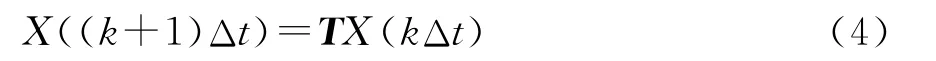
式中：Δt是时间步长；T＝exp（Δt M）.

指数矩阵T的高效率、高精度计算是式（4）递进计算的关键。在PITD中，采用如下的有限项泰勒级数展开对T进行精细积分计算［11］

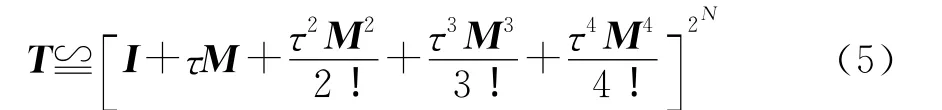
式中：τ＝Δt／2N是子时间步长，N是预先选定的整数，一般取N≥20.有关应用精细积分技术计算式（5）的详细过程见文献［10］［11］。

1.2 一维数值色散方程

在一维情况下（X＝ ［Ex，Hy］T），矩阵M 就简化成

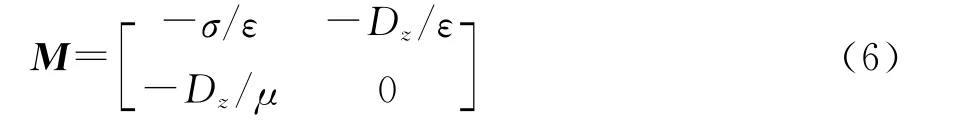
对于沿着z方向传播的正弦均匀平面波，X在时间－空间谱域内，可以表示成如下的离散形式［2］

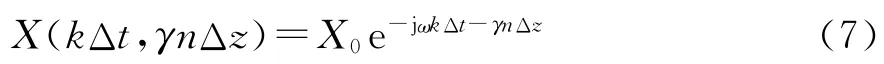
其中：γ是数值传播常数。此时有

不难看出：矩阵M的特征值λM要满足如下的方程

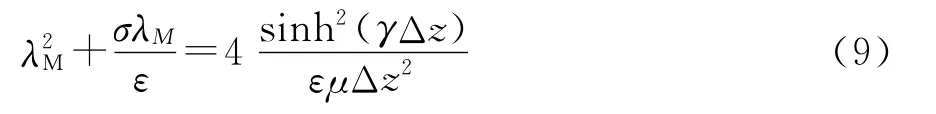
注意到矩阵M是可对角化的

式中，Y是由矩阵M的特征向量构成的矩阵。将式（10）代入式（5），有

即矩阵T也是可对角化的，并且有

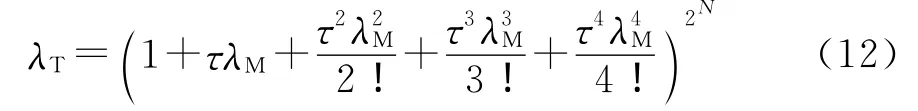
式中，λT是矩阵T的特征值。将式（7）代入式（4），就可以得到

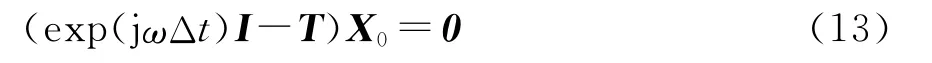
上述方程的非平凡解要求

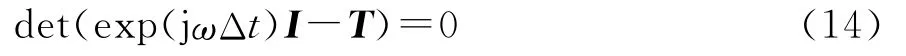
利用式（11）和式（12），可以将式（14）简化成

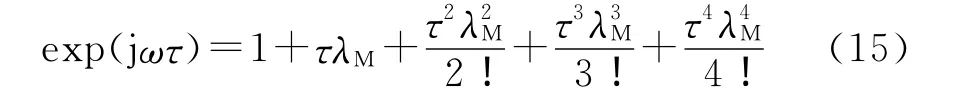
在 PITD 中，τ 是 一 个 很 小 的 量［10－11］，因 此，式（15）的右边可以近似表示成

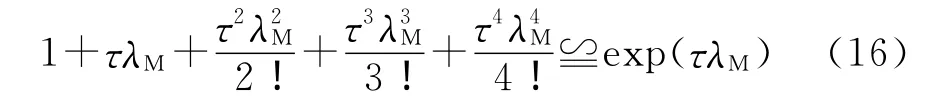
比较式（15）和式（16），不难看出：λM≌jω.不妨设λM＝jη，此时式（15）可以表示成

将γ＝α＋jβ（α是数值衰减常数，β是数值相位常数）代入式（9）就可以得到

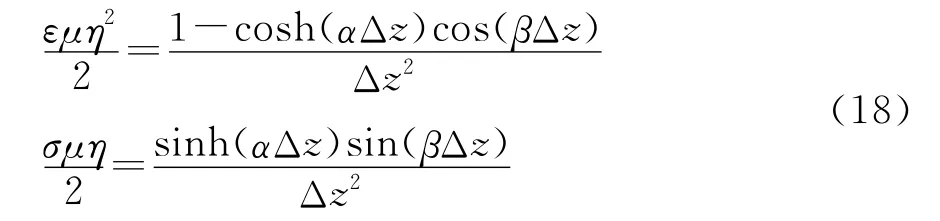
式（17）和式（18）共同构成了一维情况下有耗介质中PITD的数值色散方程。

1.3 三维数值色散方程

在三维情况下，PITD的数值色散方程可以由一维情况直接拓展得到，不再赘述其推导过程，只给出其结果如下

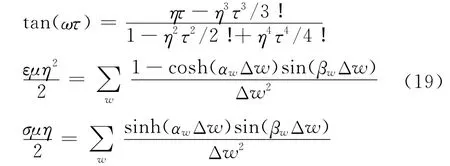
式中：w＝x，y，z.并且有

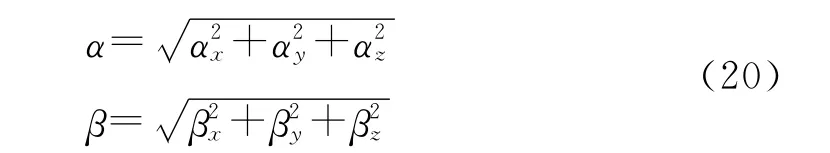
在式（19）中：α和β是通过三角函数和双曲函数耦合的，这些函数的变量中还包括了电磁波的传播方向。因此，无法直接计算α和β.α和β的值，但可以应用Newton－Rahphson方法迭代得到。

为了研究数值损耗和数值色散的各向异性，通常要考虑数值波沿坐标轴方向（可以等效为一维情况）和数值网格对角线方向的传播特性。在一维情况、二维正方形网格情况（Δx＝Δy＝Δ）和三维正立方体网格情况（Δx＝Δy＝Δz＝Δ）下，式（19）可以简化如下

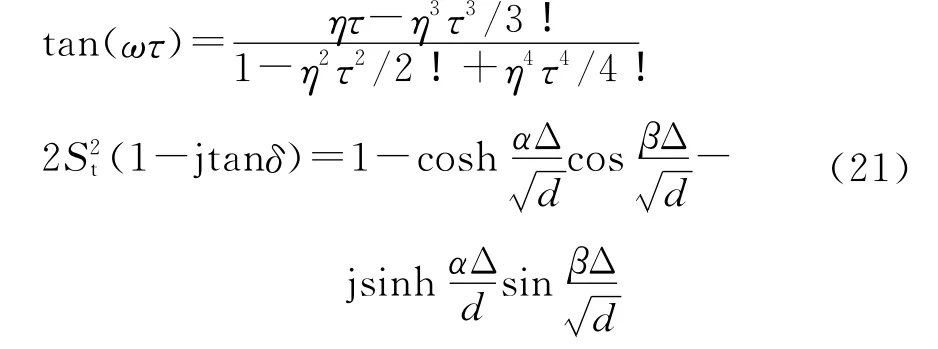
式中：tanδ＝（ω／η）tanδ0是数值损耗角正切，tanδ0是损耗角正切表示空间维数。由η≌ω可知：tanδ≌tanδ0，即PITD的数值损耗角正切是损耗角正切的高精度近似。式（21）中的α和β是可以进一步分离的，有

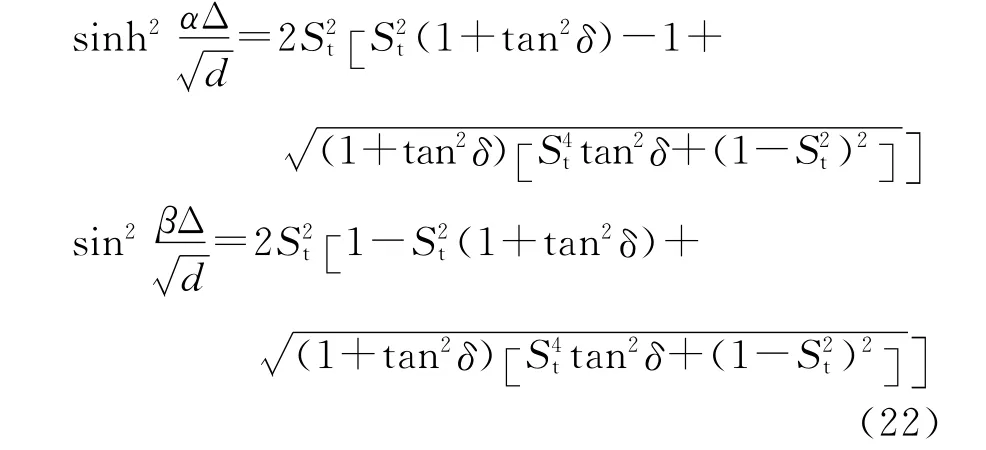
式（22）可以用于直接求解数值波沿坐标轴方向和对角线方向传播情况下的α和β.

对比式（19）和有耗介质中FDTD的数值色散方程式（23）［15］，

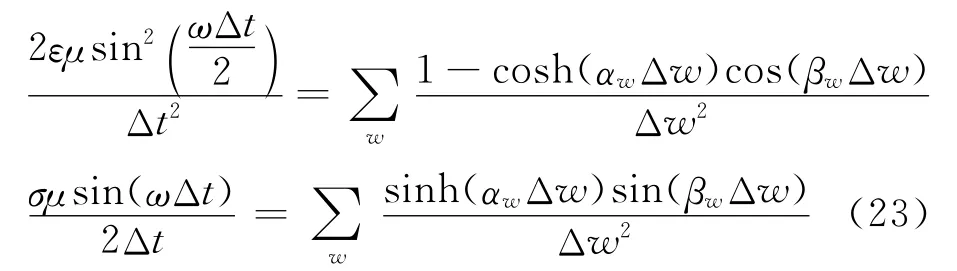
可以看出：当时间步长趋近于0时，式（19）和式（23）将趋于一致。这是因为这两种方法在空间上都采用了Yee网格离散。当时间步长趋近于0时，数值色散方程体现出的就是空间离散网格的数值色散特性。

当电导率σ趋近于0时，式（19）将变为无耗介质中PITD的数值色散方程［13］

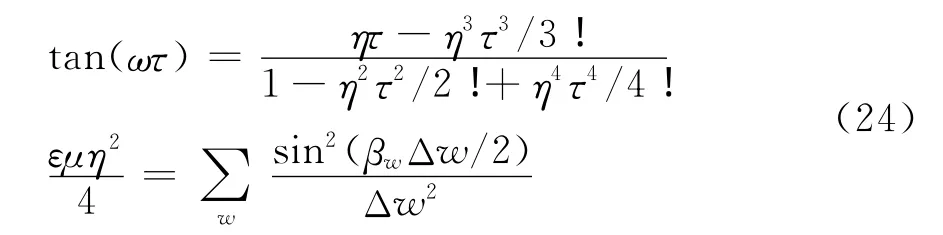
当空间步长和时间步长均趋近于0时，式（19）将趋近于有耗介质中电磁波传播的色散方程

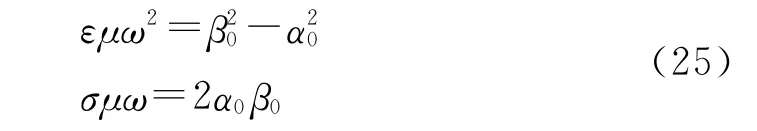
式中：α0是电磁波的真实衰减常数；β0是电磁波的真实波数。

2.数值损耗和数值色散分析

首先分析在一维情况下（电磁波沿x方向传播，ε＝ε0，μ＝μ0），时间步长 Δt、空间步长 Δx 和电导率σ对PITD的数值损耗和数值色散的影响。然后分析在高维情况下，PITD的数值损耗和数值色散的各向异性。定义数值损耗误差（NLE）和数值相位误差（NPE）分别如下

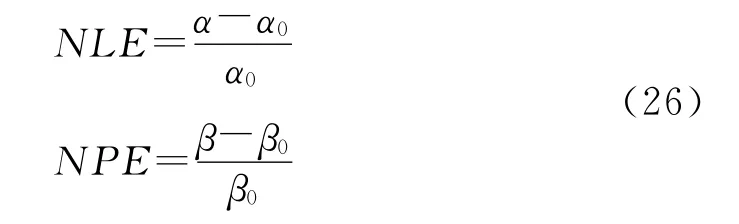
2.1 时间步长的影响

在一维情况下，PITD的NLE和NPE随时间步长的变化如图1所示。电磁波频率f＝300 MHz，空间采样密度（电磁波波长／空间步长）Nλ＝20，Courant常数S＝cΔt／Δx∈（0，1024），预先选定的整数N＝20，电导率σ分别等于3E－4S／m，3E－2S／m和30S／m（通常电介质材料的电导率σ∈（1E－4，30）S／m）.

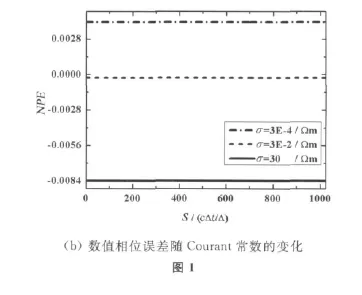
在图1中，所有的曲线都几乎是平直的。这说明PITD的数值损耗和数值色散都基本上不受时间步长的影响。其原因是PITD的数值色散方程式（19）中所包含的时间量（子时间步长τ）被限制在很小的范围内（τ≤2.722E－13s）.

2.2 空间步长的影响

在一维情况下，PITD的NLE和NPE随时间步长的变化如图2所示。电磁波频率f＝300 MHz，Courant常数S＝1 024，预先选定的整数N＝20，空间采样密度Nλ∈（10，40），电导率σ分别等于3E－4S／m，3E－2S／m和30S／m.

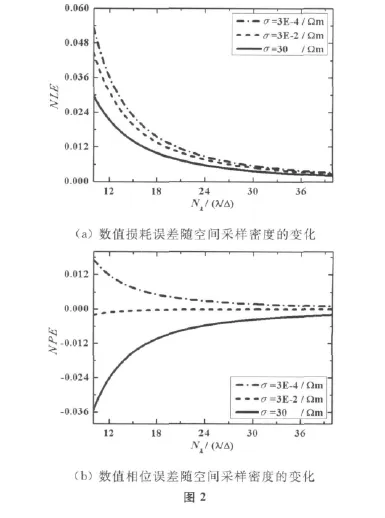
在图2中，随着空间采样密度的增大（空间步长减小），NLE和NPE都将趋近于0.这说明空间步长越小，PITD的数值损耗和数值色散的误差越小。

2.3 电导率的影响

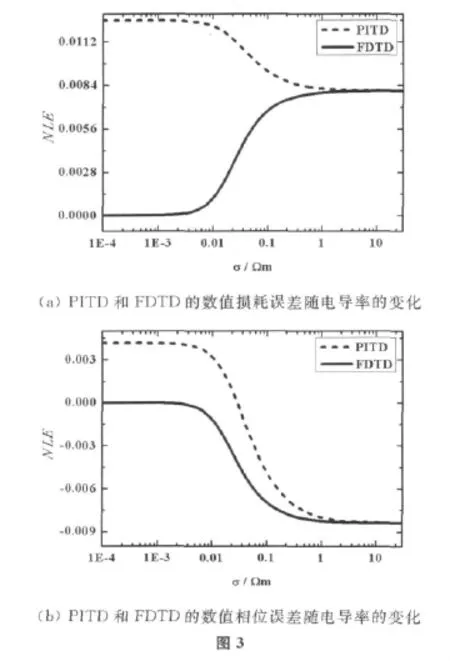
在一维情况下，PITD和FDTD的NLE和NPE随电导率σ的变化如图3所示。电磁波频率f＝300MHz，在PITD中Courant常数S＝1 024，预先选定的整数N＝20.在FDTD中Courant常数S＝1.空间采样密度Nλ＝20，电导率σ∈（1E－4，30）S／m.

在图3（a）中，PITD的NLE大于0，即PITD的数值损耗大于电磁波的真实损耗。随着电导率σ增大，PITD的NLE逐步减小，并和FDTD的NLE趋近于同一极限值。

在图3（b）中，当电导率较小时（σ≪ωε），PITD的NPE大于0.当电导率较大时（σ≥ωε），PITD的NPE小于0，即PITD的数值波速大于电磁波的真实波速。此时，PITD的NPE的绝对值要小于FDTD的NPE的绝对值，即PITD的数值波速比FDTD的数值波速更加接近于电磁波的真实波速。

2.4 数值各向异性

定义数值损耗各向异性Aα和数值相位各向异性Aβ分别为

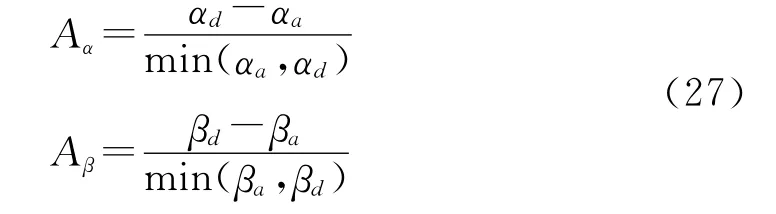
式中：下标d表示数值波沿网格对角线方向传播；下标a表示数值波沿坐标轴方向传播。

在二维和三维情况下，PITD的数值损耗各向异性Aα和数值相位各向异性Aβ分别如图4和图5所示。电磁波频率f＝300MHz，Courant常数S＝1 024，预先选定的整数N＝20，空间采样密度Nλ＝20，电导率σ∈（1E－4，30）S／m，2D表示二维情况，3D表示三维情况。

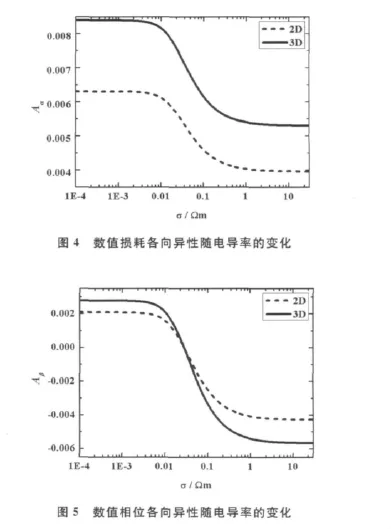
在图4中，三维情况下的Aα大于二维情况下的Aα，即PITD的数值损耗各向异性在三维情况下的值要大于其在二维情况下的值。在图5中，三维情况下的Aβ的绝对值大于二维情况下Aβ的绝对值。当σ＝27.97mS／m时，Aβ＝0.PITD几乎没有数值波速的各向异性。在有耗介质中，FDTD的数值色散研究中也发现了类似的现象［15］。

综合上述分析，有耗介质中PITD的数值损耗和数值色散都基本上不受时间步长的影响。随着空间步长的减小，PITD的数值损耗和数值波速将趋近于电磁波的真实损耗和真实波速。当电导率较大时（σ≥ωε），PITD的数值色散特性要优于FDTD的数值色散特性。随着维数的增加，PITD的数值损耗和数值色散的各向异性将增大。

3.数值算例

计算当绕组中电流突变时，变压器铁心叠片中磁场的瞬态变化。近似认为所有叠片中的磁场相同，只分析其中的一片。假设铁心叠片的长度和宽度远大于厚度，厚度方向为x方向，即磁场H是时间t和空间坐标x的函数。

铁心叠片厚度a＝1mm，电导率σ＝1E7S／m，磁导率μ＝1.2E－3×πH／m.边界条件

和初始条件

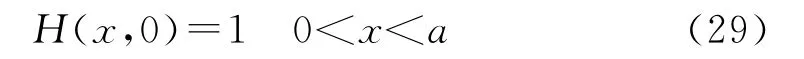
计算t＝5E－3 s时，在x＝0.25mm和x＝0.5mm处磁场强度H 的值。空间步长Δx＝a／1 024.在PITD中Courant常数S＝5E7，预先选定的整数N＝20.在FDTD中Courant常数S＝1.计算结果和CPU时间如表1所示。

表1 PITD和FDTD的计算结果和CPU时间

上述的计算结果表明，PITD的计算误差要小于FDTD的计算误差。相对于FDTD而言，PITD有更快的计算速度和更高的计算精度。由于采用了矩阵计算形式，PITD的计算内存需求较大。应用子域技术可以将PITD的内存需求降低至与FDTD相同的等级［16］。

5.结 论

有耗介质中PITD的数值损耗和数值色散特性的分析结果表明：PITD的数值损耗大于电磁波的真实损耗，其数值波速可以大于电磁波的真实波速。由于PITD色散方程中的时间量（τ）被限制在很小的范围内，PITD的数值损耗和数值色散都基本上不受时间步长的影响。随着空间步长趋近于0，有耗介质中PITD的数值色散方程将趋近于有耗介质中电磁波传播的色散方程。因此，随着空间步长的减小，PITD的数值损耗误差和数值色散误差都将逐步减小。当电导率较小时（σ≪ωε），PITD的数值损耗和数值色散误差大于FDTD的数值损耗和数值色散误差。当电导率较大时，（σ≥ωε）PITD的数值损耗和FDTD的数值损耗趋于一致。由于在电导率较大时，PITD的数值损耗角正切与有耗介质的真实损耗角正切几乎相同，使得PITD的数值波速比FDTD的数值波速更加接近于电磁波的真实波速。数值算例表明：对良导体而言，PITD比FDTD拥有更高的计算精度和更快的计算速度。

［1］葛德彪，闫玉波.电磁波时域有限差分方法［M］.2版.西安：西安电子科技大学出版社，2005.GE Debiao，YAN Yubo.Finite－Difference Time－Domain Method for Electromagnetic Waves［M］.2nd ed.Xi’an：Xidian University Press，2005.（in Chinese）

［2］TAFLOVE A，HAGNESS S C.Computational Electrodynamics：The Finite Difference Time Domain Method ［M］.3rd ed.Norwood：Artech House，2005.

［3］王秉中.计算电磁学［M］.北京：科学出版社，2002.

［4］李太全，田 茂，吴庆麟，等.圆环天线的时域有限差分分析［J］.电波科学学报，2002，17（6）：577－580.LI Taiquan，TIAN Mao，WU Qinglin，et al.Analysis of a round strip antenna using the finite difference time domain method［J］.Chinese Journal of Radio Science，2002，17（6）：577－580.（in Chinese）

［5］艾宝强，褚庆昕，雷振亚.基于FDTD算法的有源集成天线设计［J］.电波科学学报，2004，19（6）：739－741.AI Baoqiang，CHU Qingxin，LEI Zhenya.Design of active integrated antenna based on FDTD method［J］.Chinese Journal of Radio Science，2004，19（6）：739－741.（in Chinese）

［6］胡慧琳，谭云华，朱柏承，等.不同环境影响下共形蝶形天线性能的理论分析［J］.电波科学学报，2010，25（6）：1163－1168.HU Huilin，TAN Yunhua，ZHU Bocheng，et al.Conformal bow－tie antennas in different environments［J］.Chinese Journal of Radio Science，2010，25（6）：1163－1168.（in Chinese）

［7］SULLIVAN D M.Electromagnetic Simulation Using the FDTD Method［M］.New York：IEEE Press，2000.

［8］NAMIKI T，ITO K.3－D ADI－FDTD method unconditionally stable time－domain algorithm for solving full vector Maxwell’s equations［J］.IEEE Transactions on Microwave Theory and Techniques，2000，48（10）：1743－1748.

［9］FU Weiming，TAN E L.Stability and dispersion analysis for ADI－FDTD method in lossy media［J］.IEEE Transactions on Antennas and Propagation，2007，55（4）：1095－1102.

［10］MA Xikui，ZHAO Xintai，ZHAO Yanzhen.A 3－D precise integration time－domain method without the restraints of the Courant－Friedrich－Levy stability condition for the numerical solution of Maxwell’s equations［J］.IEEE Transactions on Microwave Theory and Techniques，2006，54（7）：3026－3037.

［11］ZHONG Wanxie，WILLIAMS F W.A precise timestep integration method［J］.Proc Inst Mech Eng，1994，208（6）：427－430.

［12］JIANG Lele，CHEN Zhizhang，MAO Junfa.On the numerical stability of the precise integration time－domain （PITD）method［J］.IEEE Microwave and Wireless Components Letters，2007，17（7）：471－473.

［13］CHEN Zhizhang，JIANG Lele，MAO Junfa.Numerical dispersion characteristics of the three－dimensional precise integration time－domain method［C］／／ Microwave Symposium IEEE／MTT－S International.Honolulu，2007：1971－1974.

［14］KRUMPHOLZ M，RUSSER P.On the dispersion in TLM and FDTD［J］.IEEE Transactions on Microwave Theory and Techniques，1994，42（7）：1275－1279.

［15］SUN Guilin，TRUEMAN C W.Numerical dispersion and numerical loss in explicit finite－difference timedomain methods in lossy media［J］.IEEE Transactions on Antennas and Propagation，2005，53（11）：3684－3690.

［16］白仲明，赵彦珍，马西奎.子域精细积分方法在求解Maxwell方程组中的应用分析［J］.电工技术学报，2010，25（4）：1－9.BAI Zhongming，ZHAO Yanzhen，MA Xikui.Analysis and application of sub－domain precise integration method for solving Maxwell’s equations［J］.Transactions of China Electrotechnical Society，2010，25（4）：1－9.（in Chinese）