中国股票市场波动率跳跃模型实证研究
金荣载,贺 晗
(韩国釜山国立大学 经济学系,韩国 釜山 609735)
1 研究背景
波动率(Volatility)是衡量标的资产价格或投资回报率变化的剧烈程度的指标。在统计上,它是以复利形式计算的标的资产投资回报率的标准差。在风云变化的金融市场中,各种复杂多变的信息影响着收益率不断波动变化,而新的重要信息往往会使波动率产生超预期剧烈变化,这个现象被称之为跳跃(Jump Behavior)。跳跃过程最开始是由 Press(1967)[1]提出的,他认为股价的变化应包括两个方面:一个是连续的扩散过程;另一个是不连续的跳跃过程。他将泊松(Poisson)跳跃过程加入几何布朗(Brown)运动中,用来描述超预期信息引起的波动率异常变化。诺贝尔经济学奖获得者Merton(1976)[2]成功运用利用几何布朗(Brown)运动和跳跃过程建立了经典的期权B-S定价模型,为期权定价理论作出了杰出贡献。诸多研究都显示使用跳跃过程的模型能够较好的捕捉波动率的异常变动。
自20世纪90年代初中国建立股票市场以来,至今已有了长足的发展,但与发达国家的成熟市场相比,仍然是一个新兴市场,在交易机制、监管制度和法律法规方面都存在不完善、不健全的方面。这些年来,学者们对我国股票市场做了大量的研究,对股票市场的波动也已有较深入的研究,但基于跳跃过程的波动率模型的研究却很鲜见。本文在Chan and Maheu(2002)提出的 GARJI-ND模型基础上建立了EGARJI-ND模型,并根据广义误差分布函数建立了GARJI-GED和EGARJI-GED模型,然后使用上海证券综合指数每日收盘数据对四个模型进行参数估计,最后比较四个模型的拟合效果。
2 文献回顾
Jorion(1988)[3]将泊松跳跃强度设定为常数,建立了混合ARCH跳跃模型 (Mixed ARCH-Jump Model),研究结果显示外汇市场存在跳跃现象,而股票市场这一现象却不明显。
Bates(1996)[4]将 Merton(1976)的跳跃扩散理论和Heston(1993)的SV模型相结合,将跳跃引入随机波动率过程,提出了随机波动率和跳跃模型(Stochastic Volatility Model with Jump Returns),即 SVJ模型,并分析了1984至1991年德国马克兑换美元的外汇选择权。
Duffie,Pan & Singleton(2000)[5]提出了 SVCJ 模型(Stochastic Volatility Model with Independent Jumps in Returns and Volatility)和 SVIJ模型(Stochastic Volatility Model with Correlated Jumps in Returns and Volatility)。这两个模型和Jorion(1988)所建立的模型一样,同样都是假设跳跃事件是独立的,而事实上,跳跃事件往往是非独立事件。SV系列模型并不能很好的描述跳跃过程。
Chan and Maheu (2002)[6]将跳跃-扩散过程引用GARCH模型,建立了自回归跳跃强度模型(Auto-regression Conditional Jump Intensity Model), 即 GARJI模型,并设定其条件分布服从正态分布(Normal Distribution)。因为如果泊松跳跃强度为常数就无法反映跳跃行为的聚集现象,于是Chan and Maheu(2002)将跳跃强度设定为类似自回归的ARMA过程。然后,他们分析了1928年至1984年的道琼斯工业指数(Dow Jones Industrial Average),发现GARJI模型的拟合效果良好。
Chan and Maheu(2004)[7]在原有 GARJI模型的基础上加入过去跳跃的影响,对美国11家公司的股价进行了详细的分析,研究发现无论样本内的适配性或是样本外的波动性预测都达到了较好的效果。
在中国,对跳跃模型实证研究的文献较少。
谢赤和邓艺颖(2003)[8]推导出 GARCH-JUMP 模型,并对利率动态变化中的正常波动与跳跃波动行为进行分析。
童汉飞和刘宏伟(2006)[9]采用 Jump-GARCH 模型对沪深两市A股B股的跳跃性特征进行实证分析,结果表明,该模型能够有效地估计出沪深两市收益率和波动率的跳跃性变化过程,比同样服从正态分布的GARCH模型更合理。
朱波和毛华富(2008)[10]将跳跃过程引入到GARCH模型,对上证A股市场收益的跳跃性进行了分析,并通过蒙特卡洛方法对样本内和样本外进行了预测。
以往对跳跃波动的研究很多都是采用GARCH模型作为理论基础,本文将建立EGARCH形式的模型,并使用两种的条件分布函数,比较分析四个模型的实证效果。
引理 4[7] 假设一个顶点u相邻两个2-点v,w,并且与一个3-圈(u,x,y)相关联,则min{d(x), d(y)}≥4。
3 模型设定
Chan and Maheu(2002)提出的 GARJI模型将影响收益率的信息分为每期互相独立的at和bt,可表示为:

at表示一般信息,它引起收益率的连续性变化,它服从条件均值为0,条件波动率为εt的正态分布,设定GARCH方程,可表示为:
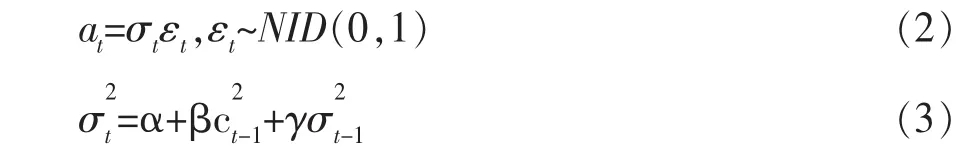
其中,Var(at|It-1)=σt以及 ct-1=at-1+bt-1。
bt表示非一般信息,它引起收益率的跳跃性变化,它服从条件均值为0,条件跳跃强度为λt的泊松跳跃过程,可表示为:

上述(1)至(5)式即为 Chan and Maheu(2002)建立的GARJI模型,其中εt服从正态分布(Normal Distribution),即 εt~NID(0,1),本文将采用此模型并将其命名为GARJI-ND模型。本文将基于 GARCH模型的GARJI-ND模型设定为EGARCH形式,并命名为EGARJI-ND,可以表示为:
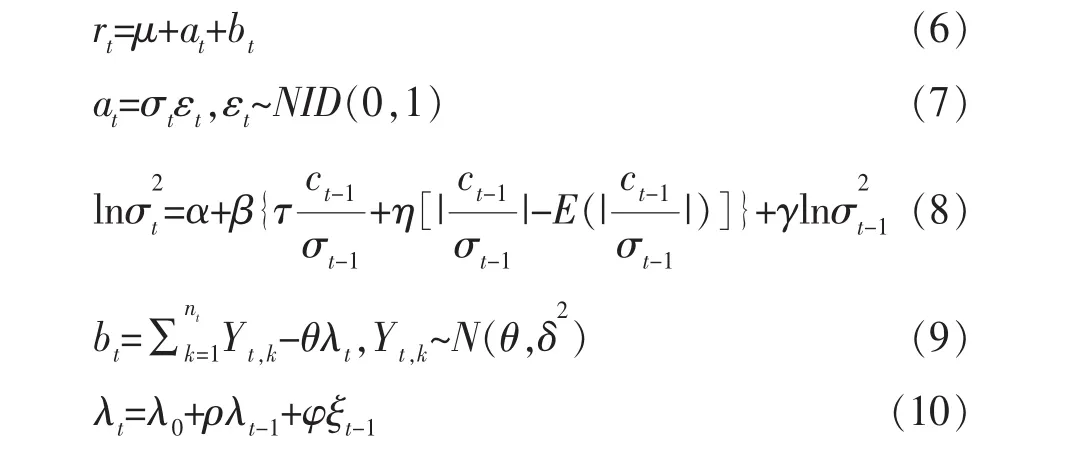
4 实证分析
4.1 数据处理
本文将使用以上四个模型对中国股票市场进行实证分析。相关资料取自上海证券交易所官方网站,数据类型为日收盘价,样本空间为1990年12月19日到2011年05月10日期间所有交易日数据,样本数量为4993个。在获得数据以后,将数据取对数后差分获得指数收益率,具体数据处理办法如下,

(11)式中,rt为指数收益率,pt为第 t期的收盘价,pt-1为第t-1期的收盘价。
中国证券市场较发达国家起步晚,从90年代初设立上海证券综合指数以来,一直摸索前行,一直不断地完善交易制度,建立健全监督机制,构建法律法规体系。直到1999年7月,作为新中国第一部证券法典的《中华人民共和国证券法》正式实施,它的横空出世标志着我国新兴证券市场具备了持续、稳定、健康发展的法律基础。从图1中,可以清楚的发现,在2000年之前,由于股票市场尚未健全,股市经常暴涨暴跌,导致收益率大幅异常波动,为了更好的考察模型效果,本文将数据分为两个样本分别进行分析,第一个样本为1990至1999年共计2253个数据,第二个样本为2000年至2011年共计2740个数据。
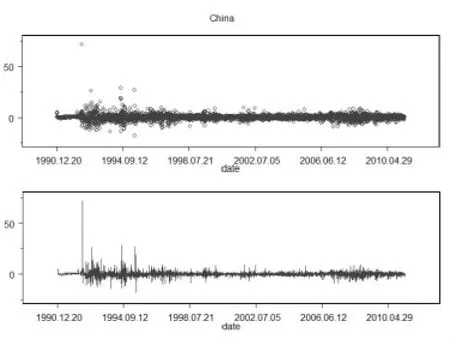
图1 波动图
4.2 统计分析
表1列出了中国上证指数股价指数收益率的基本统计量,可以明显看出样本1(1990年至1999年)的偏度显著大于0,分布向右偏,而样本2(2000年至2011年)的偏度则几乎为0。两个样本的峰度都大于3,皆呈现尖峰厚尾形态。

表1 基本统计量
经过 JB 正态检验(Jarque-Bera),可以发现,中国上证指数股价指数收益率两个样本的JB值均非常大,分别为1092918和2740,且在1%的显著水平上拒绝正态分布的假设,正态分布的概率为0。图2是指数收益率两个样本的QQ图,直线表示正态分布,很明显两个样本的的分布都显著不同于正态分布。指数收益率两个样本的QQ图和JB正态检验都拒绝了正态分布的假设。

图2 QQ-Plot图
在采用GARCH模型之前,必须先验证其是否具有ARCH效应,本文采用LM方法进行检验中国上证指数股价指数收益率两个样本是否存在条件异方差。检验结果如表2中所示,样本1(1990年至1999年)的检验结果为6.582在10%的水平上显著,拒绝不存在ARCH效应的假设;而样本2(2000年至2011年)的检验结果较样本1更为理想,为104.9199,在1%的水平上显著,拒绝不存在ARCH效应的假设。两个样本均通过LM检验,均具有显著的ARCH效应。
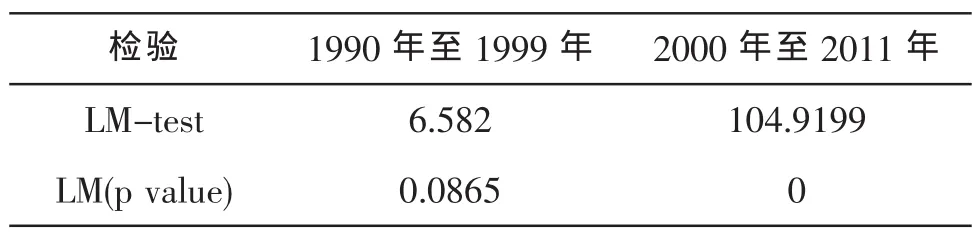
表2 LM检验
4.3 参数估计
本文使用统计学软件SPLUS 8.0根据四个模型分别编写程序,然后导入两组样本数据进行参数估计,第一组样本(1990年至1999年)的参数估计结果如表3所示。第二组样本(1990年至1999年)的参数估计结果如表4所示。
4.4 结果分析
在表3中,四个模型的μ参数都不显著,EGARJIND和EGARCH-GED模型的τ、η和θ参数也不显著,其他参数基本在5%和10%的水平上显著,三个模型的β和γ参数均在1%的水平上显著。通过Ljung-Box检验,四个模型的Q和Q2值在5%水平上均不显著,这说明模型是充分的。总的来说,样本1(1990年至1999年)各模型的拟合效果较好。从参数显著程度上看EGARJI-GED模型的相对最好,其极大似然值最高,模型效果最好。
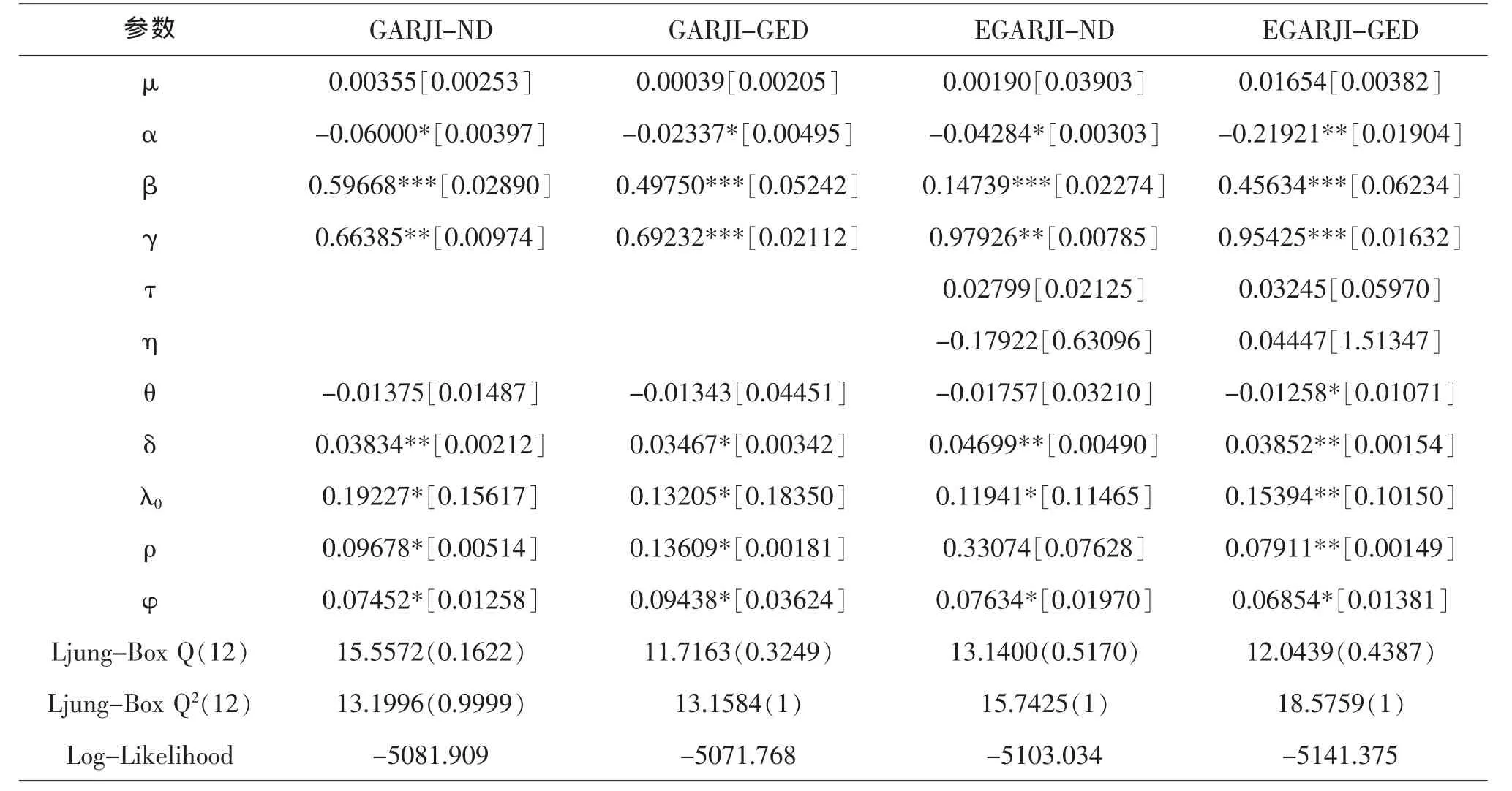
表3 样本1(1990年至1999年)各模型的参数估计结果
在表4中,除了EGARJI-GED模型以外三个模型的μ参数都不显著,EGARJI-ND和EGARCH-GED模型的τ和η参数也基本不显著,四个模型的大部分参数在1%的水平上显著。通过Ljung-Box检验,四个模型的Q和Q2值在5%水平上均不显著,这说明模型是充分的。总的来说,样本2(2000年至2011年)各模型的拟合效果很好。从参数显著程度上看EGARJI-GED模型的相对最好,其极大似然值最高,模型效果最好。
通过表3和表4,比较四个模型的显著程度,可以发现样本1的模型效果明显比样本2效果差。这是因为1999年以前我国的股票市场不成熟,交易制度不完善、监督监管不到位、法律法规不健全导致的,在1995年之前实行的是t+0制度,尚未恢复涨停板制度,那时候市场经常暴涨暴跌,这在一定程度影响了模型的效果。另外,GARJI-GED 和 EGARJI-GED 这两个条件分布服从广义误差分布的模型效果略好于服从正态分布的GARJI-ND和EGARJI-ND模型。这是因为众所周知收益率本来就存在尖峰厚尾 (Fat Tail)的特性,而GED分布具有比正态分布更厚的尾部,所以条件分布服从广义误差分布的模型可以更好的描述这组数据特征。
5 研究结论
本文采集了中国上海证券交易所从1990年12月19日至2011年05月10日期间所有交易日的收盘数据,并将数据分为了两个样本,建立并使用带有跳跃过程和服从不同条件分布的四个模型对样本进行参数估计,通过研究结果可以得出以下几个结论:
第一,含有跳跃过程的四个模型都有良好拟合效果,验证了中国股票市场存在跳跃现象,含有跳跃过程的模型适用于中国股票市场,并有良好的研究和实用价值。
第二,条件分布服从广义误差分布的模型效果好于服从正态分布的模型,更能反映中国股票市场收益率的尖峰厚尾特征,但不能认为服从GED分布的模型就一定优于服从正态分布的模型,只能说明更适合中国股票市场,或者说更适合这套数据。
第三,与GARCH模型相比,EGARCH模型的效果更好,一般复杂的模型包含的参数更多,拟合效果会更好,但是不是越复杂越好,那样会导致过分拟合,降低模型效果。
第四,2000年以前的中国股票市场,市场秩序实际上是非常混乱的,机制不健全,缺乏监督,频繁出台政策,政府不断干预市场,导致市场波动异常,难以获得良好的拟合效果。虽然近年来,中国股票市场有了长足的发展,日趋稳定,但相比发达国家的成熟市场,还是一个新兴的不成熟不完善的市场,在具有中国特色的经济模式下仍需不断摸索前行。
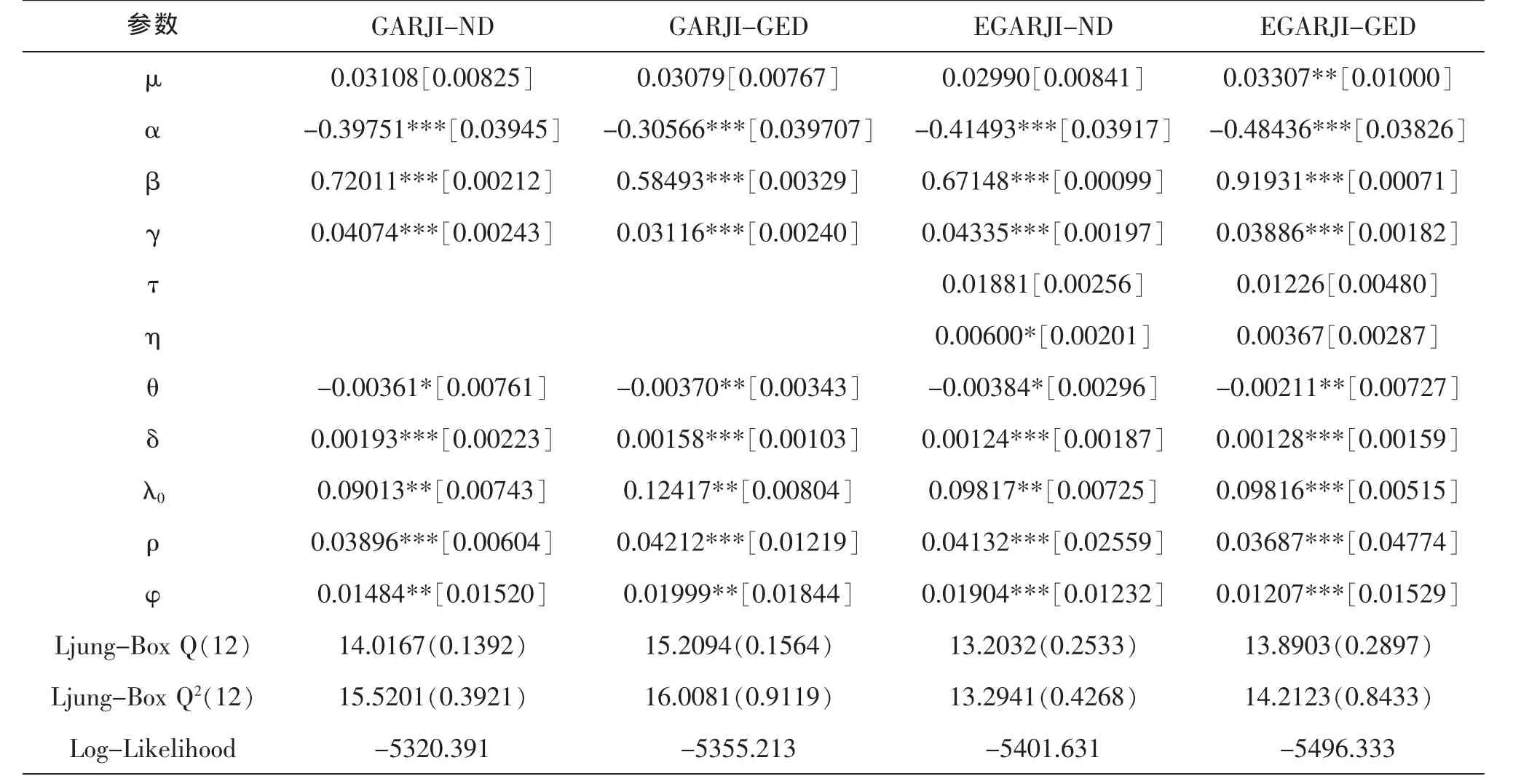
表4 样本1(2000年至2011年)各模型的参数估计结果
[1]Press,S.I.,1967, A compound events model for security prices, Journal of Business,40,317-335.
[2]Merton,R.C.,1976, Option pricing when the underlying stock returns are discontinuous,Journal of Financial Economics,3,125-144.
[3]Jorion, Philippe, 1988, On jump processes in the foreign exchange and stock markets, Reviews of Financial Studies,1,427-445.
[4]Bates(1996)
[5]Duffie,Pan & Singleton,2000,Transform analysis and asset pricing for affine jump diffusions, Econometrica,68 (6),1343-1376.
[6]Chan,W.H.and Maheu,J.M., 2002, Conditional jump dynamics in stock market return,Journal of Business& Economic Statistics,20,377-389.
[7]Maheu, J.M.and McCurdy,T.H.,2004, New arrival,Jump dynamics and volatility components for individul stock returns", the Journal of Finance, 2,755-793.
[8]谢赤和邓艺颖,2003,描述利率动态行为的GARCHJUMP模型,数量经济技术经济研究,3.
[9]童汉飞和刘宏伟,2006,中国股市收益率与波动率跳跃性特征的实证分析,南方经济,5.
[10]朱波和毛华富,2008,跳跃GARCH模型在我国股票市场中的应用研究,Available at CFRN: http://www.cfrn.com.cn /getPaper.do?id=1505

