桩基承台在工程实例中的计算应用

柳艳红

(山西省建筑设计研究院，山西太原 030013)

0 引言

在工程实例中，桩基承台基础应用范围较为广泛。桥梁建筑中多用高桩承台，工业与民用建筑的桩基础一般采用低桩承台;多层与高层建筑是由基础梁、筏形基础的底板兼做承台。也有直接在墙柱下布置独立桩基承台。力求布置桩位时把桩布置在柱下和墙下，否则需要验算基础梁或底板或桩基承台的抗弯、抗冲切、抗剪切承载力。

1 工程概况

山西某建筑为一办公楼，该办公楼与地下车库连为一体。主楼为地下1层，地上12层(不包括屋顶塔楼)，地下1层为5.0 m，地上1 层为3.9 m，其余层为3.7 m，顶层为 5.0 m。总高度 46.500 m。室内外高差0.6 m。采用框架剪力墙结构形式。与主楼相连的地下车库采用柱下钢筋混凝土独立基础，局部条形基础，主楼采用柱下、柱下墙下桩承台基础。

2 桩基承台承载力计算

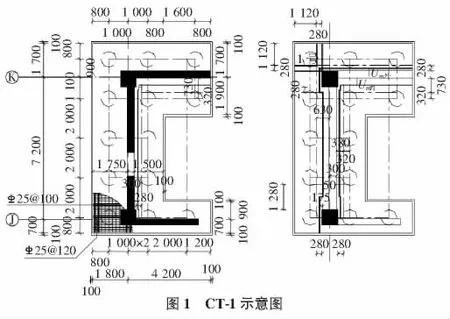
在工程实例的平面布置图中，有几何形状规则柱下两桩承台、三桩承台、四桩承台;有几何形状不规则的柱下、墙下四桩承台、多桩承台。对于几何形状规则的承台用机算程序对其进行承载力的验算校核，对于几何形状不规则的承台用手算对其进行承载力的验算;下面介绍CT-1的承载力计算(见图1)。

2.1 基本资料

1)几何参数。

桩承台的几何尺寸按照其构造要求设置。

柱为正方形:800×800，墙厚为350;C40。

桩为圆形:桩直径 A=800，桩 C35，换算为方桩 bp=0.8×800=640。

承台C35，HRB335桩基重要性系数r0=1.0。

受拉钢筋合力点到承台底边距离:as=100 mm。

进行承载能力极限状态的计算，所以读取荷载效应SATWE基本组合值组合 1.35恒+0.7×1.4活柱墙共同承担的 F=35 174.8 kN。

2)基桩反力计算。

冲切破坏锥体内基桩平均 N单=F/13=35 174.8/13=2 705.75 kN。

2.2 柱、墙对承台的冲切验算

由《建筑桩基技术规范》(5.9.7.1):

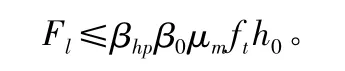
其中，F参数是不计承台与其上土重，在荷载效应基本组合作用下柱墙底的竖向荷载设计值，从机算程序中直接读取;承台H=1 300;ft=1.57 N/mm2;h0=h－as=1.300－0.100=1.200 m;Fl=F－∈Qi;β0=0.84/(λ+0.2)，λ=a0/h0，β0=0.7;线性内插 βhp=1.0×(1.0－0.9)×(1 300－800)/(2 000－800)=0.958。

1)外侧结构构件截面对承台的冲切。

柱边或墙边到桩边水平距离对应为280，280，280，630，1 280，280。

冲切破坏锥体一半有效高度周长相应4 740，1 080，175，5 420，175，1 840。

a0平均=[280×(4 740+1 080+175)+630×5 420+1 280×175+280×1 840]/um。

a0平均=434.3 mm，λ =a0/h0=434.3/1 200=0.362(0.25≤λ≤1.0)。

um外总=13 430 mm，α =0.84/(0.362+0.2)=1.494 7N单=7×2 705.75=18 940.25 kN。

βhpβ0μmfth0=0.958 × 1.494 × 1.57 × 13 430 × 1 200=36 213.709 kN。

7N单=7×2 705.75=18 940.25 kN＜36 213.709 kN。

2)内侧结构构件截面对承台的冲切其计算方法同1)，承台满足抗冲切要求。

3)计算外侧墙侧结构构件截面对承台的冲切其计算方法同1)，承台满足抗冲切要求。

承台抗冲切主要取决于承台板厚度;当承台板较薄时，常在柱边或墙边形成不小于45°破坏锥体;在手算中主要围绕承台冲切破坏锥体来计算。

2.3 角桩对承台的冲切验算

1号角桩对承台的冲切验算，由《建筑桩基技术规范》(5.9.8.1):

N1=[β1x×(C2+a1y/2.0)+β1y×(C1+a1x/2)]×βhp×ft×h0=2 705.75，a1y=0.280 m。

λ1x=a1x/h0=0.280/1.200=0.233= λ1y，β1x=0.56/(λ1x+0.2)=0.56/(0.233+0.2)=1.293。

β1y=β1x，C1=C+1/2×bp=0.800+0.640/2=1.120 m=C2。

因 h=1.300 m，所以 βhp=1.0－[(1.0－0.9)×(1 300－800)/(2 000－800)]=0.958。

将其代入公式可知 2β1x×(C2+a1y/2.0)βhp×ftb×h0=2×1.293×(1 120+280/2)×0.958×1.57×1 200=5 880.92 kN。

2 705.75 kN＜5 880.92 kN，角桩对承台的冲切满足要求。

角桩对承台的冲切，主要取决于承台板厚度;当承台板较薄时，常在角桩处形成不小于45°破坏锥体。

2.4 柱边、桩边承台斜截面受剪验算

由《建筑桩基技术规范》(5.9.10.1):

V＜βhs×α×ftb0×h0，βhs=(800/h0)1/4=0.903 6，axmax=630 mm，λ=axmax/h0=630/1 200=0.525(0.25＜λ＜3)。

α=1.75×(0.525+1.0)=1.147 5，b0×h0=9 600×1 200=11 520 000 mm2。

γ0×V=5N单=5×2 705.75=13 528.75＜βhs×β×ftb0×h0=0.903 6×11 520 000×1.147 5×1.57=18 753.4 kN。

同理，b0=6 000的方向计算也满足斜截面抗剪切要求。

从计算公式中看出，当承台板厚足够时，可以防止发生破坏。

2.5 承台的受弯验算

1)承台底面X方向配钢筋计算。

X左=950 mm，X右=700 mm，取2 m的桩基单元配钢筋计算。

Asx左=γ0×Mx/(0.9×h0×fy)=1.0×2 705.75×0.95/0.9×1 200×300×2=3 967 mm2，φ25@120。

2)承台底面Y方向配钢筋计算。

Y上=600 mm，Y下=1 050 mm，Asy下=γ0×Mx/(0.9×h0×fy)=4 384 mm2，φ25@100。

3)承台的最小配筋面积。

As1min=ρmin×H×1 000=0.150%×1 300×1 000=1 950 mm2。

实际工程中，当承台厚度较小，同时配筋不足时，容易发生弯曲破坏，为了防止发生此类破坏，承台板底部配有足够数量的受弯钢筋。

2.6 柱对承台的局部受压验算

因为承台的混凝土强度等级小于柱的混凝土强度等级，验算柱下承台顶面的局部受压载力。

由《混凝土结构设计规范》6.6.1.1:Fl＜1.35×βc×βl×fc×Aln。

fc=16.7 N/mm2，βc=1.0，取 2 m 的桩基单元计算。

Aln=350×2 000=700 000 mm2，Ab=3Aln，βc=1.732。

Fl=2XN单＜1.35×βc×βl×fc×Aln=1.35×1.732×1.0×16.7×700 000=27 333.558 kN。

柱下承台局部受压承载力满足要求。

2.7 桩对承台的局部受压验算

因为承台的混凝土强度等级不小于桩的混凝土强度等级，所以不用验算桩上承台局部受压承载力。

3 结语

当布置桩位时桩布置不在柱下和墙正下方时，则需要验算基础梁或底板或桩基承台的抗弯、抗冲切、抗剪切承载力。对于几何形状不规则的承台按照上述方法计算，对于承台厚度，底板钢筋足量达到在工程中的应用。

[1]GB 50007-2002，建筑地基基础设计规范[S].

[2]JGJ 94-2008，J 793-2008，建筑桩基技术规范[S].

[3]GB 50010-2010，混凝土结构设计规范[S].

[4]国振喜，曲昭嘉.建筑地基基础设计手册[M].北京:机械工业出版社，2008.