双轮铣槽机起升机构减速器的优化设计研究
杨诗鸿 吴庆鸣
(水利部水利建设管理总站 北京 100038) (武汉大学动力与机械学院 武汉 430072)
黄 玮
(水利部水利建设管理总站 北京 100038)
0 引言
双轮铣槽机因其具有效率高、适应性强、成墙质量好、施工成本低、小型化、经济性好、结构紧凑等特点,在水利防渗工程的施工中应用广泛。双轮铣槽机起升机构是用来保证双轮铣槽机工作装置的正常工作和起升的装置,起升机构方案设计是否合理,是整个双轮铣槽机研制成功的关键。
双轮铣起升减速器内置于卷筒内,卷筒尺寸对减速机的尺寸、体积有限制,要求减速器结构尺寸小。另外,要求最低下降速度时,发动机的转速高于50r/min为好。按照常规设计方法难以获得理想的结果,因此对双输入减速器进行优化设计,对提高双轮铣槽机工作性能、缩小体积、减少重量、节约原材料,以及降低成本都具有重要的现实意义[1]。
目前,对于多级的齿轮传动优化研究,常将传动比的优化分配与齿轮传动参数的优选分开,这种方法存在着一定的局限性[2]。本文建立的以最小体积和最大传动比为目标的多目标优化模型,将等强度分配传动比作为一个约束条件,不是优先对传动比进行分配,而是在优化过程中得到传动比和各级齿轮传动的参数,使传动比满足等强度条件。
1 优化模型建立
1.1 优化目标函数
1.1.1 体积优化目标函数
为了减轻减速器的体积和重量,降低产品成本,另外,由于双输入行星减速器安装在卷筒内,本身结构尺寸就受限制,因此以其最小外轮廓尺寸为目标函数。对于行星齿轮传动来说,在其内齿轮外轮廓尺寸最小时,其外轮廓所围的体积也最小,因此以多级行星齿轮传动的内齿轮体积之和建立目标函数:

式中 Bi——第i级齿宽。
1.1.2 传动比优化目标函数
双输入行星减速器一级太阳轮单独输入时,随着其传动比的增大,发动机的最低输入转速增大,起升机构的低速稳定性增高,传动比优化的目标是取其最大值,其函数表示为:
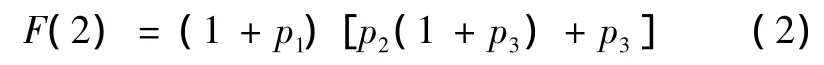
1.2 设计变量
影响传动比优化和体积优化的参数有各级传动比,各级齿轮的齿宽、模数、齿数以及行星轮的个数,在本文中,根据初步方案设计和经验,确定第一、第二、第三级行星轮个数为 3、3、4,因此选择参数 B1、B2、B3、m1、m2、m3、za1、za2、za3、p1、p2、p3为优化设计变量,则有

1.3 约束条件
根据行星齿轮传动的特点,双输入行星减速机优化设计需满足行星齿轮设计的基本条件,如传动比等强度原则、最小模数、最小齿数、齿宽与模数的关系、齿轮疲劳强度、安装条件、传动比条件等。
1.3.1 等强度分配原则[3]
一般来说,传动比的分配都是以各级外啮合接触强度相等为原则进行的,通过约束条件控制优化过程中参数的取值,使得到的优化尽可能满足等强度分配,这样可避免传统优化先按等强度分配的缺陷。

1.3.2 传动比要求
双输入行星齿轮减速机构传动比应大于发动机50r/min时对应的传动比i,则有:

另外,在多级行星传动中,低速级传动比常取4~5.6(总传动比较大时取大值,反之取小值),中间级传动比范围一般为5~7.1,高速级的传动比范围较大,为4~9左右,因此可得各级传动比约束为
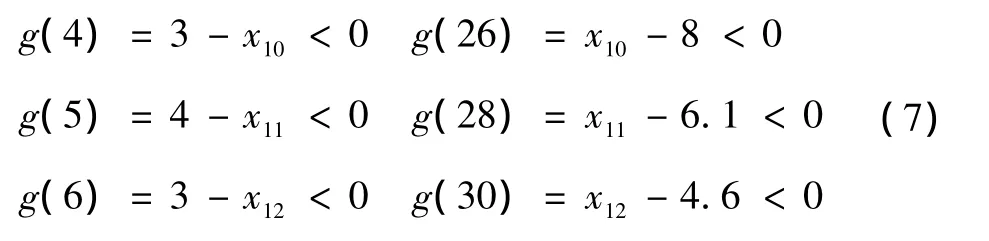
1.3.3 配齿条件限制
直齿非变位或高度变位的行星齿轮的同心条件为2zc=zb-za,行星轮系必须满足安装条件(za+zb)/np=c,其中np、c分别为行星轮数和非零整数,这种约束条件在优化程序中难以实现。本文将根据优化结果,通过配齿计算来满足上述约束条件。为了避免各行星轮产生相互碰撞,必须保证它们齿顶之间在其连心线上有一定间隙,即两行星轮的齿顶圆半径之和应小于其中心距Lc。
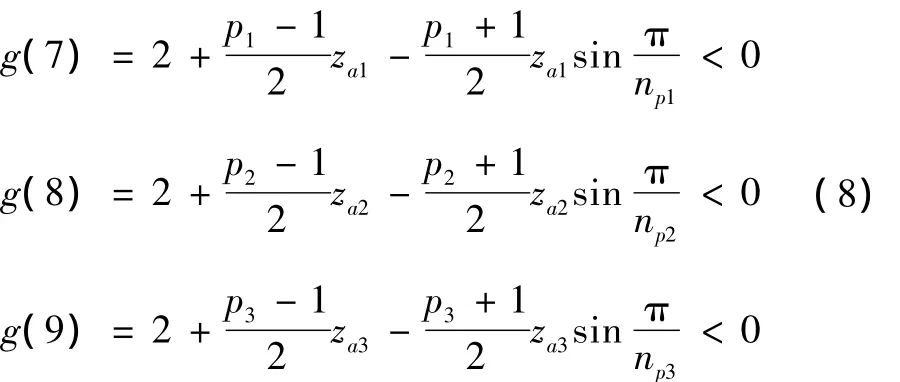
1.3.4 强度条件
一般来说,行星轮系的内啮合承载能力高于外啮合,在本文中,主要对外啮合进行强度校核。
对于双输入行星减速器有如下强度条件,可以得到6个不等式约束:
接触疲劳强度

弯曲疲劳强度

1.3.5 径向尺寸要求[4]
内齿圈分度圆直径基本上决定了行星减速器的外形尺寸,对于多级行星齿轮的设计一般还要求各级内齿圈的直径相近,以使径向尺寸最小。

另外,由于卷筒尺寸已确定,减速器安装于卷筒内,因此第三级的齿圈尺寸受限制,初步确定第三级齿圈的分度圆直径不超过400mm,则有

1.3.6 其他条件约束
根据直齿标准齿轮不根切原理,齿数应大于17,则有:

齿厚与模数之间的关系必须满足5m<B<17m,模数一般要求应大于2mm,则有:
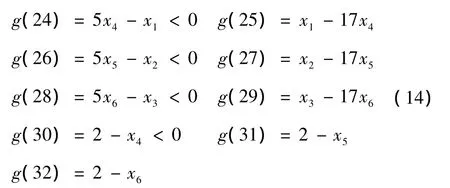
2 优化方法选择
双输入行星减速器的优化是一个多目标、多自变量的优化问题,优化的理想结果是体积最小同时获得最大的传动,即F1(x)→min且F2(x)→max,由于具有两个性质各异的目标函数,本文将采用乘除法来处理多目标优化问题。乘除法的基本原理是:在全部t个分目标函数中,有s个分目标函数希望函数值越小越好,另外(t-s)个分目标函数希望函数值越大越好,则同意目标函数为

式中 wj为各分目标的加权系数。
双输入行星减速器的优化是不等式约束非线性优化问题,而且齿数、模数是离散变量,是既有离散变量又有连续变量的混合优化问题,由于外点罚函数法的初始点既可在可行域内也可在可行域外,因此本文可采用此方法将约束优化问题转化为无约束优化问题。
由于外点罚函数法主要是针对连续变量的优化,而双输入行星减速器优化中齿数是整型变量,模数是离散变量,因此需要对外点罚函数进行改进。本文将外点罚函数法与离散变量网格法结合,其主要原理如下:对于非连续变量xi,利用外点罚函数法处理连续变量的优势,先获得连续最优解X*,若的整数部分为[],则[]和[]+1便是最接近的两个整型点,若X*是n维设计空间,则每个分量都可以找个[]和[]+1两个离散值点,从而可以获得2n个离散点,对2n个离散点采用网格法进行寻优,即可获得圆整后的最优解[1,4]。
对于双输入行星减速器的优化,采用分层网格法进行优化计算:ⓐ将所有变量看成是连续变量,利用外点罚函数法获得最优解X*,对模数进行网格法寻优;ⓑ将模数设为固定值,对其余变量再进行一次优化,然后对齿数进行网格法寻优;ⓒ对其余变量再做一次优化,获得最终的最优解。
3 基于Matlab优化求解
在Matlab平台下,编制求解程序,求解优化模型,优化的总体流程如下图所示[5]。

双输入行星减速器优化流程图
优化得到的传动比为310.38,比原设计提高了6.98%,根据之前各级传动比的约束,传动比最大值可达348.84,优化的传动比较理想;体积优化结果为1.002×107mm3,减少了13.79%,而且第三级齿圈的径向尺寸小于原设计,另外原设计不满足的传动比等强度分配原则,优化结果满足等强度约束条件,因此优化结果较为理想。
4 结论
本文根据双轮铣槽机的设计要求,分析了双输入行星减速器的设计目标,建立了以体积最小、传动比最大为目标的非线性多目标优化模型,并运用外点罚函数法和离散网格法对双输入行星减速器进行了优化,获得了很好的优化结果,为提高双输入行星减速器的设计质量提供了依据。
1 张斌.双轮铣槽机起升机构的研究[D].武汉大学,2010.
2 唐军,胡晓兵,王波,等.起升机构减速器及卷筒的优化设计[J].机械工程师,2006(3).
3 张涵,官德娟.行星齿轮减速器多目标优化设计研究[J].电子机械工程,2006(3).
4 管洪杰,张念淮,刘保国.三级行星减速器优化设计[J].机械传动,2008(3).
5 苗君明,佟刚.基于Matlab的齿轮减速器优化设计[J].沈阳航空工业学院学报,2005(5).

