网络流量预测模型研究进展
邱 婧,夏靖波,吴吉祥
(空军工程大学 电讯工程学院,陕西 西安710077)
0 引 言
网络流量预测是流量工程、拥塞控制、网络业务管理的核心问题。近年来的研究发现,网络流量即使在流量突变时也呈现出一定的变化规律,这使得对网络流量序列进行分析、预测成为可能。一旦能够较早准确地预测出流量的变化趋势,进而设计出高效的拥塞控制机制,合理地进行资源分配与调度,即可减少或避免拥塞的发生,提高网络资源的利用率。因此,网络流量的预测一直是研究人员所关心的重要课题,也是难度较大的研究领域之一。网络流量预测就是针对网络的流量数据,通过所建立的数学模型对流量进行预测。一个理想的网络流量模型应该满足以下几个方面的要求:①能够准确地刻画与网络流量相关的统计特性;②在计算上是高效可行的;③可以应用在与网络设计相关的分析过程中。
国内外专家根据网络流量特性的不断发展陆续提出了许多模型,有按预测长短分类的,有按平稳性分类的等,这些模型拥有各自的优缺点。但是随着网络的不断发展以及对网络流量特性的深入研究后发现,实际网络中的流量具有长相关、自相似、单分形和多分形[1-2]等多种特性,以往单一模型不能完全对网络流量的这些特性进行兼顾,通过将不同的单一模型进行组合后对流量进行预测成为新的研究方向。因此网络流量预测按所使用的模型可分为单一预测模型和组合预测模型,单一预测模型又可分为线性预测和非线性预测;组合预测模型综合了2种或2种以上单一模型,利用多个不同的模型刻画流量不同的特性,然后将它们组合起来得到拟合流量来预测网络流量。本文将围绕单一预测模型和组合预测模型的分类和各自的特点展开讨论。
1 单一预测模型
网络流量数据属于时间序列数据,通过当前时刻的一组观测流量数据Xn-i(i=0,1,2,…,n)建立相应的数学模型来计算来某一时刻的流量Xn+k。传统的网络流量预测模型都是单一预测模型,即采用一种数学模型对网络流量数据进行预测,单一预测模型根据模型输入输出数据之间的关系分为线性预测模型和非线性预测模型。
1.1 单一线性预测模型
早期研究认为网络流量服从Poisson分布或近似为Markov过程,一般多采用基于自回归 (AR)或自回归滑动平均 (ARMA)[3]的线性预测模型。近年来对网络流量进一步研究后发现网络流量具有自相似性[1],人们开始采用能够表征长相关性和突发性的自相似模型来描述网络流量,各种基于自相似性的流量模型被不断地提出。文献 [4-5]提出的自回归求和滑动平均模型 (ARIMA)模型基于ARMA模型,通过若干次差分使序列更平稳,较之传统随机模型能更好地描述网络流量多构性、突发连续性和自相似性等特征,它作为线性预测的代表得到了广泛的应用,但ARIMA模型只能用于处理齐次的非平稳性过程,不能对网络流量进行长期预测。文献 [6]使用长相关模型差分自回归求和滑动平均模型 (FARIMA),利用 “后向预报”技术对序列进行分析反滤波,在参数估计中利用粗、精估计结合的方法建立模型,将FARIMA过程视为分形高斯噪声经过一个以ARMA参数为滤波器系数进行滤波的结果,因参数简单而成为自相似网络流量建模的主要工具,但是计算量比较大。
单一线性预测模型由于数学理论比较完善,应用十分广泛,较好地满足了早期网络的建模需求,在网络设计、维护、管理和性能分析等方面发挥了很大的作用。但是随着网络应用的不断增多,人们研究发现,网络流量的某些特性已远远超出传统队列中的Poisson和Markov流量模型的框架,用线性方法来预测非线型的网络流量在理论上就存在不足,其预测精度不高。
1.2 单一非线性预测模型
大规模网络本身是复杂非线性系统,同时受多种外界因素影响,不仅呈现出非平稳动态随机变化特性,且其内部运行关系也很难确定。随着智能算法的不断发展,其良好的非线性映射能力、灵活有效地学习方式,在预测领域的应用中表现出较大的优势和潜力,如小波分析、神经网络理论、混沌理论、支持向量机方法等。典型的非线性预测方法包括神经 网络模型[7]、灰色模型[8]、混沌模型[9-11]、支持向量机模型[12]等。神经网络结构具有很强的自学习能力和逼近任意非线性系统的能力。灰色模型通过对已知数据的生成变换,挖掘隐含在其中的规律,由于网络中一条链路或路径流量的影响因素很多,不完全明确或无法量化,因此便可将网络中某一条链路流量看作一个灰数,用灰色理论分析。混沌模型中基于最大Lyapunov指数的预测方法是直接根据数据序列本身所蕴含的规律来进行预测,不需要实现建立主观的分析模型,它具有精度高、可信度高的优点。支持向量机以结构风险最小化原则取代传统机器学习方法中的经验风险最小化原则,具有很好的泛化能力,在小样本的机器学习中显示出了优异的性能,它克服了神经网络方法固有的局部极小、过学习以及结构和类型的选择过分依赖经验等缺陷,已经被广泛应用于非线性时间序列预测中,并取得了良好的效果。
但目前来说,神经网络模型还有很多有待改进的地方,其性能还不十分稳定,而且预测时需要大量的训练样本和迭代,还要不断修正模型,从而增加了时间和空间复杂性。此外,单、多步长的预测关系,短长范围的预测关系及神经网络自身等还有很多工作以待研究。灰色模型由于本身的存在缺陷,使其仅能适用原始数据序列按指数规律变化且变化速度不快的场合,而当时间序列数据呈不规则波动变化时,数据拟合效果就显得不够理想,且预测值精度不高[13]。采用支持向量机求解问题需要选择一个核函数,目前对核函数及其参数的选择仍没有一个统一的模式。支持向量机算法模型的选择还只能是凭借经验、实验对比、大范围搜索或者利用交叉验证功能进行寻优。而基于小波分析模型的预测实时性较差[14-15]。
2 组合预测模型
随着网络的普及和P2P等新应用的不断出现,网络业务需求激增,影响网络流量特性的不确定因素 (新应用、协议结构变化等)非常多,非线性、多时间尺度的变化越来越明显,使得网络流量在一定程度上呈现出随机和不确定的特性,这些特性可以通过突发性、长相关、周期性和混沌性等来描述。采用单一的预测模型来刻画网络流量的原始特性,进行预测时不可避免地会产生较大的误差。
因此选择合适的模型是网络流量预测面临的关键问题。就一个问题的预测而言,可以选用不同的预测方法,通过各种预测模型从不同角度对系统进行模拟,它们之间有着相互联系的一面,组合预测模型就是把不同的预测模型综合起来,取长补短,从而达到提高预测精度和增加预测可靠性的效果。近年来,不断有学者根据复杂网络流量存在多个特性的事实,采用多个不同的单一预测模型刻画相应的特性,然后将它们有机组合起来得到拟合流量来预测网络业务流量,大都取得不错的预测效果。
对于网络流量的组合预测有多种形式,根据各个模型之间的组合方式不同,组合预测模型大致可分为3类:线性组合模型、优化组合模型、分解重构组合模型。
2.1 线性组合模型
线性组合模型就是把不同的单一预测模型组合起来,综合利用各预测模型所提供的信息,以适当的加权平均形式得出组合预测值,如图1所示。
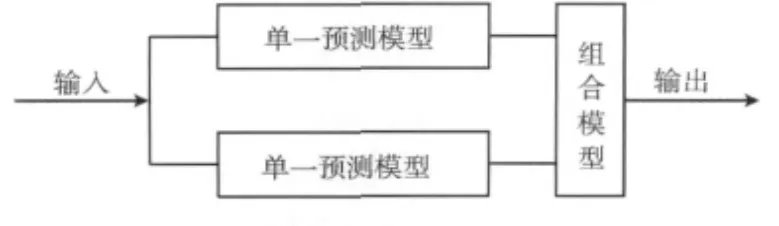
图1 线性组合模型
文献 [8]在一定条件下分别得到灰色模型和神经网络模型的预测值,再对两者的预测值进行加权平均最后得到组合模型的最优预测值。两者的组合既能克服神经网络的局限性,又能在长期预测中获得较为精确的预测值。
文献 [16]根据神经网络的自学习能力和模糊逻辑的动态性和及时性等特点,将模糊逻辑和神经网络有机的结合起来,利用一个具有五层结构的模糊神经网络 (FNN)作为新模型进行网络流量预测。仿真结果表明,FNN能够很好的预测复杂网络业务,比单独的神经网络模型具有更快的收敛速度和更好的预测性能,这为复杂网络的网络业务流量的预测研究提供了一种有效途径。
线性组合模型是组合预测模型中最简单的组合方式,它利用不同单一预测模型从不同的角度提供各个方面有用的信息,博采众长,对各个单一模型得到的预测值进行加权组合,从而得到整个组合模型的预测值。线性组合预侧的关键是如何求出加权系数,使得组合预测模型更加有效地提高预测精度。
2.2 优化组合模型
优化组合模型有两种实现方式,一种是先用某种方法对流量序列数据进行预处理,再用单一预测模型对处理后的序列进行预测;另一种是先建立单一预测模型,再用其它方法对模型进行修正,最后用修正之后的模型进行预测。优化组合模型通过一系列的预处理和修正提取出真正能够反映网络流量特性的信息建立起预测模型,从而提高了模型的预测性能,如图2所示。
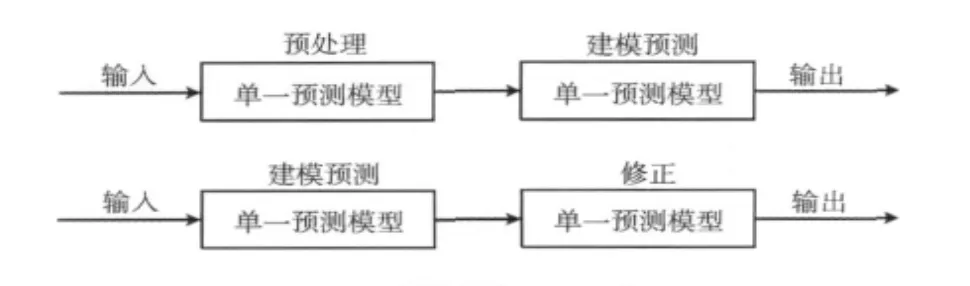
图2 优化组合模型
目前的研究结果表明网络流量存在着混沌特性,混沌支持向量机预测模型首先根据混沌系统的相空间重构理论求出训练历史数据的最佳嵌入维数d和时延S,生成训练样本;再对生成的训练样本进行归一化处理,以便提高收敛速度、缩短训练时间;最后生成的训练样本利用支持向量机回归进行训练,得到预测模型。文献 [17]采用相空间重构理论计算实际流量的延时、嵌入维数和Lyapunov指数,证实网络流量存在混沌现象;据此建立混沌-支持向量机预测模型,并确定训练样本对实际网络流量数据进行预测。
文献 [13]根据网络流量历史数据用灰色模型GM(1,1)进行预测,并用自适应过滤法[18]对GM (1,1)预测时产生的残差进行修正,从而达到较高的预测精度。该方法综合了GM (1,1)预测所需原始数据少、方法简单等特点,具有较高的应用价值。
目前对于网络流量的预测多采用智能算法如神经网络、支持向量机等,但是智能算法对样本数据的要求较高,而网络流量本身又具有复杂的行为特性,给建模和计算都带来了一定的难度。优化组合模型则通过对样本数据进行一定的处理,提取出对建模有用的确定性数据,或者对初始预测模型进行修正,然后建立组合预测模型对网络流量进行预测,降低了算法的难度和预测模型的复杂度,提高了预测精度和效率。
2.3 分解重构组合模型
网络流量具有较高的复杂性、非线性、不平稳特性,而小波变换的核心是多尺度分析,它通过小波基的伸缩变换,研究信号各个尺度层次上的信息。小波变换在信号分析方面显示了独特的优势,被广泛应用于理论研究中。分解重构组合模型就是通过离散小波对网络流量序列进行多尺度分解和单支重构,获得1个逼近信号和多个细节信号,对逼近信号和细节信号分别用不同的单一预测模型进行预测,最后把各个预测的信号通过拟合生成流量的最终预测结果,如图3所示。
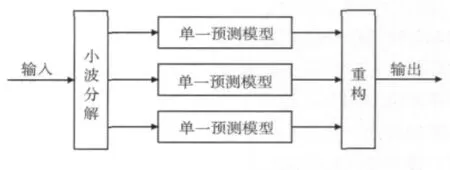
图3 分解重构组合模型
网络流量序列经过小波分解后,可采用单一线性或者非线性预测模型对分解信号序列进行预测,目前分解重构组合模型主要的结合方式有:
(1)小波变换与线性预测模型结合:文献 [19]将网络流量通过小波分解成不同尺度下的逼近信号和细节信号,然后分别单支重构成低频序列和高频序列。根据低频序列和高频序列的不同特性,分别采用自回归模型 (AR)和线性最小均方误差估计 (LMMSE)[20]对未来网络流量进行预测,最后重新组合生成预测流量。
(2)小波变换与神经网络结合:文献 [21]提出了一种基于小波变换和FIR神经网络的广域网网络流量预测模型,首先采用小波分解把网络流量数据分解成小波系数和尺度系数,即高频系数和低频系数,将这些不同频率成分的系数单支重构为高频流量分量和低频流量分量,再用FIR神经网络对这些分量分别进行预测,将合成之后的结果作为原始网络流量的预测值。文献 [22]提出了一种基于Elman递归神经网络、小波和自回归的网络流量组合预测模型,将非线性时间序列施行小波变换,对具有平稳特征的尺度系数序列用AR模型进行预测;而对体现了网络流量非线性、非平稳特性的小波系数序列使用Elman递归神经网络进行预测,最后通过Mallat算法重构得到网络流量的预测值。还有基于下一代网络 (NGN)的运行环境[23],将神经网络中的转移函数使用小波函数来替代从而构建出另一种小波神经网络 (WNN),同时使用小波多尺度变换方法将原始流量信号分解成不同频率成分的分量信号并将其送到该模型中进行预测。
(3)小波变换与支持向量机结合:文献 [24]首先将原始流量数据时间序列进行小波分解,并将分解得到的近似部分和各细节部分分别单支重构到原级别上;对各个重构后的序列分别用最小二乘支持向量机进行预测,将各个预测结果重构后得到对原始序列的预测结果。
(4)小波变换与灰色模型结合:文献 [25]通过将小波分解的平稳化处理优点和灰色理论中的平移处理优点结合起来,根据各自的预测原理建立了基于灰色小波的网络流量预测模型。模型首先对网络流量序列进行小波分解,分解后的时间序列分别用灰色理论进行平移预处理,然后对预处理后的序列数据进行预测并重构,从而得到原始时间序列的预测值。
流量序列经过小波多尺度分解后,可以得到近似信号序列和各层的细节信号序列,近似信号序列包含了流量的趋势项部分,对该部分的预测最为重要;各层的细节信号是网络的突发部分,体现了流量的局部特征,可以作为对趋势项的补充。通过小波分解使网络流量的复杂特性得到分解,得到特性相对比较单一、更加易于预测的时间序列,在此基础上建立能够刻画对应序列特性的模型,得到能够充分反映网路流量总体趋势和细节的预测值。因此分解重构组合模型较之线性组合模型和优化组合模型来说,对于网络流量的预测更加全面、精确。目前对于组合预测模型的研究大多是建立在小波分解的基础上,国内外学者正尝试用不同的预测模型对分解后的分支序列进行预测,再将各预测值进行拟合以得到更加精确、可靠的预测值。
应用组合预测模型来预测网络流量的时候,可以拟合多个模型的优点,更全面地刻画复杂的流量特性,相对于单一预测模型来说,具有更好的预测效果。基于此,可以认为采用组合预测模型可以更加准确、全面地描述和预测实际网络流量。目前,这方面的工作仍在探讨与研究中。
3 结束语
流量预测作为记录和反映网络及其用户活动的重要载体和为网络中带宽分配、流量控制、选路控制、接纳控制、安全管理提供有效依据,是目前研究的一个热点问题。组合预测模型是流量预测的研究趋势,怎样建立一个合适的、能够精确预测网络流量的模型是有待进一步解决的问题。
鉴于网络流量本身具有的复杂性与动态性,对网络流量进行预测应更多地从以下几方面考虑:
(1)组合预测模型的工作仍在探讨与研究中,建立组合模型的主要难点在于确定合适的网络业务特性及其使用方法;
(2)目前大多数流量预测模型仅仅是对历史数据的分析,但是在实时网络流量中由于流量数据的不确定性致使预测模型算法复杂,预测精度不高,因此有必要进一步探索能够精确预测实时网络流量的预测模型;
(3)目前网络流量预测都是针对互联网网络流量,对于无线通信网络与移动通信网络流量是否也可以用相关模型进行预测是值得进一步探讨的问题。
[1]YI Q,Skieewicz J,Dinda P.An empirical study of the multiscale predictability of network traffic [C].IEEE International Symposium on High Performance Distributed Computing,2004:66-76.
[2]Rezaul K M,Grout V.An overview of long-range dependent network traffic engineering and analysis [C].Nantes,France:Charaeteristics,Simulation,Modelling and Control in Proceedings of the 2nd International Conference on Performance Evaluation Method Ologies and Tools,2007:1-10.
[3]Swiecimka P O,KwaPien J,Drozdz S.Wavelet versus descended fluctuation analysis of multifractal structures [J].Physical Review,2006,74 (1):188-190.
[4]YU Guoqiang,ZHANG Changshui.Switching ARIMA model based forecasting for traffic flow [C].Proc of ICASSP.Piscataway:IEEE,2004:429-432.
[5]Zare M H,Masnadi-Shirazi M A.Arima model for network traffic prediction and anomaly detection [C].ITSim’08.Kuala Lumpur:IEEE Press,2008:1-6.
[6]LI Shining,YAN Yan,QIN Zheng.Network traffic forecast based on Farima model [J].Computer Engineering and Applications,2006,42 (29):148-150 (in Chinese).[李士宁,闫焱,覃征.基于FARIMA模型的网络流量预测 [J].计算机工程与应用,2006,42 (29):148-150.]
[7]Junsong W,Jiukun W,Maohu Z,et al.Prediction of internettraffic based on Elman neural network [C].Guilin:Chinese Control and Deeision Conferenee,2009:1248-1252.
[8]CAO Jianhua,LIU Yuan,DAI Yue.Network traffic prediction based on error advanced DGM (1,1)model [C].International Conference on Wireless Communications Networking and Mobile Computing,2007:6353-6356.
[9]DOU L,Binghui J,Haige X.The on-line predietion of selfsimilar traffic based on chaos theory [C].International Conference on Wireless Communications Networking and Mobile Computing,2006:1-4.
[10]LIU R,SHEN J,ZHANG D,et al.Chaotic forecast of the signaling traffic in NGN [C].China:Control Conference,2008:198-201.
[11]Jinjun L,Zhiquan W.Internet traffic dalaflos forecast by RBF neural network based on phase srace reconstruction [J].Transactions of Nanjing University of Aeronautics & Astronautics,2006,23 (4):316-322.
[12]WANG H F,HU D J.Comparison of SVM and LS-SVM for regression [C].International Conference on Neural Networks and Brain,2005.
[13]MA Hualin,LI Cuifeng,ZHANG Liyan.Network traffic prediction based on grey model and adaptive filter [J].Computer Engineering,2009,35 (1):130-131 (in Chinese).[马华林,李翠凤,张立燕.基于灰色模型和自适应过滤的网络流量预测 [J].计算机工程,2009,35 (1):130-131.]
[14]YANG Jiahai, WU Jianping, AN Changqing. Internet measurement theory and application [M].Beijing:Posts & Telecom Press,1999 (in Chinese).[杨家海,吴建平,安常青.互联网络测量理论与应用 [M].北京:人民邮电出版社,2009.]
[15] WEN Chenglin,ZHOU Donghua. Multiscale estimation theory and its application [M].Beijing:Tsinghua University Press,2002(in Chinese).[文成林,周东华.多尺度估计理论及其应用 [M].北京:清华大学出版社,2002.]
[16]WANG Zhaoxia,HAO Tingzhu,CHEN Zengqiang,et al.Predicting nonlinear network using fuzzy neural network [C].Information Communications and Signal and the Fourth Pacific Rim Conference on Multimedia,2003:1697-1701.
[17]LUO Yunqian,XIA Jingbo,WANG Huanbi.Application of
chaos-support vector machine regression in traffic prediction[J].Computer Science,2009,36 (7):244-245 (in Chinese).[罗赟骞,夏靖波,王焕彬.混沌-支持向量机回归在流量预测中的应用研究 [J].计算机科学,2009,36(7):244-245.]
[18]LIU Xianxing,DING Fei,HU Zhentao,et al.Adaptive filtering algorithm of noise variances based on modified“Current”statistical model [J].Chinese of Journal Electronics,2006,15 (2):265-266.
[19]LI Xiaohang,LIU Yuan,LIU Yuanzhen.Research on network traffic combination prediction method based on wavelet multi-scale analysis [J]. Microelectronics & Computer,2008,25 (1):130-133 (in Chinese).[李小航,刘渊,刘元珍.基于小波多尺度分析的网络流量组合预测方法研究 [J].微电子学与计算机,2008,25 (1):130-133.]
[20]Gospodinov M.Wavelet-based analysis of simulated net-work traffic [C].Bulgaria:International Conference on Computer Systems and Technologies-Comp Sys Tech University of Veliko Tarnovo,2006.
[21]TIAN Nili,YU Li.AWAN network traffic prediction model based on wavelet transform and FIR neural networks [J].Journal of Electronics &Information Teehnology,2008,30(10):2549 (in Chinese).[田妮莉,喻莉.一种基于小波变换和FIR神经网络的广域网网络流量预测模型 [J].电子与信息学报,2008,30 (10):2549.]
[22]LIU Yuan,YAO Meng.Combination prediction model of network traffic based on recurrent neural networks [J].Computer Engineering and Design,2008,29 (3):700 (in Chinese).[刘渊,姚萌.基于递归神经网络的网络流量组合预测模型 [J].计算机工程与设计,2008,29(3):700.]
[23]ZHAO Qigang,FANG Xuming,LI Qunzhan,et al.WNN based NGN traffic prediction [R].Chengdu:Proc ISADS,2005:230-234.
[24]LIU Yuan,WANG Peng.Combining wavelet transform and Bayesian least squares support vector machines to predict network traffic [J].Application Research of Computers,2009,26 (6):2229-2231 (in Chinese).[刘渊,王鹏.融合小波变换与贝叶斯LS-SVM的网络流量预测 [J].计算机应用研究,2009,26 (6):2229-2231.]
[25]GONG Linming,ZHANG Zhenguo.Combination prediction model to network traffic based on grey-wavelet [J].Computer Engineering and Design,2010,31 (8):1660-1661 (in Chinese).[巩林明,张振国.基于灰色小波的网络流量组合预测模型 [J].计算机工程与设计,2010,31 (8):1660-1661.]

