基于数模混合的真随机数发生器

叶少康，李 峥

（解放军信息工程大学 电子技术学院，河南 郑州450004）

0 引 言

随机数发生器 （RNG）在许多方面有着广泛的应用，如模拟与仿真系统、神经网络的计算、数字系统的内建自检测、分布与统计程序、游戏及密码系统等等［1－3］。随机数发生器 （RNG）可分为伪随机数发生器 （PRNG）和真随机数发生器 （TRNG）两种［4－6］，伪随机数发生器又称确定性随机数发生器，它由一个确定的初始向量开始，通过一个确定的算法来产生随机数；真随机数发生器依托于自然界中物理现象的随机特性，如放射性衰变、电子电路的热噪声、散粒噪声等［7］。

真随机数因其具有随机性强、无周期和不可预测性，在密码系统和非密码系统中都有着广泛的应用，如彩票抽奖、模拟仿真、密钥生成和安全协议等。为此，设计基于硬件实现的真随机数发生器具有广阔的应用前景。本文利用RC电路充放电的低稳定度设计了一款真随机数发生器。

1 真随机数发生器的总体结构

为了提高随机序列的生成速率，本文采用8个噪声源模块 （N1－N8）并行工作，其总体结构如图1所示。

整个随机数发生器由8个噪声源模块、后处理模块、在线随机性检测模块、串行输出单元和并行输出单元组成。在随机数生成系统工作过程中，首先由8个噪声源模块连续不断地输出16位随机比特；然后通过后处理电路，经相应的后处理后，生成分布均匀、相对独立的随机序列；最后在线随机性检测模块对经后处理的随机序列进行实时检测，并根据检测结果进行报警和控制信号的输出。

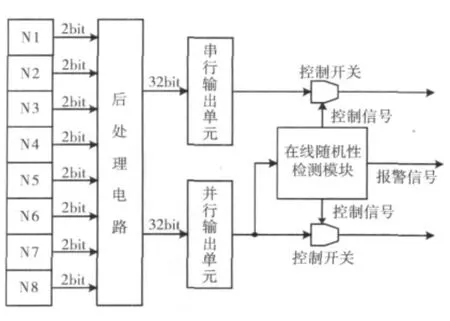
图1 TRNG结构框架

2 噪声源模块的设计

2.1 基本原理

在RC充放电电路中，由于受到环境温度、电压、电流、电阻热噪声等因素的影响，其充放电时间极不稳定。利用RC充放电的低稳定度特性作为真随机数发生源，收集数据，通过时钟周期量化器计数RC电路的充放电时间，获得不确定的2位二进制数据，其原理如图2所示。

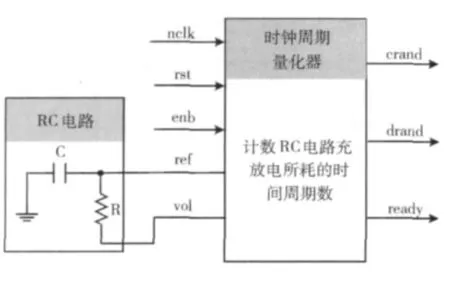
图2 噪声源实现原理

2.2 实现方法

2.2.1RC电路充放电过程

RC电路充放电策略是：vol作为RC电路电压配置端口，ref作为电容电压检测端口。当时钟周期量化器置vol为1时，该端口输出为高，输出电流通过电阻对电容进行充电；当时钟周期量化器置vol为0时，该端口输出为低，电容通过电阻进行放电。充放电过程如图3所示。

图3 RC电路充放电过程

2.2.2 时钟周期量化器

时钟周期量化器是一个数字电路模块，主要由一个充电计数器、一个放电计数器和一个控制状态机组成。充电计数器和放电计数器分别量化RC电路充电和放电所耗的时钟周期，控制状态机控制整个充放电过程，其工作流程如图4所示。

图4 时钟周期量化流程

当enb信号有效且经rst复位后，设置ready为0，并置vol为1开始对RC电路充电，当充电计数器检测到vol从0跳变为1时则开始计数并检测ref，当检测到ref为1时，表明充电结束；保存充电计数结果后复位充电计数器，设置vol为0，RC电路开始放电，当放电计数器检测到vol从1跳变为0则开始计数并检测ref，当检测到ref为0时，表明放电结束；保存放电计数器结果后复位放电计数器，置ready为1并输出充放电随机比特crand（charge random bit） 和drand（discharge random bit），其 中，crand和drand分别为充电计数器和放电计数器的最低比特位；直到检测到enb无效时则停止产生随机数，否则进行下一次充放电过程。

2.3 采样电路的设计

为从上述噪声源模块中采样得到随机的01序列，使得序列中0和1出现的概率尽可能地接近，本文基于非线性布尔函数，提出了一种有效的采样方法。

首先给出非线性函数的一个性质［8］：

定理1 设f是一个→F2的非线性函数，ε为f函数的输入向量中0和1的概率偏差，Δ（ε）为f函数的输出比特中0和1的概率偏差，则有

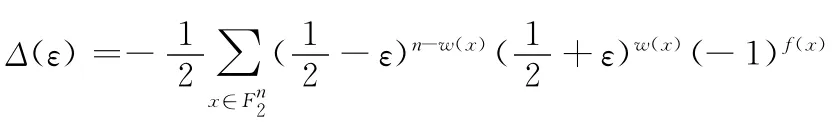
式中：w（x）——x的汉明重量。

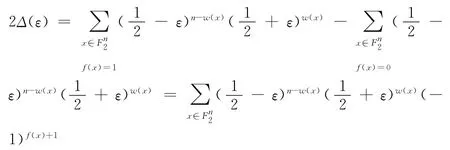
所以

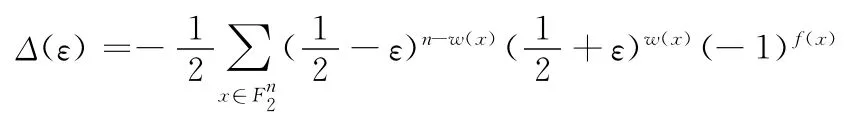
根据上述非线性布尔函数的性质，本文选择了一个易于硬件实现的二次非线性布尔函数，其表达式如下：f（x）＝f（x1，x2，x3）＝x2＋x3＋x1x2＋x2x3mod2，其真值表如表1所示。

表1 二次布尔函数的真值表

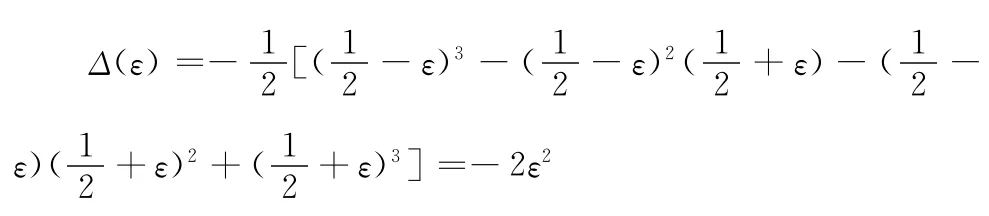
根据定理1可得

则有

图5给出了二次布尔函数的采样电路图，该电路结构简单，仅使用了3个D触发器、4个与门和1个异或门电路。在时钟clk的作用下，当ready信号为1时，使得EN有效，此时电路动作一次，完成一次采样，分别获得随机比特c和d。

3 后处理模块的设计

3.1 后处理算法

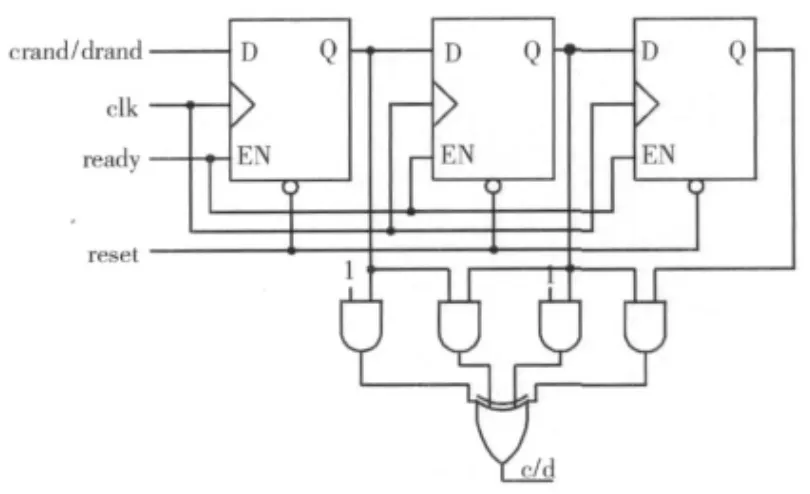
图5 基于布尔函数的采样电路

目前，常见的后处理算法有冯·诺依曼校正法［9］、级联的异或链法［10］、弹性函数［11－12］及哈希函数［13］等。前3种方法电路设计简单，易于实现；基于哈希函数的电路设计复杂，硬件实现代价相对较高。根据上述分析，本文基于模加、移位、异或、反馈等运算设计了一种新的后处理算法以生成等概、独立的随机序列。模加是一个有记忆变换模型，它可以将前几个时刻的计算结果存储下来，参与当前时刻的随机数生成，这使得当前时刻的随机数不仅与当前时刻输入的原始随机数有关，还与前几个时刻的计算结果有关。移位是算法中常用的运算，其电路通常以移位寄存器为基础设计的，主要包含逻辑移位和循环移位。异或有效地将两路不相干的输出序列进行了综合。反馈是指反馈移位寄存器的状态值不仅参与移位运算，其输出值还要反馈到输入端，参与其它函数运算。经过算法处理后，数字序列的均匀性、独立性及游程特性均得到改善，算法结构如图6所示。

图6 后处理算法结构

图6 给出了后处理算法的结构，其具体描述如下：

（1）符号定义

ci：8位采样编码，其为从8个噪声源采样得到的8比特c，其二元表示为

整个实践活动包括四个阶段，分别是：M+C(强调创意的构思)阶段、M+D(强调创新的设计)阶段、M+I(强调创造的实施)阶段、M+O(强调分享的运行)阶段，各个阶段的活动内容见表1。整个过程体现了体验教育、快乐教育、基于项目的教育和创造中学等教育理念。

di：8位采样编码，其为从8个噪声源采样得到的8比特d，其二元表示为

ri：8位移位编码，其二元表示为

si：8位移位编码，其二元表示为

ti：8位异或编码，其二元表示为

xi：8位加法编码，其二元表示为

yi：8位加法编码，其二元表示为

zi：8位加法编码，其二元表示为

k3～k0：4个8位并行移位寄存器，组成1组32位随机序列b31－0。

（2）运算符号描述

田：加法运算，表示两个8比特数据进行模256加；

⊕：异或运算，表示两个8比特数据进行逐位异或；

＜＜＜：循环左移运算，表示8比特数据循环左移1位；

＞＞＞：循环右移运算，表示8比特数据循环右移1位。

（3）算法流程

初始化：i＝0，s0＝r0＝0，kj＝0 （j＝0，1，2，3）；

1）i＝i＋1，采样得到ci，di；

重复1）～5），即可源源不断地产生随机数序列，其中连续采集4个ci和di后，生成一组32比特的随机序列b31～b0。

3.2 后处理电路

根据后处理算法的结构，结合后处理模块整体电路结构，采用数字电路设计技术，设计如图7所示的后处理单元电路。

从图7中可以看出，该电路主要由3个模加模块、两个循环移位模块、1个异或模块、两个8位D寄存器模块和8位宽的4级逻辑移位模块组成。它在采样时钟sclk的控制下完成相应的后处理操作。

图7 后处理单元电路

4 串并行输出单元的设计［14］

4.1 串行输出单元

在密码系统中，串行输出应用较少，但某些特殊的场合要求后处理单元输出的随机数序列是串行的，为此，在输出单元模块中设计了串行端口。其串行输出单元电路如图8所示。整个电路主要由1个5位二进制计数器和1个32位移位寄存器组成。在时钟clk的作用下，5位二进制计数器模块每32个时钟产生一个进位CO，当CO有效时，32位移位寄存器模块将输入数据逐位串行输出。

图8 串行输出单元电路结构

4.2 并行输出单元

目前，大多数密码系统要求真随机数发生器模块输出的随机数序列是并行的，这样方便其它模块对随机数的并行读取，本文设计了如图9所示的并行输出单元电路。

从图9可以看出，并行输出电路主要由八分频模块、2位二进制计数器模块、32位寄存器组成。首先，将时钟clk通过八分频模块得到采样时钟sclk；然后，在采样时钟sclk的控制下，2位二进制计数器模块每4个时钟产生一个有效的进位信号CO1，将32位随机数据输入到并行端口；最后，当读信号ren有效时，经与门输出后使得EN2有效，这时将32位数据并行输出；否则，并行输出控制使能信号EN2无效。

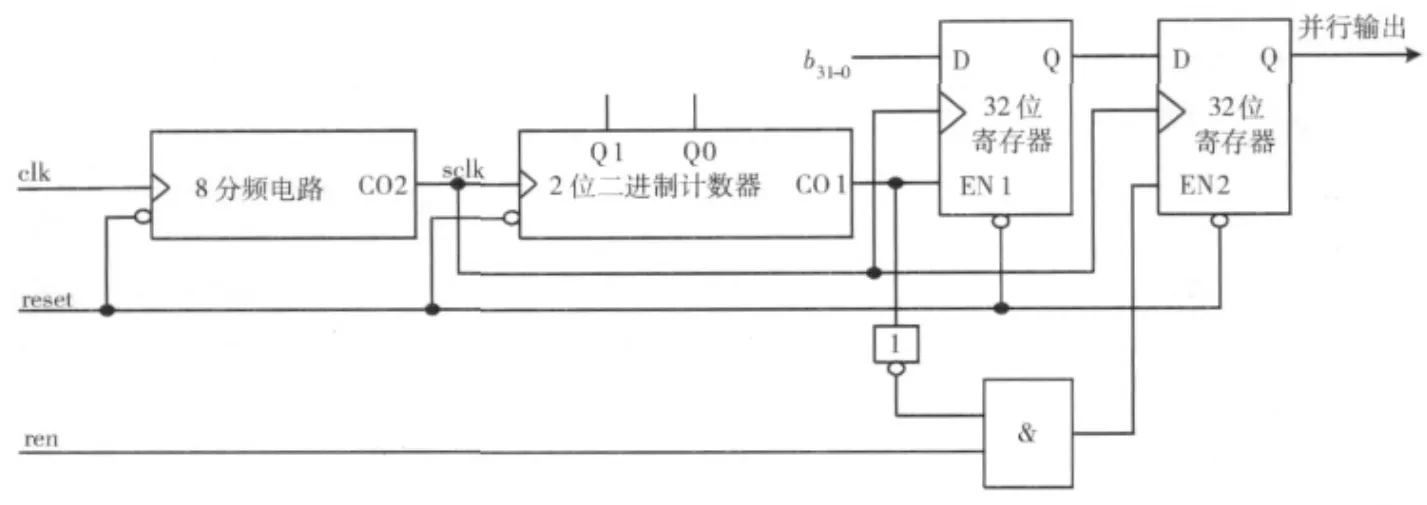
图9 并行输出单元电路结构

5 仿真与测试

根据整个真随机数发生器的结构框架，用Spectre模拟器对电路进行数模混合仿真，这里取量化时钟频率nclk＝100MHz，R＝1.69kΩ，C＝1.2nF，clk＝3.2MHz，sclk＝0.4MHz。通过实验采集20 000比特用于随机性检测，随机性检测遵循FIPS140－2标准［15］，进行频数检测、扑克检测、游程检测和长游程检测，检测结果如表2所示。

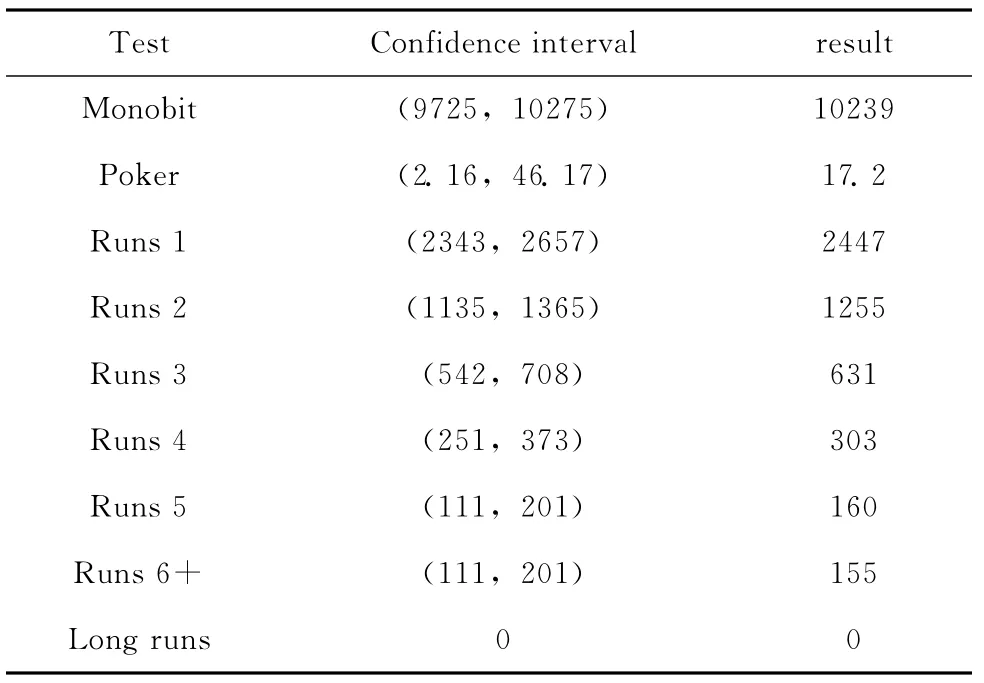
表2 FIPS140－2测试结果

测试结果表明，采用本文所提供方案产生的随机序列能够通过FIPS140－2的统计测试，具有良好的随机特性。

6 结束语

本文提出了一种数模混合的真随机数发生器，并完成了各个模块的设计与整个随机数发生器的仿真与测试。结果表明，随机数的生成速率为3.2MHz，且能够通过FIPS140－2的统计测试。该随机数发生器使用元件少，功耗低，稳定性高，在一些对随机数生成速率要求不高的场合有较大的应用意义。为满足信息安全系统对随机数高质量、高速率的要求，下一步的主要工作是设计高速、稳定、可靠的噪声源。

［1］GONG Hong.Design of true random number generator［D］.Guiyang：Guizhou University，2007 （in Chinese）.［龚红.真随机数发生器设计 ［D］.贵阳：贵州大学，2007.］

［2］Killmann，Schindler.A design for a physical RNG with robust entropy estimators［G］.LNCS 5154：Proceedings 10th International Workshop，2008：146－163.

［3］Dichtl M，Golic Dj.High speed true random number generation with logic gates only［G］.LNCS 4727：Proceedings of the 9th International Workshop on Cryptographic Hardware and Embedded Systems，2007：45－62.

［4］Werner Schindler.Random number generators for cryptographic applications［M］.Cryptographic Engineering，Springer，2009：5－23.

［5］Tsoi K H，Leung Ka Ho，Philip H W Leong.A high performance physical random number generator ［C］.IEEE Proc Computers ＆Digital Techniques，2007.

［6］Dries Schellekens，Bart Preneel，Ingrid Verbauwhede.FPGA vendor agnostic true random number generator ［C］.the Proceedings of the 16th International Conference on Field Programmable Logic and Applications，2007.

［7］ZHANG Wangcheng，WU Nanjian.A hybrid random number generator using single electron tunneling junctions and MOS transistors ［J］.Journal of Semiconductors，2008，29 （4）：693－700.

［8］Patrick Lacharme.Post－Processing functions for a biased physical random number generator［G］.LNCS 5086：15th International Workshop，2008：334－342.

［9］Michal Varchola.FPGA based true random number generators for embedded cryptographic applications ［C］.Proceedings of the 12th International Conference on Cryptographic Hardware and Embedded Systems，2010.

［10］ZHANG Xiaofeng，BAI Guoqiang，CHEN Hongyi.True random number generator for network security co－processor［J］.Computer Engineering，2009，35 （10）：229－231 （in Chinese）.［张晓峰，白国强，陈弘毅.应用于网络安全协处理器的真随机数产生器［J］.计算机工程，2009，35 （10）：229－231.］

［11］Sunar B，Martin W J，Stinson D R.A provably secure true random number generator with built－in tolerance to active attacks ［J］.IEEE Transactions on Computers，2007，56 （1）：109－119.

［12］HUO Wenjie，LIU Zhenglin，CHEN Yicheng，et al.Design of a true random number generator using FPGA ［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2009，37 （1）：73－76 （in Chinese）.［霍文捷，刘政林，陈毅成，等.一种基于FPGA的真随机数生成器的设计 ［J］.华中科技大学学报 （自然科学版），2009，37 （1）：73－76.］

［13］Berk，Sunar.True random number generators for cryptography ［M］.Cryptographic Engineering，Springer，2009：55－73.

［14］PAN Song，HUANG Jiye.EDA technology functional tutorial：VHDL edition［M］.4th ed.Beijing：Science Press，2010 （in Chinese）.［潘松，黄继业.EDA技术实用教程：VHDL版［M］.4版.北京：科学出版社，2010.］

［15］Santoro R，Sentieys O，Roy S.On－the fly evaluation of FPGA－based true random number generator ［C］.IEEE Computer Society Annual Symposium on VLSI，2009：55－60.