基于多方位分辨率图像的低频SAR地面运动目标检测方法
范崇祎 黄晓涛
(国防科学技术大学电子科学与工程学院 长沙 410073)
1 引言
低频合成孔径雷达(SAR)具有穿透叶簇或浅层地表进行成像的能力。因此,低频SAR系统应用于运动目标检测(GMTI)时,不仅能够检测裸露的运动目标,而且可以检测隐藏在叶簇下或伪装网下的运动目标。利用低频SAR实时成像系统还能够实现对运动目标的实时检测,具有较大的军事和民用价值。其中单通道的低频 SAR/GMTI系统成本低,易于工程实现。
与高波段SAR不同,低频SAR需要较大的方位积累角才能满足图像方位分辨率的要求。大积累角会导致静止杂波在方位谱上具有较宽的频谱,覆盖运动目标的频谱,难以应用基于多普勒频偏的运动目标检测算法[1,2]。大积累角所引入的长合成孔径时间则可能导致运动目标在雷达照射时间内产生严重的距离迁徙和跨距离单元,目标散焦严重,导致难以应用低阶的运动目标成像算法补偿运动目标的平移、散焦相位[3,4]。大积累角及长合成孔径时间还加剧了运动目标回波随入射角的变化,大大降低了运动目标的信杂比,影响检测性能。
目前,低频SAR单通道运动目标检测方法包括两大类:一类是通过更改成像参数,搜索运动目标的聚焦像[5,6],进而估计出运动目标的相对速度。这类方法考虑了运动目标的距离迁徙,需要对原始数据进行迭代成像,在同一像素点检测幅度峰值,从而估计运动参数。若运动目标所在区域未知,则计算量随着场景回波数据量的增加和测速精度的提高迅速增大,因此该类方法不适用于实时检测运动目标。第二类是利用运动目标在不同方位子孔径图像上的位置的变化信息,估计相对速度[7-9]。这类方法易于实现,计算量小。但低频SAR中,运动目标的回波信号随入射角变化剧烈,导致在某些子孔径图像上难以检测到运动目标像的幅度。当图像中的杂波能量很强时,运动目标的散焦像极易受到杂波旁瓣的影响,无法检测图像序列上的位置,难以通过变化检测估计速度参数。
低频 SAR单通道运动目标检测方法在处理过程中难以避免生成运动目标的散焦像。散焦像包括运动目标的模糊与散焦。其中模糊是指匹配滤波器不完全匹配时一阶相位误差引起的变化,通常指目标距离迁徙导致的距离向偏离,即跨距离单元;散焦是指由于匹配滤波器不完全匹配时二阶相位误差引起的变化,通常指方位向调频斜率误差导致的主瓣展宽[10]。虽然散焦像信噪较低,存在模糊与平移,通常作为检测过程中的多余信息被去除,但它包含了运动目标在合成孔径时间内的运动信息,不同速度的运动目标具有不同的散焦像。现有方法仅对聚焦像和散焦像的位置进行了研究,没有充分研究散焦像的形状及其能量变化所包含的运动信息。本文基于低频SAR高方位分辨率图像,构造不同方位分辨率图像。根据运动目标散焦像的变化特点,提出了一种能够迅速检测低频SAR运动目标的方法。所提方法克服了运动目标回波随入射角的变化,并且计算量小,适合实时进行运动目标检测。本文结构如下,第 2节基于非线性频调变标(NCS)算法,推导了运动目标的散焦像,给出了不同方位分辨率下散焦像的形状变化。第3节进一步推导了散焦像的能量变化规律,对多方位分辨率图像中静止目标像与运动目标的散焦像进行了对比分析。基于该规律,第4节设计了基于多方位分辨率图像的低频SAR运动目标检测方法,并给出了算法的实现流程。第 5节通过仿真与实测数据验证了该方法的有效性。最后,总结全文。
2 运动目标的散焦像




对式(2)中的耦合相位作关于fr的泰勒级数展开,并保留到二次展开项。然后,对近似后的回波信号作距离 IFFT变换,则得到距离多普勒域回波信号


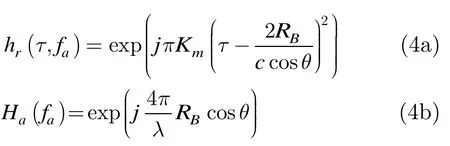
距离迁徙误差ΔR将导致散焦像发生弯曲,ΔR描述了不同斜视角下距离迁徙曲线的误差,其绝对值的最大值对应了运动目标散焦像的距离模糊,影响了散焦像的峰值位置。注意到式(3)中方位向窗函数不仅定义了合成孔径时间所对应的积累角长度,而且定义了积累角中心,即运动目标径向速度vr引起的多普勒偏移。因此,ΔR不仅与相对速度V有关,还与径向速度vr有关,可以用来区分运动目标的2维速度,克服了单通道SAR系统难以检测相同相对速度的运动目标的问题[11]。仿真发现,方位分辨率越高,相对速度越大,运动目标产生的距离模糊越大。同一相对速度下,径向速度vr产生的多普勒频偏还会加剧距离模糊。
3 多方位分辨率图像中目标像的能量变化
虽然低频 SAR中运动目标散焦像具有明显的形状特征,但是在实际的运动目标检测中,运动目标形状特征易受杂波分布及散射特性的影响,因此不能直接作为评价的依据。考虑场景中同一斜距处具有相同散射特性的静止点目标与运动点目标。方位分辨率越高,成像积累角越大,合成孔径时间越长,二者的总能量越大。静止点目标随着方位分辨率的提高,聚焦像的能量增加[12],所占的主瓣宽度减小。而运动目标散焦像会随着方位分辨率的提高,产生距离模糊与方位向散焦,运动点目标的能量会因为运动速度呈现不同的变化特征。
令Fi(i= 0 ,1,… ,N)表示方位分辨率ρi下获得了的图像序列。设静止目标和运动目标的能量均为Ei,则有Ei=αiE0,αi为常系数,E0为高分辨率ρ0时静止目标的能量。实际处理中,每幅图像的幅度均进行了归一化处理,归一化系数包含在常系数αi中。因此,方位分辨为ρi时对应的静止目标主瓣内像素单元的归一化能量为

同样地,运动目标主瓣内像素单元的归一化能量为

Psi与Pmi分别为静止目标与运动目标主瓣 3 dB宽度占据的像素数,代表了目标的形状。图像Fi与图像F0中的静止目标主瓣内对应像素单元的归一化能量比为

理想情况下,随着图像方位分辨率的降低,静止目标的形状有规律地扩大。而图像Fi与图像F0中的运动目标主瓣内对应像素单元的归一化能量比为

运动目标的形状变化与运动速度有关。zs与zm利用每个像素的幅度值,反映了多方位分辨图像上聚焦像与散焦像的形状变化。

图1 不同速度目标归一化能量随方位分辨率的变化
由第2节分析可知,运动目标方位向调频斜率误差引起的散焦像展宽远大于距离向二次压缩调频斜率误差的影响。通过基于式(3),式(4)的仿真,图1(a)给出了不同方位向速度目标归一化能量e随方位分辨率ρi变化的理论值,此时Pmi仅与方位向速度有关。随着方位分辨率的降低,静止目标的归一化能量逐渐降低,而运动目标的归一化能量有所增加。相对速度越大,变化越明显。含有方位向速度的运动目标存在理想的方位分辨率,使得在该方位分辨率下,运动目标的归一化能量相对较高。图1(b)给出了归一化能量变化的仿真结果。仿真包括了多种速度的运动目标高方位分辨下的散焦像。其中,仅具有方位向速度的运动目标的归一化能量变化与图1(a)的变化趋势相同。当目标距离向速度较小时,平均能量的变化趋势与静止目标相近;当距离向速度较大时,距离模糊严重,归一化能量较弱。
4 基于散焦像的快速检测
根据多方位分辨图像上目标的变化规律,本文提出了一种基于低频 SAR多方位分辨率图像的运动目标检测方法。该方法的基本思想为:根据理想静止目标在不同方位分辨率图像的变化,构造基于高方位分辨率图像的滤波器,使得静止目标在多方位分辨率图像中得到对消。然后,通过多方位分辨图像的变化迅速检测出运动目标可能存在的位置。所提方法的具体实现流程为:
步骤 1 图像获取 通过方位频谱的低通滤波器获得不同方位分辨率的图像。多方位分辨率图像可通过回波数据或低频 SAR的高分辨图像的方位频谱滤波获取。文献[7]的研究表明,无论是对回波数据还是对高分辨图像低通滤波效果是相同的。为了便于检测,在低通滤波时需要对其进行补零,使得不同方位分辨率的图像具有相同的像素点。同时,对不同分辨率图像幅度进行归一化。
步骤 2 邻域滤波 设计邻域滤波器消除静止目标在不同方位分辨率下的图像差异。高方位分辨率图像获得了更多静止杂波的细节。当多个理想静止点目标邻近时,随着方位分辨率的提高,目标的成像中心会发生分裂。根据点散射中心理论,低分辨图像中每个分辨单元内的能量可以看作高分辨图像中相对应的多个分辨单元的能量和。为了减小高方位分辨率下邻近静止目标的分裂,增强运动目标的变化特征,需要对高分辨图像进行邻域滤波。邻域滤波以低方位分辨率图像FN(x,y)为参照,利用高方位分辨图像Fi中的强杂波点设计滤波器,使得经过邻域滤波获得的高方位分辨图像与FN(x,y)的强杂波目标能够对消。再将该邻域滤波器应用到方位分辨率图像,获得邻域滤波后的图像i(x,y)。邻域滤波降低了高方位分辨率图像的分辨率,抑制了静止目标在图像上的分裂,同时保留了运动目标散焦像的形状。根据仿真,虽然运动目标散焦像的距离向IRW展宽比和方位向的展宽比变化趋势相同,但远不如其变化明显,在检测时可以只考虑方位向IRW展宽比随方位向分辨率的变化。因此邻域滤波器可以使用一维滤波器,如中值滤波器、三角窗函数等。滤波器宽度取决于低方位分辨率图像上典型点目标的宽度。

步骤 4 似然比与形状检测 利用多方位分辨率图像上静止与运动目标能量差异,构造似然比检测。

其中常数0<ε≪1,γ为门限,其值由运动目标的信杂比确定。似然比检测结果反映了包括静止杂波、噪声及运动目标的方位向能量特性。由于图像的动态范围较大,检测结果受到的干扰较多,需要对检测后的图像进行简单的聚类[12],判断目标分布的形状,通过形状检测有效排除杂波与噪声的干扰,判断运动目标的位置。
图2(a) 给出了仿真的高方位分辨率图像。其中中心斜距为556 m,其它参数与表1相同。图像中标号1~标号10为不同速度的运动目标和标号11~标号 14为静止目标,各目标信息如表 2所示。图2(b)~2(f)给出了步骤1~步骤4的结果。图2(b)给出了根据步骤1进行频谱滤波获得的低方位分辨率图像。该图像提高了具有方位向速度的运动目标的聚焦质量,使得运动目标在低分辨率图像上具有相对较高的信杂比,易于检测。以该图为参照,设计了一维三角窗函数,对高方位分辨率图像进行步骤2的邻域滤波,结果如图2(c) 所示。邻域滤波保留了运动目标在高方位分辨率图像上的形状特征。 根据步骤3,对图2(b), 2(c)分别进行相关计算,获得低方位分辨率的待检测图像,即图2(d)和图2(e)。待检测图提取了运动目标的主要特征,同时降低了静止目标在不同方位分辨率图像上的差异。利用待检测图像进行步骤4操作,获得的似然比与形状检测结果如图 2(f)所示。似然检测的结果表明:经过邻域滤波等操作后,静止目标在不同方位分辨率下的单位像素归一化能量变化远小于运动目标的变化,其中具有方位向速度和较大距离向速度的运动目标变化相对更大。
图2(f) 表明该方法能迅速检测出不同速度的运动目标。在检测出运动目标的位置后,即可以采用多种手段估计运动目标的各项参数。当信噪比足够高时,可以直接利用多方位分辨率图像的运动像进行序列分析,估计运动参数。根据步骤4的检测结果,拟合方位向IRW和ΔR的变化曲线lIRW,lΔR,判断运动目标速度。

表1 低频SAR系统参数

图2 基于散焦像的快速检测结果
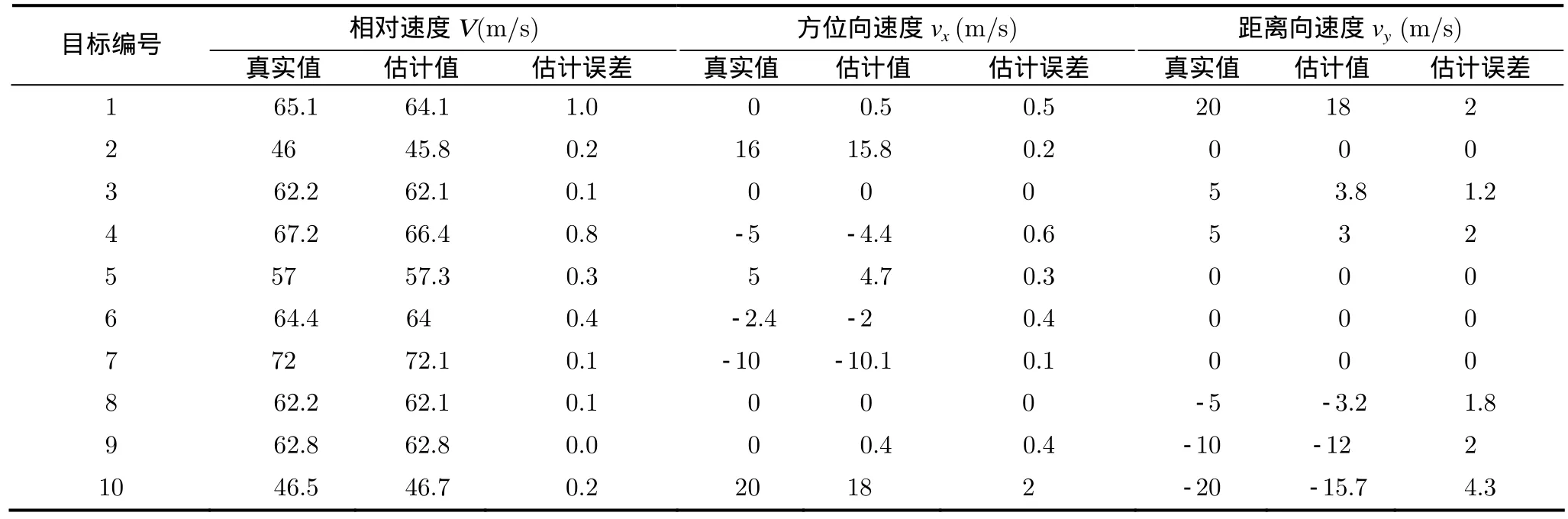
表2 低频SAR系统仿真的目标参数
5 数据验证
5.1 实测数据
利用单通道低频SAR接收的实测数据,对本文所提方法进行验证,系统参数如表1所示。地面合作目标在道路上以40 km/h的速度远离雷达航线行驶。道路两侧有较高大的建筑物,杂波能量相对较强。在高方位分辨率图像上,运动目标的信杂比为-45 dB。图3(a)给出了对1 m方位分辨率图像进行1维邻域滤波后的图像,该图在一定程度上消除了高分辨图像上静止目标的分裂现象。根据步骤 3,判断高低方位分辨率图像上各条方位线上的多个峰值位置,计算单位像素能量,再根据步骤 4,计算所获待检测图像的似然比。图 3(b)给出了似然比计算的局部图,该图像上静止杂波具有类似的单位像素能量分布,而运动目标具有不同的分布特征。经过幅度和形状检测后,存在运动目标的区域较为明显,如图3(c)所示。
根据检测结果,图4(a)~4(b)给出了高/低方位分辨率下运动目标的散焦像。由于运动目标的信杂比较低,反射特性随方位角变化较大。根据检测出的目标散焦模糊像的变化规律,可发现运动目标形状基本对称,距离向速度在0附近;估计的方位向速度区间为[-14 m/s, -10 m/s]。结合搜索聚焦像检测运动目标的方法,最终得到了运动目标速度的精确估计vx=-1 2.5m/s,vy= 0 m/s,如图 4(c)所示。
5.2 性能评估
利用仿真数据的检测结果(图2(f))进一步估计各个运动目标的运动参数,如表2所示。由表2可发现,目标2与目标10具有相同的相对速度V,不同的方位向速度和距离向速度。由于考虑了方位向窗函数的加权,能够利用单通道数据区分运动目标的2维速度。
由表2可发现,在信噪比较高的情况下,本文所提方法能够较准确地估计出运动目标的相对速度,检测方位向速度的性能优于距离向速度。在低频SAR信噪比较高的情况下,能检测的最小相对速度达到了0.2 m/s,能检测的最大相对速度取决于杂波谱宽度。检测过程中,对不同速度的运动目标尤其是具有较大距离向速度的运动目标,选择合适的低方位向分辨率,有助于检测性能的提高。改变运动目标的信噪比,对多种不同速度的运动目标进行多次检测,统计检测概率。如图5所示,实验中的虚警概率设为 1 0-3。其中图5(a)中统计的运动目标仅存在方位向速度,图5(b)中统计的运动目标均具有10 m/s的距离向速度。图5表明,信噪比的增加会提高该方法的检测性能。该方法对方位向速度比距离向速度敏感,对具有方位向速度的运动目标的检测概率相对较高。
6 总结
本文提出了一种适用于低频 SAR的运动目标检测算法,能够快速检测被杂波谱覆盖的运动目标。通过分析运动目标的成像原理,研究了运动目标在不同方位分辨率下散焦像的变化特点,并利用方位向3 dB宽度、距离模糊长度和归一化能量给出了运动目标散焦像的变化规律。基于上述分析,提出了基于多方位分辨率图像运动目标散焦像的检测方法。仿真与实测数据表明:该方法能够迅速检测出运动目标,尤其是具有方位向速度分量的运动目标。所提方法具有计算量小,信噪比要求低,能够克服运动目标反射系数随方位角的变化,速度检测范围大等优点。实验结果表明该方法具有较好的实用性。

图3 ROI区域检测

图4 不同方位分辨率下的运动目标ROI区域

图5 不同信噪比下的检测概率
[1]Raney R K. Synthetic aperture imaging radar and moving targets[J].IEEE Transcations on Aerospace Electronic System, 1971, 7(5): 499-505.
[2]Chen H C and Mcgillm C D. Target motion compensation by spectrum shifting in synthetic aperture radar[J].IEEE Transcations on Aerospace Electronic System, 1992, 28(3):895-901.
[3]蔚婧, 廖桂生. 一种多通道运动目标重聚焦及运动参数估计方法[J]. 西安电子科技大学学报, 2009, 36(4): 624-628.
Yu Jing and Liao Gui-sheng. Multi-channel moving target focusing and parameter estimation algorithm[J].Journal of Xidian University, 2009, 36(4): 624-628.
[4]Dias J and Marques P. Multiple moving target detection and trajectory parameters estimation using a single SAR sensor[J].IEEE Transcations on Aerospace Electronic System, 2003,39(2): 604-624.
[5]Sjögren T K, Vu V T, and Pettersson M I. Moving target detection by focusing for frequency domain algorithms in UWB low frequency SAR[C]. IGARSS 2008, Boston, MA,USA, July 7-11, 2008: I-161-I-164.
[6]Vu V T, Sjögren T K, Pettersson M I,et al.. Detection of moving targets by focusing in UWB SAR-theory and experimental results[J].IEEE Transcations on Geoscience Remote Senssing, 2010, 48(10): 3799-3815.
[7]周红, 黄晓涛, 常玉林, 等. 基于三通道UWB SAR子孔径图像序列的ATI方法[J]. 电子学报, 2009, 37(5): 930-936.
Zhou Hong, Huang Xiao-tao, Chang Yu-lin,et al.. Along track interferometry method based on sub-aperture image series for triple—channel UWB SAR[J].Acta Electronica Sinica, 2009, 37(5): 930-936.
[8]周红, 黄晓涛, 常玉林, 等. 子带子孔径ATI地面运动目标检测及参数估计方法[J]. 电子与信息学报, 2010, 32(1): 62-68.
Zhou Hong, Huang Xiao-tao, Chang Yu-lin,et al.. A ground moving target detection and parameter estimation method using subband and subaperture along track interferometry[J].Journal of Electronics&Information Technology, 2010, 32(1):62-68.
[9]常玉林, 黄晓涛, 周红, 等. 运动目标在阵列孔径UWB SAR图像上的表征及其在图像域GMTI方法中的应用[J]. 宇航学报, 2009, 30(3): 1146-1153.
Chang Yu-lin, Huang Xiao-tao, Zhou Hong,et al.. The representation of moving targets in multi-channel UWB SAR images and it’s application in image domain GMTI methods[J].Journal of Astronautics, 2009, 30(3): 1146-1153.
[10]Cumming I G and Wong F H. Digital processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M].Norwood, MA, USA, Artech House Inc, 2005: 64-67,117-124.
[11]Chapman R D, Hawes C M, and Nord M E. Target motion ambiguities in single-aperture synthetic aperture radar[J].IEEE Transcations on Aerospace Electronic System, 2010,46(1): 459-468.
[12]孙吉祥, 等. 现代模式识别[M]. 长沙: 国防科技大学出版社,2001: 13-43.

