异构网中宏、微基站间存在频偏时的干扰协调方法

凌 为 韩圣千 徐志昆 杨晨阳

(北京航空航天大学电子信息工程学院 北京 100191)

1 引言

近年来，异构网受到了学术和工业界的广泛关注。通过在宏(macro)基站的覆盖范围内增加一些低功率节点，例如微(micro)基站、毫微(pico)基站、家庭基站(femtocell)、远程射频节点(RemoteRadio Head, RRH)和中继(本文将这些节点统称为微基站)，可以增强对热点地区的覆盖，从而有效地提高整个蜂窝网络的吞吐量[1]。

与同构网相比，微基站的引入使得干扰环境更为复杂，因此对异构网中的干扰进行协调是目前的研究热点之一。目前提出的干扰协调技术主要集中在频谱划分和功率控制方面。3GPP的提案[2]总结了通过在时域设置空白帧以及通过功率控制进行干扰协调的方法。这两种方法在实际系统中简单易行，但是不能充分挖掘异构网的潜在性能。文献[3, 4]研究了采用分数频率复用(Fractional Frequency Reuse, FFR)进行干扰协调的方法，通过调整小区频率复用因子来协调宏、微基站间的干扰。文献[5]把系统的工作带宽划分成多个子频带，然后采用与文献[3, 4]中类似的 FFR方法，动态地选择微基站的工作子频带，并进一步对子频带进行功率分配来实现对宏用户的干扰抑制。但是，由于采用了FFR，文献[3-5]的方法降低了整个网络的频谱利用率。文献[6,7]利用功率控制来对异构网中的干扰进行协调，所提出方法的性能优于简单的干扰回避[2]。最近，3GPP提出了一种针对异构网的协作多点传输场景，在宏基站和RRH 间进行协作[8]，这要求两类基站之间存在高容量、低延迟的骨干网。

本文考虑骨干网只能进行少量信息交换的异构蜂窝网络，研究多载波微基站系统进行下行传输时对宏用户的干扰协调问题，设计把对宏用户的干扰控制在允许范围内时使微基站性能最优的收发算法。在这种场景下，宏基站和微基站之间会存在频偏，与传统OFDMA系统内收发机之间的频偏不同，这种系统间的频偏带来的影响不能用现有的频偏校正方法解决。文献[9]的研究结果表明，若不考虑频偏的影响，则对主次系统的干扰协调性能将急剧下降。本文将考虑宏基站和微基站之间存在的频偏，在把对宏用户的干扰控制在某个干扰门限以内的前提下，以使微基站数据率最大为目标，设计低复杂度发射预编码。所提出的方法只需要宏基站和微基站通过骨干网交换少量信息，具有较低的信息共享资源开销。

2 系统模型

本文所采用的数学符号定义如下：E[·], [·]m,n,Tr(·), ( ·)-1, ( ·)T, ( ·)*和 (· )H分别代表求期望、矩阵中第m行第n列的元素、求迹、求逆、求转置、求共轭和求共轭转置，IN代表N×N维单位阵，1N代表N×1维全 1列向量， d iag{a1,… ,aN}代表第n个对角元素为an的对角阵。

考虑一个全频复用的异构网络，如图1所示，其中包含一个宏基站和一个微基站。宏基站和微基站均以OFDMA方式服务其各自的多个用户，且为了简单我们只考虑同一时隙里微基站只服务一个微用户。本文考虑下行传输时宏基站和微基站之间的干扰协调。我们首先考虑一个宏用户位于微基站附近、且其子频带落入微用户子频带内的情况，而后再讨论有多个宏用户位于微基站附近的情况。

图1 下行传输时异构网拓扑图

假设宏基站和微基站系统的载波间隔相同。微用户所占用的载波数为Ns，受干扰的宏用户所占的载波数为Np(Np≤Ns)，不失一般性地，设宏用户所占载波集合为G= { 1,…,Np}。假设宏基站、宏用户、微基站和微用户均采用单天线，并且宏基站与宏用户、微基站与微用户之间通过一些传统的方法分别进行时频同步。但是，宏基站和微基站之间存在着df的频偏且无法通过现有方法进行校正，该频偏信息可以通过微基站侦听宏用户发送的上行训练序列等方式进行估计。

2.1微基站的信号模型

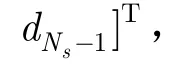
其中B为频域预编码矩阵，xf=Bd为经过预处理后的频域信号，F为Ns维DFT转换矩阵。

设系统采用足够长的循环前缀，从而可以消除多径信道带来符号间干扰，则微用户的时域接收信号为

其中Hss是微基站到微用户的时域信道矩阵，是一个Ns×Ns的循环移位矩阵，其第1列为微基站到微用户的信道脉冲响应hss=[hss( 0),…,hss(Lss-1),0,…,0]T,Lss为微基站到微用户的多径条数，n为微用户接收机的加性白高斯噪声，um为微用户收到的来自宏基站的干扰，z=um+ni是均值为0，方差为的等效噪声。

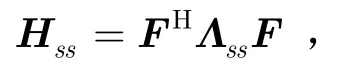
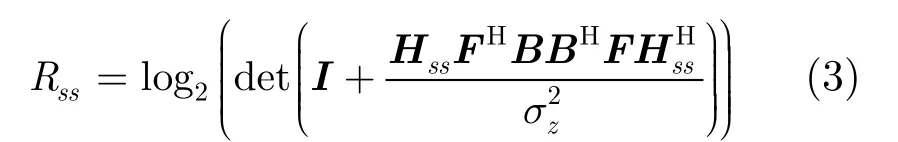
2.2 宏用户的信号模型

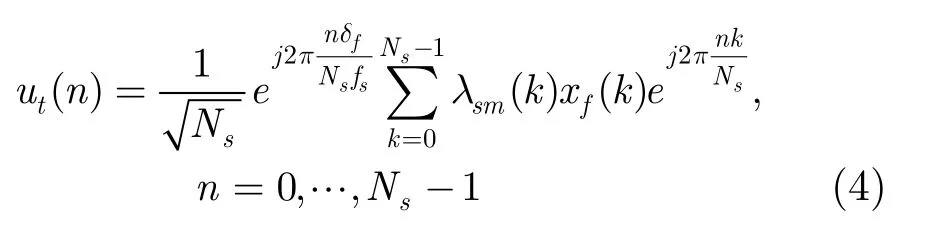
其中xf(k)为xf的第k个元素，lsm(k)为微基站到宏用户在第k个载波上的频域信道响应，fs为载波间隔。

由于xf=Bd和Λsm=FHsmFH，宏用户在时域接收的干扰信号向量可以表示为

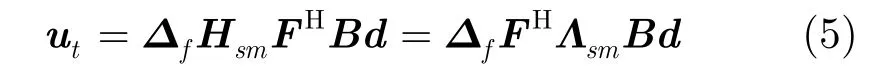
在第k个载波上宏用户收到的来自微基站的频域干扰信号为

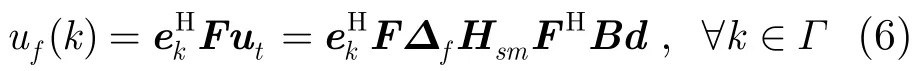
其中ek表示在第k位为1，其他位为0的列向量。

宏用户在第k个载波上的接收信号为

其中s(k)为在第k个载波上宏基站发送给宏用户的信号，lmm(k)为宏基站到宏用户在第k个载波上的频域信道响应，(k)为宏用户接收机的均值为 0，方差为的等效加性白高斯噪声。

为了保证宏用户的性能，需要限制微基站对宏用户造成的干扰功率不超过某个干扰门限。本文采用文献[11]提出的准则来计算干扰门限，即在存在微基站的干扰时，宏用户的归一化性能下降比率不超过某一个预设的值。所允许的最大干扰功率(即干扰门限)为

其中S(k) = |lmm(k)|2是来自宏基站的信号功率，I(k) = Ed[ |uf(k)|2]是微基站到宏用户的干扰功率。计算上述干扰门限需要知道S(k)和。这两个信息可通过宏用户向宏基站反馈得到，宏基站再将计算得到的干扰门限通过骨干网传给微基站进行干扰协调。

3 微基站对宏用户的干扰协调

本节将设计能够在保证宏用户性能的前提下最大化微用户可达数据率的发射预编码方法首先对最优预编码的设计问题进行建模，为了降低最优方法的复杂度，将提出一种次优的预编码设计方法。本节首先针对已知瞬时干扰信道信息的情况进行设计，而后将结果推广到已知统计干扰信道信息的情况；还将分析有多个宏用户时所提出方法的可扩展性，最后分析比较最优方法和次优方法的计算复杂度。

3.1 最优预编码

为了保证宏用户的性能，微基站到宏用户的干扰功率不能超过干扰门限。假设已知微基站到宏用户的瞬时干扰信道，则 Ed[|uf(k)|2]为微基站到宏用户的平均干扰功率，其干扰约束可以表示为

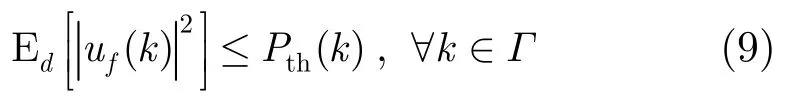
定义ck=FHek,Bt=FHB并把式(6)代入式(9)，则干扰约束表达式可化简为

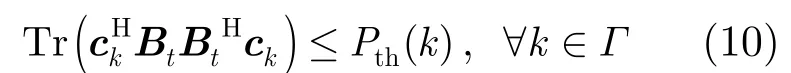
在考虑微基站的发射功率约束和对宏用户的干扰功率约束式(10)后，使微用户的可达数据率最大的优化问题可以建模为

定义Θ=B BH，则优化问题式(11)的优化目

3.2 低复杂度次优预编码

当载波数较多时，以上的最优方法复杂度很高。下面，将提出一种次优的低复杂度预编码设计方法。

由于有了式(10)所示的干扰约束，优化问题式(11)不再是一个典型的多输入多输出(Multiple Input Multiple Output, MIMO)系统的容量最大化问题，因而其最优预编码没有显式解。为了降低复杂度，我们将预编码拆分为两部分，并通过限制这两部分的结构来对约束条件式(10)进行松弛，进而提出一种基于迭代的次优方法。这种迭代方法在每次迭代过程中都能得到显式解，因此具有较低的复杂度。

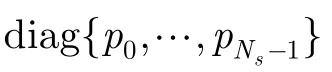
我们进一步将B*分为两部分进行设计：

其中B2将被设计为使微基站的下行信号不对宏用户造成干扰的预处理矩阵，即B2处于等效干扰信道的零空间上，∀k∈G。它需要满足如下条件：

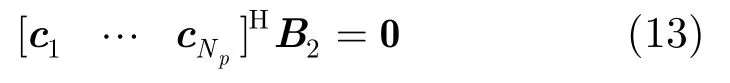
定义矩阵Φ=[c1…]H,N2为Φ的非零奇异值的个数，K,Q分别为Φ右奇异矩阵的前N2列和后Ns-N2列。则K,Q分别在Φ的正交零空间和零空间上。根据式(13)，以及B*为酉阵B1,B2具有如下的结构：

其中V1为一个N2×N2维的酉阵，V2为一个(Ns-N2)×(Ns-N2)维的酉阵。

将式(14)，式(15)和式(12)代入原来的优化问题式(11)中，化简后可以得到如下新的优化问题：

这个优化问题是关于(V1,P1,V2,P2)的凸问题，但仍然没有显式解。下面提出一种迭代求解(V1,P1)和(V2,P2)的方法，通过使每次迭代过程有显示解来达到降低复杂度的目的。

首先，给定(V2,P2)，并将其代入式(16)的目标函数中，则

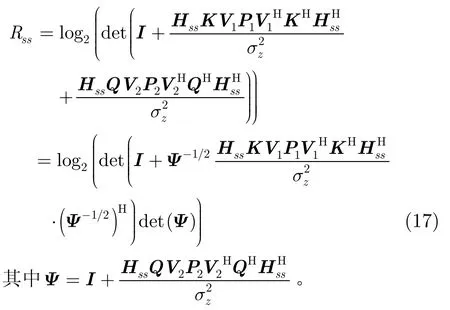
此时，优化问题式(16)退化为以(V1,P1)为变量的凸问题，如下所示：

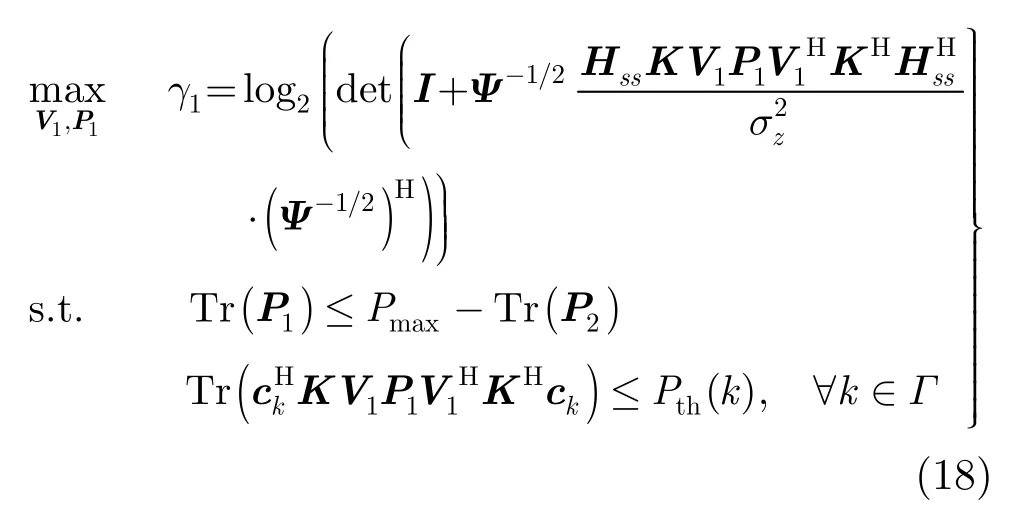
优化问题式(18)的最优解仍没有显示解。不过，如果忽略式(18)中的第 2个约束条件，不难发现该优化问题退化为MIMO系统容量最大问题，相应的最优预编码V1为等效信道1=Ψ-1/2Hss K的右奇异矩阵。将这样得到的V1代入式(18)中，通过推导(推导过程略)，可以得到P1的优化问题为

其中p1(k)为P1的第k个对角线元素，p1为P1所有对角线元素组成的列向量，r(k)为等效信干噪比，A为功率约束矩阵。

求解最优的p1是一个典型的多水平面灌水问题，根据卡罗恩-库恩-塔克条件(Karush–Kuhn–Tucker, KKT)条件[13]可以得到如下的最优功率分配：

其中(x)+= max(x,0),β= (β1…β1+Np)T为满足式(19)中约束的水平面向量。

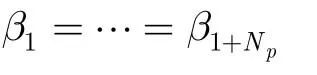
其次，在给定(V1,P1)时求解(V2,P2)。将已知的(V1,P1)代入式(16)中，并通过与得到式(17)时类似的推导，得到与式(18)类似的优化问题建模：

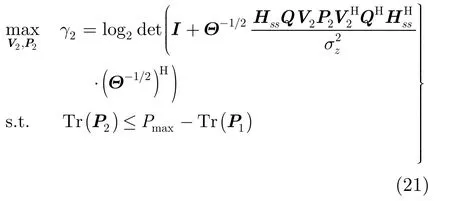
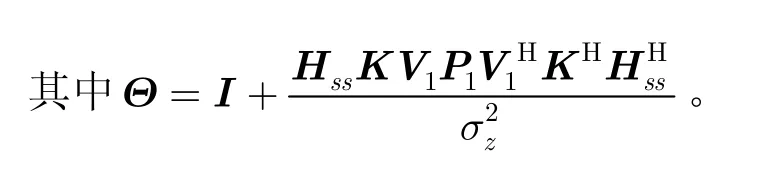
不难发现，此优化问题是一个典型的MIMO系统的容量最大化问题，其最优发射预编码有显式解：V2为等效信道2=Θ-1/2Hss Q的右奇异矩阵，P2为通过单水平面注水得到的功率分配矩阵。

这样，我们就完成了一次迭代过程：在已知(V2,P2)时，求解得到次优的(V1,P1)；在已知(V1,P1)时，求解得到最优的(V2,P2)；这两部分都有显示解。将式(14)，式(15)代入式(12)中，可以求得微基站的发射预编码Bt，并且这个过程可以循环迭代下去。

值得一提的是，当NP=Ns时，也即宏用户所占载波数等于微用户所占载波数时，N2等于0，不存在与等效干扰信道正交的B2，此时B=B1P1，无需迭代。从后面的仿真结果可见，本文所提出的次优方法迭代一次就可以获得良好的性能。

3.3 推广：多个宏用户的情况

此时，同样可以采用式(8)计算干扰门限。根据不同宏用户反馈的信号功率S(k)和等效噪声功率，宏基站计算得出第i个宏用户的干扰门限(k),k∈Gi。

3.4 已知统计干扰信道时的干扰协调

如果微基站不能获得瞬时干扰信道信息，而只能获得统计干扰信道信息，前面所提出的方法同样适用，只是在已知统计干扰信道信息时，等效的干扰信道会发生变化。

若已知干扰信道的协方差矩阵，在求干扰功率的期望时，与式(9)不同，需要对发射数据d和干扰信道hsm同时取期望， 此时干扰约束式(9)经过化简可以得到

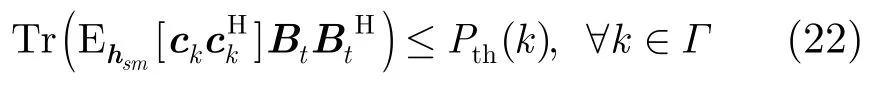
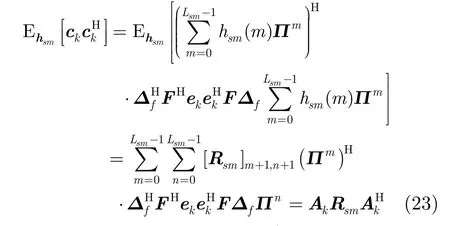
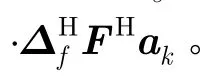
综合式(22)和式(23)，再经过矩阵变换，则微基站对宏用户的干扰约束可以表示为

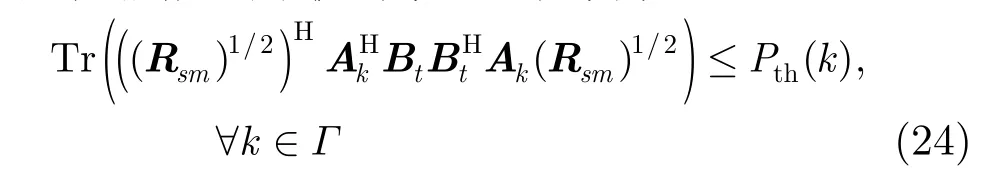
比较式(24)和式(10)，不难发现在已知统计干扰信道时，只需要用Ak(Rsm)1/2代替已知瞬时干扰信道时的ck，因此前面所提出的最优和次优方法仍然适用。

3.5 复杂度分析

下面分析所提出的次优预编码的计算复杂度。该次优方法要对Φ,1和2进行奇异值分解，其计算复杂度均为O(NslogNs)[14]；要对Ψ和Θ进行矩阵求逆，其复杂度为O(Ns3)[15]；还要在求解P1,P2时采用单水平面注水功率分配算法，其复杂度比矩阵求逆要低很多，这里忽略不计。因此，所提出的次优方法每迭代一次的计算复杂度为O(Ns3)。例如，若系统中总载波数为64，求解最优发射预编码时的精确度e= 0 .01，则次优方法计算复杂度为O(6 43)，与最优算法的复杂度O(2 × 6 46.5)相比降低了百万倍的量级。

4 仿真结果及分析

本节通过仿真评估所提出方法的性能。表1是部分仿真参数，其中宏用户和微用户均分布在宏基站和微基站的连线上。

图2给出了所提出迭代次优方法的收敛性，其中Ns= 6 4，宏基站到宏用户、微基站到微用户、微基站到宏用户的多径条数分别为2、6和4。图中上下两部分是宏用户所占载波数分别为16和48的情况，从左到右宏用户所允许的性能下降比率分别为0.05、0.1，宏基站与微基站之间的归一化频偏为0.3，并且考虑已知瞬时干扰信道信息。从仿真结果可见，所提出的次优方法只需迭代一次就可以获得很好的性能。已知统计干扰信道信息时的仿真结果与此类似，由于篇幅限制，这里不再给出结果。

表1 仿真参数

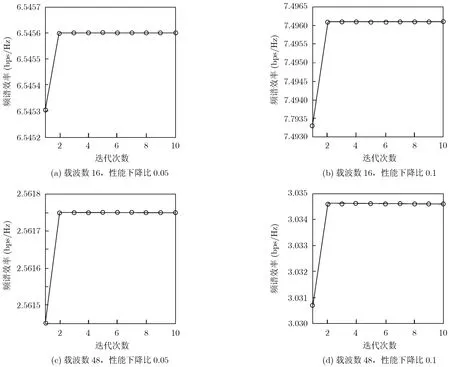
图2 次优迭代方法的收敛性

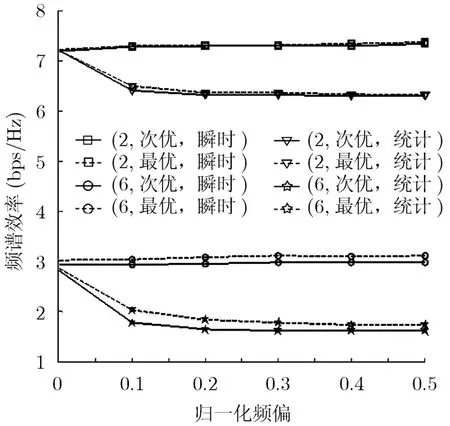
图3 采用最优预编码和次优预编码时微用户的频谱效率

图3给出了已知瞬时干扰信道和统计干扰信道信息时最优和次优方法的性能。由于最优算法的计算复杂度太高，只比较了载波数较少时最优和次优算法的性能，其中总载波数Ns= 8 ，宏用户所占载波数分别为Np= 2 或Np= 6 。宏用户所允许的最大性能损失率为 0.05，宏基站到宏用户，微基站到微用户，微基站到宏用户的多径数分别为2, 4, 2。从仿真结果可见，本文提出的次优方法与最优算法相比性能损失很小，并且随着宏用户所占载波数的减小而与最优性能差距减少。另外，已知瞬时干扰信道信息时的预编码性能优于已知统计干扰信道信息时的预编码性能。

5 结束语

本文针对异构网中宏用户受到微基站下行传输干扰的场景，考虑多载波宏基站和微基站之间存在频偏的实际情况，提出一种通过设计微基站发射预编码对宏用户进行干扰协调的方法。在已知瞬时干扰信道和统计干扰信道信息的情况下分别提出了最优和次优的预编码设计方法。仿真结果表明，次优算法只需迭代一次就能达到很好的性能，与最优算法的性能差距不大，并且其计算复杂度远远低于最优算法。在未来工作中，我们将进一步考虑宏基站和微基站之间存在由收发机运动造成的随机频偏时的干扰协调方法。

[1]3GPP RP-090536, New SI proposal: LTE heterogeneous network deployments [S]. Qualcomm, Nokia, NSN, 2009.

[2]3GPP, RP-105724, Views on eICIC Schemes for Rel-10 [S].NTT DOCOMO, 2010.

[3]Lee H C, Oh D C, and Lee Y H. Mitigation of inter-femtocell interference with adaptive fractional frequency feuse [C].International Communications Conference, Cape Town, SA,2010: 1-5.

[4]Lee P, Lee T L, and Jenong J. Interference management in LTE femtocell systems using fractional frequency reuse [C].12th International Conference Advanced Communication Technology, Gangwon-Do, Korea, 2010, 2: 1047-1057.

[5]Rangan S. Femto-macro cellular interference control with subband scheduling and interference cancelation [C]. 2010 IEEE GLOBECOM Workshops, Miami, FL, 2010:1663-1666.

[6]Chandrasekhar V, Andrews J G, Muharemovic T,et al..Power control in two-tier femtocell networks [J].IEEE Transactions on Wireless Communications, 2009, 8(8):4316-4328.

[7]Talwar S Y, Himayat S, and Johnsson K. Power control based interference mitigation in multi-tier networks [C]. 2010 IEEE GLOBECOM Workshops, Miami, FL, 2010: 701-705.

[8]3GPP TSG RAN#50, RP-101425, Revised SID proposal:coordinated multi-point operation for LTE [S]. Samsung,2010.

[9]Xu Z K and Yang C Y. Secondary transceiver design in the presence of frequency offset between primary and secondary systems[J].IEEE Transactions onWirelessCommunications,2010, 9(11): 3461-3471.

[10]Li Y G and Stuber G L. Orthogonal frequency division multiplexing for wireless communications[M]. New York,USA: Springer Science-Business Media, 2006, Chapter 3, 4.

[11]Hou X Y, Ling W, Xu Z K,et al.. A precoder for reducing downlink interference from femtocells to macro users based on cognitive radio [C]. 10th International Conference on Signal Processing, Beijing, China, 2010: 1663-1666.

[12]Vandanberghe L and Boyd S. Semidefinite programming [J].SIAM Review, 1996, 38(1): 49-95.

[13]Boyd S and Vandenberghe L. Convex optimization [M].Cambridge: UK, Cambridge University Press, 2004: 257-263.

[14]Knockaert L, Backer B D, and Zutter D D. SVD compression,unitary transforms, and computional complexity[J].IEEE Transactions on Signal Processing, 1999, 47(10): 2724-2729.

[15]Koc C K and Chen G R. Authors’ reply [Computational complexity of matrix inversion][J].IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(4): 1115.