Research on Top-layer Planning and Overall Design Project Decision of Weapon System Based on Analytic Hierarchy Process
WU Rui-wen(武瑞文)
(North Institute for Scientific and Technical Information,NORINCO Group,Beijing 100089,China)
Analytic hierarchy process was developed by Thomas L Saaty in 1971 as a method for decision-making analysis.In this paper,it will be used to study the decision-making for the top-layer planning and overall design projects of modern self-propelled gun-howitzer weapon system.
1 Principle of AHP[1-6]
When solving the problem by using AHP,its various elements involved have to be classified first,their relationships is found out next,and a hierarchy structure can be built then.All the elements can be divided into three categories,including overall goal,criterion and project,i.e.
overall goal…evaluation criteria…alternatives.
Subsequently,the importance(weight)of each criterion to the overall goal is calculated,then the importance(weight)of each alternative to each criterion is analyzed,and finally the importance(weight)of each alternative to the overall goal can be calculated.
Assuming the elements in a layer areA1,A2,…,An,when the calculated weights of these elements to an element in the upper layer are known asw1,w2,…,wn,a matrixA=(aij)can be written as

i.e.aij=wi /wj,andaji=1/aij(i,j=1,2,…,n).That is to say,this equation holds with regard to anyi,j,k,aij×ajk=aik(consistency condition).It shows that the decision makers’judgments are consistent without any contradiction.Letw=(w1,w2,…,wn)T.It can be obtained that
This is a matrix eigenvalue problem,

whereIisnorder matrix.According to linear algebra theory,in order to acquire the non-zero vectorw≠0,nmust be the eigenvalue ofA,and correspondinglywis the eigenvector ofA.Then,it is deduced fromaij×ajk=aikthat the rank ofAis 1,thusAhas only one non-zero eigenvalue.Additionally, the sum ofA's main diagonal elements isn,that is the sum ofA's eigenvalues,thus the only non-zero eigenvalue ofAisn,andA's eigenvalues possess the following relationship,

However,for the actual complex problems,the weight vectorwis unknown;its approximate vectorw'must be calculated.Based on the decision makers’answers,a comparison matrixA'=(aij)can be created to calculate the weight vectorw'thereby.

(λ'maxis the maximum eigenvalue ofA').
But,the reality is so complex that,normally,the decision makers’answers are not consistent.At this moment,A'does not meet the consistencyaij×ajk=aik.It can be proved that the maximum eigenvalueλ'maxof the pairing comparison matrixA'is greater than or equal ton,by using Saaty Theorem,as shown in Eq.(4).
Generally,whenλ'max>n,the necessary and sufficient condition ofλ'max=nis thatA'is a consistent matrix.The consistent index can be introduced as


whereRchanges along with the order of the discriminant matrix.The specific data can be seen from Tab.1.

Tab.1 R for different orders of discriminant matrix
IfI>0.1 or 0.15,it shows that there exists inconsistent data,the consistency must be examined by using the method of rebuilding the pairing comparison matrix,but it is difficult to judge which paired comparison value does not meet the consistency.Ref.[4 -6]provide a method for judging the inconsistent data,that is,calculate the ratios of the given weight valueωi /ωjofωin the eigenvectors,arrange these ratios as a ratio matrix in order,then judge the exceptional value with the greatest differences from all the elements in the original matrix and the ratio matrix,correct the specified value given by experts,reform the discernibility matrix,calculate the eigenvectors and the latent roots again,and examine the consistency,until the consistent indices meet the requirement.
2 Basic Steps of AHP[7-15]
The AHP model block diagram is shown in Fig.1.It can be divided in three steps.
2.1 Establishment of Hierarchy Model
The first step is to build a hierarchy model of the complex problem.The element in the top layer is the overall integrated goal.In all layers below,the decision-makers determine subjectively whether there is re-lationship between the elements and those in the upper layer.Generally,in each layer,except the comprehensive table,it allows up to about seven elements.Numbers of layers are determined according to the constitutive properties of the problem,without any specific boundaries.The bottom layer includes alternatives.
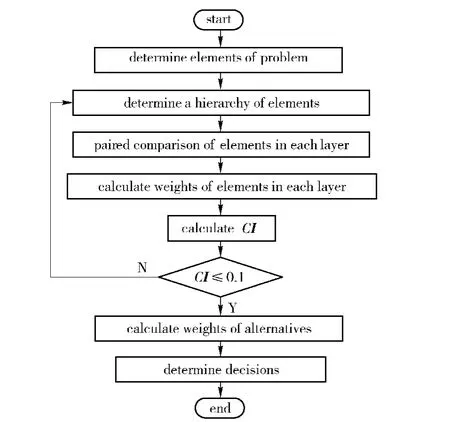
Fig.1 AHP model diagram
2.2 Determination of Weights
The second step is to determine the weights of the elements in each layer.As the basis for evaluation,the elements in a layer related to an element in the upper layer are compared.If there arenelements in comparison,n(n-1)/2 pairs have to be conducted.The resulted values of comparisons are generally taken as 1/9,1/8,…,1/2,1,2,…,8,9 and so on,and their meaning are shown in Tab.2.

Tab.2 Important scale and meaning
Through the above efforts,a pairing comparison matrix in each layer can be obtained,and the weights of the elements in each layer can be calculated then,where the matrix eigenvalue theory in linear algebra is used.When the pairing comparison matrix created based on the decision makers’answers is inconsistent,the matrix should be examined and corrected by using the above methods for inconsistency inspection.
2.3 Weight Calculation of Alternatives
After calculating the weights of the elements in each layer,as the third step of AHP,the weights of alternatives to the overall goal can be calculated ultimately,to obtain the decision project thereby.
3 Overall Design Project Evaluation Decision[16-20]
In accordance with AHP decision-making steps,the decision evaluation on the overall design projects of a self-propelled howitzer system A and another self-propelled gun-howitzer system B is conducted.
3.1 Establishment of Decision Index System
The key of AHP is to establish a whole set of index system for decision analysis.In order to accurately and comprehensively evaluate the overall design projects of two guns,by using Delphi technique,an evaluation index system is determined by several experts in weapon field.In the index system,the goal layer refers to the comprehensive efficiency of weapon system,and the criterion layer includes the first-level indices and the second-level indices,where the first-level indices consist of operability,system accuracy,information capability,logistic support,training capability and economy,and the second-level indices are the sub-indices of the first-level indices,as shown in Fig.2.
3.2 Acquisition and Sorting of Scale Data
While setting up the index system,several experts are invited to conduct the paired comparisons of various elements in a layer related to an element in the upper layer.By considering these experts’ opinions,the scale data table can be obtained,as shown in Tab.3 to Tab.5.
3.3 Calculation of Eigenvaluesand Corresponding Eigenvectors in Each Layer Matrix
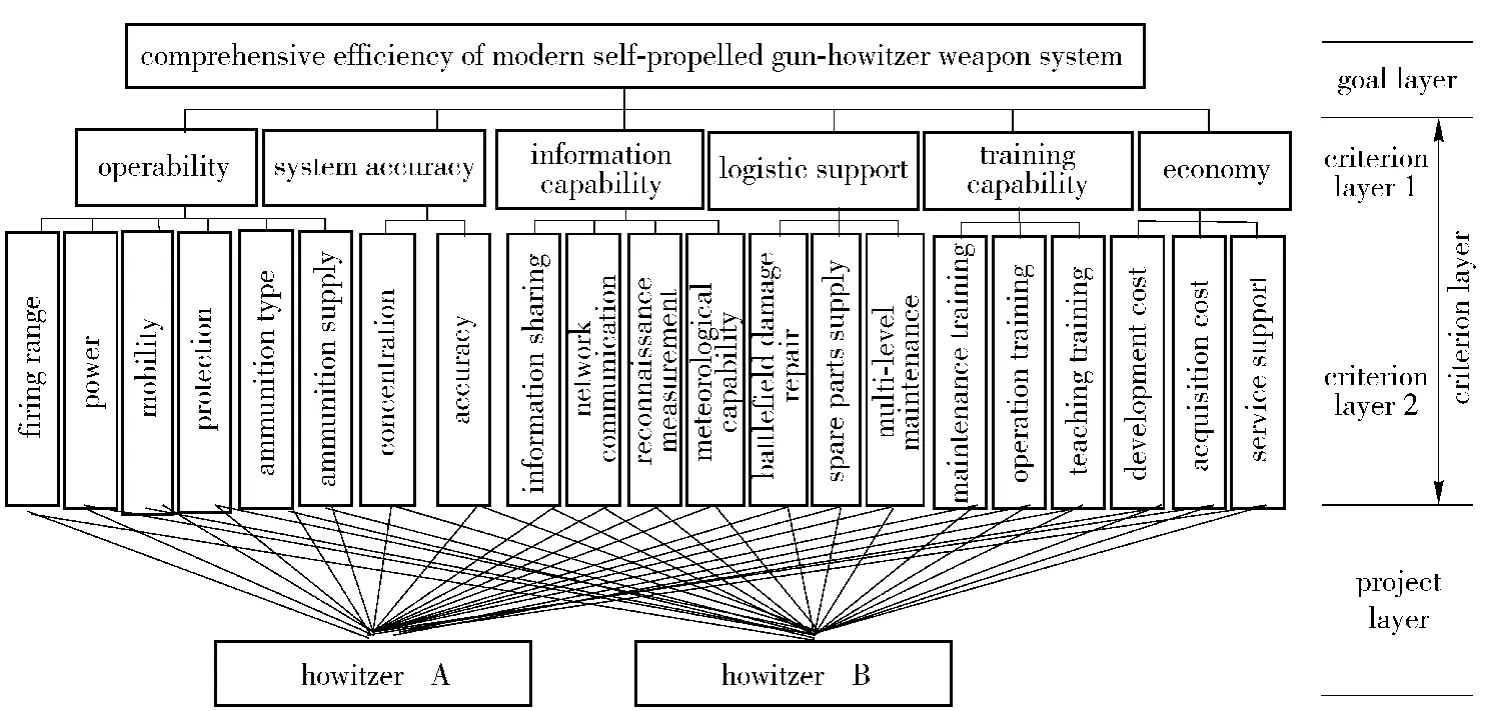
Fig.2 Hierarchy diagram of self-propelled gun-howitzer A and B

Tab.3 Pairing comparison matrix of elements in criterion layer 1

Tab.4 Pairing comparison matrix of elements in criterion layer 2

Tab.5 Pairing comparison matrix of elements in project layer(layer 3)
The eigenvalues and eigenvectors of the above comparison matrix are calculated respectively,where the eigenvalues are used to examine the data consistency,and the corresponding eigenvectors are weight vectors.Generally,the ultimate weight vectors are obtained through the normalization of eigenvectors.The calculated results are shown in Tab.6.
The eigenvectors corresponding to the eigenvalues in Tab.6 should be normalized and reduced to turn into weight vectors.Before normalization,the inconsistent data should be examined and corrected first.
3.4 Examination and Correction of Inconsistent Data
Known from inconsistency examination results in Tab.6,the operability matrix in layer 2 achieves to 0.163 9 more than 0.1,thus,there exists inconsistent data in the operability matrix.According to the processing principle of the inconsistent problems in AHP theory,the following matrix can be obtained by calculatingwi /wj(i,j=1,…,6)in the operability matrix

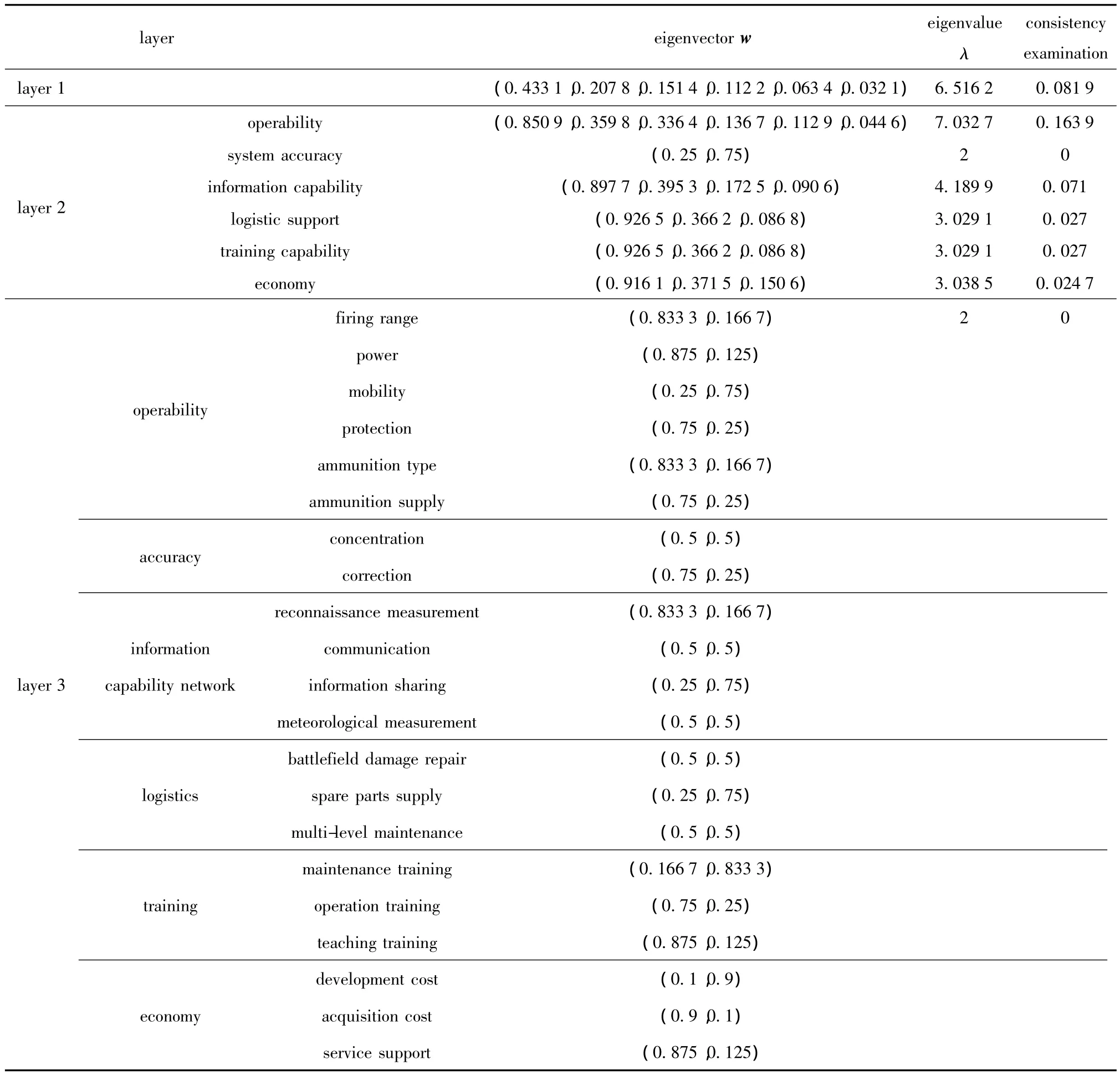
Tab.6 Eigenvalues,eigenvectors and consistency examination results of elements in each layer
Comparing all elements in the originalAandA',the element of the greatest difference is shown asA'underlined element.Correcting the paired comparison value,and according to this principle,the following paired comparison value matrix is ultimately obtained.
3.5 Calculation of Weights of Elements in Each Layer According to Eigenvectors
Firstly,the eigenvectors in Tab.6 are reduced to obtain the normalization results in Tab.7 which refer to weight vectors.Because the results in layer 3 are reduced already,only the normalized results of eigenvectors in layer 1 and 2 are listed in Tab.7.

Tab.7 Weight vectors(all elements in Layer 1 and 2)
Therefore,the weight vectors of layer 2 corresponding to layer 1 can be calculated respectively as follows.
Operability:ω'21=0.433 1ω21=(0.208 1,0.089 5,0.069 3,0.0349,0.0163,0.0150),system accuracy:ω'22=0.207 8ω22=(0.052 0,0.155 9),information capability:ω'23=0.151 4ω23=(0.087 3,0.038 5,0.016 8,0.008 8),logistic support:ω'24=0.112 2ω24=(0.075 4,0.029 8,0.007 1),training capability:ω'25=0.063 4ω25=(0.042 6,0.016 8,0.004 0),economy:ω'26=0.032 1ω26=(0.020 4,0.008 3,0.003 4).
Combining the above results,the weight vectors of the third layer’s elements,from left to right,in Fig.2 are listed below.

3.6 Hierarchy Total Decision
After calculating the weights in each layer,the hierarchy overall weight can be calculated,that is to say,the quantitative selection criterion of the alternatives to the overall goal can be determined.
Denote the weight of the selection criterion of the alternatives asX,thus
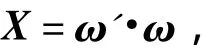
where
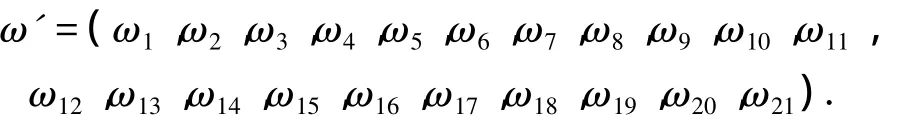
It is a 2×21 matrix composed of the weight vectors of the evaluation results of the 21 factors in the bottom criterion layer to howitzers A and B.The matrix of various componentsωi(i=1,…,21)can be obtained according to the eigenvectors in layer 3 in Tab.6,for example,
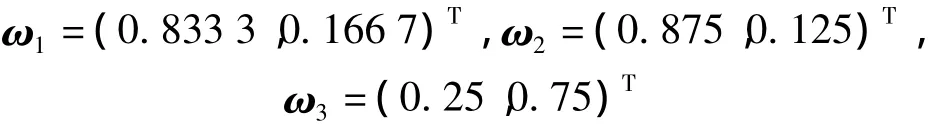
Meanwhile,ωis a 21×1 matrix,so the weight matrixXof the project can be achieved through matrix multiplication.
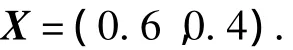
4 Analyses for Calculation Results
1)The obtained evaluation vector matrixXof howitzers A and B shows that the howitzer A’s overall design project is much better than that of howitzer B,and the ratio of the comprehensive efficiency of the former to the latter is 0.6/0.4=1.5.
2)After further calculation,the performances of howitzers A and B for all indices in criterion layer 1 can be compared.Its calculation principle is basically identical to that of the hierarchy total decision.Take the comparison calculation of operability as an example,where the operability ratio of howitzer A to that of B is 0.738 9/0.261 1=2.83.The contrastive results of two howitzers’indices in the layer 1 are shown in Tab.8.


Tab.8 Comparison of calculated results of all indices in criterion layer 1
3)Calculated all indices in criterion layer 1,it can be concluded as follows.
The self-propelled howitzer A is much superior to howitzer B in terms of operability,system accuracy and economy,especially the former costs only one fifth of the latter,and its cost-effectiveness ratio basically meets our country’s current reality.
2)The self-propelled howitzer A is inferior to howitzer B in terms of information capability,logistic support and training capability.From the weight vectors in criterion layer 2,it is known that the howitzer A is not inferior to howitzer B in all indices.Taking the information capability as an example,the howitzer A is much better than B in the reconnaissance measurement,and they are equal to each other in the network communication and meteorological measurement,but there exists larger gap between them in the key information sharing index.It indicates that,under the current condition of information warfare,the experts pay more attention to the battlefield information intercommunication,thus provide a larger weight for it.Meanwhile,it indicates that the howitzer A’s ability should be further enhanced and improved to adapt to the information warfare.The corresponding conclusions can be derived from the analysis of logistic support and training capability as well.
5 Conclusions
AHP is generally used to evaluate and analyze the decision problems,which have uncertainties and multiple evaluation criteria.Based on the overall consideration for the problem,it combines the qualitative analysis with the quantitative analysis,thus quantifies the decision-makers’experience.As one of practical decision methods,it is approaching mature through continuous improvement,and can be widely applied to evaluate multi-criteria and uncertain problems.
The decision-making for overall design projects is the important problem in the weapon systems top-layer planning and overall design.By using AHP,the comprehensive efficiency of weapon systems can be analyzed and evaluated to decide their optimal project.In the evaluation process,a hierarchy model is built to solve the complex and uncertain problems,and a decision-making index system is established.Then,the weights of each layer of the model are determined by experts.Finally,according to the calculated results of the elements in each layer,the weights of the alternatives to the integrated goal are calculated to conduct the hierarchy total decision.An example shows that the overall project of self-propelled gun-howitzer A is much better than that of self-propelled gun-howitzer B digitalized.For example,the comprehensive efficiency of the former is one and a half times of the latter,and its operability,system accuracy and economy are all superior to B.Especially,the cost of former is only one fifth of B.But,for the information capability,the former is inferior to later,and there exist relatively larger gaps between them in the key information sharing index.It reflects that the experts score objectively and they have mastered the current battlefield requirements.Finally,in this paper,the overall projects of two howitzers are evaluated objectively and accurately.
AHP is an effective method for combining the qualitative analysis with the quantitative analysis.In the evaluation of the modern self-propelled gun-howitzer weapon system,the combination of theory with practical experience is required.
[1]LI Gen-shen.Intelligential decision support system for military use[M].Beijing:Ordnance Industry Press,1991.(in Chinese)
[2]LI Huai-zu.Theory for make policy guide[M].Beijing:China Machine Press,1993.(in Chinese)
[3]CHEN Wen-wei.Decision support system and develop[M].Beijing:Tsinghua University Press,1994.(in Chinese)
[4]XIAO Jian-gang.IDSS structural research of object-oriented[J].Make Policy & Decision Support System,1994,(1):40 -46.(in Chinese)
[5]CHEN Shou-yu.Theory and apply of system indistinct decisional[M].Dalian:Dalian Physics and Industry University Press ,1994.(in Chinese)
[6]MA Yun-sheng.DSS& IDSS[M].Beijing:China Textile Industry Press,1995.(in Chinese)
[7]LI Shu-tao.Theory and technology of decision support system[M].Beijing:Beijing Institute of Technology Press,1996.(in Chinese)
[8]GAO Hong-shen.Decision support systems(DSS):theorymethod and example[M].Beijing:Tsinghua University Press,1996.(in Chinese)
[9]XU Nan-rong,ZHONG Wei-jun.Theory and method of scientific decision[M].Nanjing:Southeast University Press,1996.(in Chinese)
[10]LI Tong.System integration of object-oriented method in DSS[J].Make Policy& Decision Support System,1997,(1):24 -29.(in Chinese)
[11]SUN Zhan-shan.DSS and its application[M].Nanjing:Nanjing University Press,1997.(in Chinese)
[12]WEI Shi-xiao,ZHOU Xian-zhong.Multi-attribute decision-theoretic approach and its Application in C3I system[M].Beijing:National Defense Industry Press,1998.(in Chinese)
[13]SUN Bo.Aid DSS research for leadership[J].Academic Journal of Management Science,1998,(3):65 - 73.(in Chinese)
[14]CHEN Wen-wei.Technology of intelligential decision[M].Beijing:Electronic Industry Press,1998.(in Chinese)
[15]HUANG Jing-ping.Design and realize of one type intelligential decision support system[J].Academic Journal of Huazhong Physics and Industry University,1998(9):81-83.(in Chinese)
[16]HOU Yun.Intelligential decision and analysis support system based on knowledge[D].Nanjing:Nanjing University of Science & Technicality,1999.(in Chinese)
[17]PENG Yong-xing.Managerial decision analysis[M].Beijing:Science Press,2000.(in Chinese)
[18]WU Rui-wen.Administrative decision research to informationize project of weapon system[M].Beijing:Ordnance Industry Press,2003.(in Chinese)
[19]WU Rui-wen,WANG Zhao-sheng.A study on the firing accuracy of self-propelled artillery systems[J].Acta Armamentarii,2004,25(7):407 -409.(in Chinese)
[20]WU Rui-wen.Top planning and overall design of modern self-propelled artillery systems[M].Beijing:National Defense Industry Press,2006.(in Chinese)
- Defence Technology的其它文章
- Fault Diagnosis of Bearing Based on Integration of Nonlinear Geometric Invariables
- Influence of Structure Parameters of Double-angle Liner on Jet Formation
- A Novel Kernel for Least Squares Support Vector Machine
- Experimental Investigation on the Ballistic Resistace of Metal Plates Subjected to Impact of Rigid Projectiles
- Research on Matching Relationship Between Number of Initiation Points and Charge Diameter
- Computational and Experimental Investigation on Aerodynamic Characteristics of Terminally Sensitive Projectile with S-C Shaped Fins

