基于复图像OMP分解的宽带雷达微动特征提取方法

罗 迎*① 张 群① 王国正② 管 桦① 柏又青②



基于复图像OMP分解的宽带雷达微动特征提取方法

罗 迎张 群王国正管 桦柏又青

(空军工程大学信息与导航学院 西安 710077)(空军工程大学理学院 西安 710051)

针对宽带雷达中目标微动散射点发生越距离单元走动和方位欠采样条件下的微动特征提取问题，该文提出了一种基于复图像正交匹配追踪 (OMP)分解的微动特征提取新方法。该方法利用目标“距离-慢时间像”的幅度和相位信息，构造复图像空间的微多普勒信号原子集，将向量空间的OMP算法拓展到复图像空间，实现了距离-慢时间平面上目标微动特征的提取。仿真实验表明该方法能够有效提取微动散射点发生越距离单元走动条件下的微动特征，并且可以实现方位欠采样时的微动特征提取。

微动；微多普勒；正交匹配追踪 (OMP)；宽带雷达

1 引言

近年来，雷达目标的“微多普勒(micro-Doppler effect, m-D effect)”效应已成为目标特征提取与识别领域的研究热点，基于微动(Micro-motion)特征的目标识别技术被认为是雷达目标识别技术中最具发展潜力的技术之一。自从2000年V. C. Chen提出微多普勒的概念以来，有关微动特征提取的技术得到了较多的研究，特别是窄带雷达中微动特征提取已经得到了较为广泛的研究。时频分析是使用最为广泛的技术，如V. C. Chen详细分析了高分辨时频分析方法在微动特征提取中的应用；T. Thayaparan等人研究了自适应联合时频分析和小波变换理论用于微多普勒信息的检测和分离，并从直升机和人体回波中成功提取了微多普勒信号；等等。基于微动参数估计的空间目标和地面目标识别技术也得到了较为深入的研究；文献[10,11]还研究了基于微动特征的低分辨雷达多目标分辨技术。

随着宽带雷达信号处理技术的发展与成熟，高分辨成像雷达得到了日趋广泛的应用。在宽带雷达中，若微动点在成像期间没有发生越距离单元走动，则可以通过抽取该微动点所在距离单元信号进行分析来获得其微动特征，如在每个距离单元回波中采用chirplet变换、EMD分解、AM-LFM分解等方法分离微多普勒信号片段，由分离出的信号片段来重构目标的微动特征。然而，由于宽带雷达的距离高分辨能力，目标的微动通常导致散射点发生越距离单元走动，散射点回波能量分布在多个距离单元中，每个距离单元回波无法包含微动点的全部回波信号，上述方法运算复杂且难以取得较好效果。更进一步地，当目标微动速度较大时，微多普勒谱宽较大，而雷达脉冲重复频率往往不可能很高，这将导致微多普勒信号的欠采样，如雷达发射信号载频为10 GHz、微动点旋转频率为4 Hz、旋转半径为6 m时，微多普勒谱宽将达到20 kHz，若要保证对微多普勒谱的奈奎斯特采样，将对雷达脉冲重复频率提出很高的要求。当雷达脉冲重复频率小于两倍微多普勒谱宽时，微多普勒信号将在频域出现卷绕。这也给现有微动特征提取方法带来了很大困难。

针对宽带雷达中目标微动散射点发生越距离单元走动和方位欠采样条件下的微动特征提取问题，本文提出了一种基于复图像正交匹配追踪(Orthogonal Matching Pursuit, OMP)分解的宽带雷达微动特征提取方法。由于宽带雷达的距离高分辨能力，我们可通过分析目标1维距离像序列的变化特征来挖掘目标的微动特征，即从目标回波“距离-慢时间像”入手来获取目标微动特征。本文以典型的旋转形式微动为例，通过利用“距离-慢时间像”的幅度和相位信息，构造复图像空间的微多普勒信号原子集，将向量空间的OMP算法拓展到复图像空间，实现了距离-慢时间平面上旋转目标微动特征的提取。该方法能够有效提取微动散射点发生越距离单元走动条件下的微动特征，并且可以实现欠采样条件下的微动特征提取。仿真实验表明该算法具有较好的鲁棒性。

2 旋转微动目标的宽带雷达回波

线性调频(LFM)信号是宽带雷达中应用最为广泛的波形，因此我们以线性调频信号为例来推导旋转微动目标的宽带雷达回波表达式。建立如图1所示的雷达与目标几何模型，图中为全局坐标系，为本地坐标系，3个坐标轴分别与的对应坐标轴平行，点在坐标系中的初始坐标为。雷达位于原点。假设目标由以速度平动到，同时，目标上一个散射点绕点以角速度旋转，点在本地坐标系中的坐标为。令。

图1 雷达与旋转微动目标的几何模型

(2)

根据图1中的几何关系，可以得到

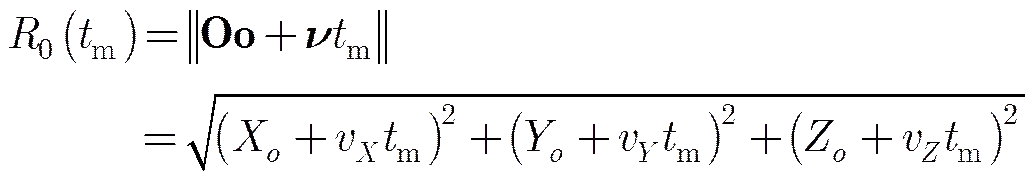
上式用泰勒级数展开，忽略高次项后得到

(5)

(7)

将上式代入式(3)，可得

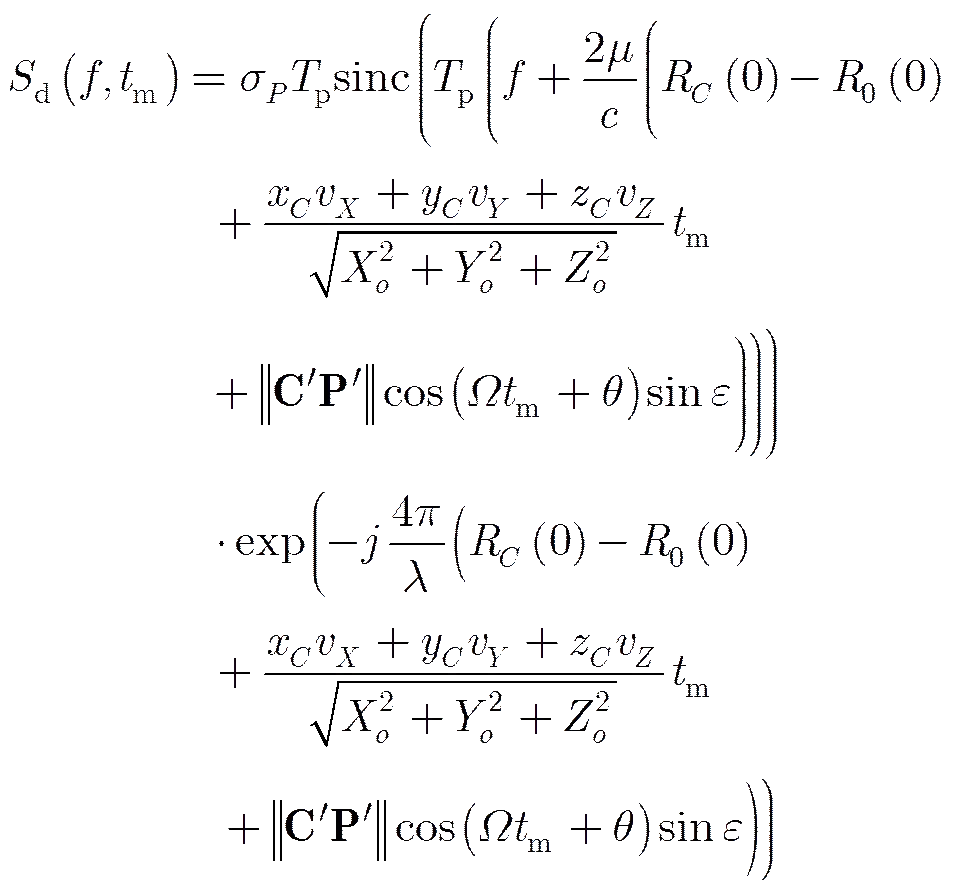
(10)

分析式(10)可知，目标回波距离-慢时间像的相位即包括了由目标微动引起的余弦项，还包括了由目标主体相对雷达运动引起的关于的1次项。对于某个给定的，对式(10)的相位关于求导并除以，即得到信号的瞬时频率

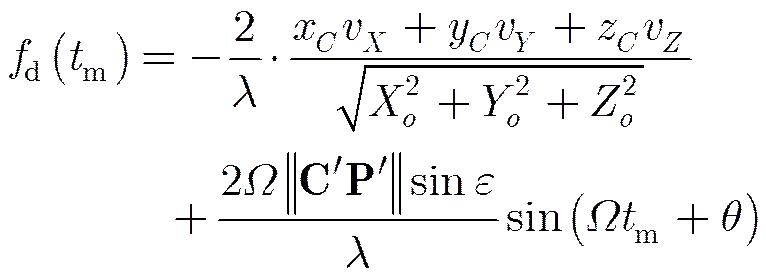
上式右边第1项为目标主体的多普勒频率，第2项则为微动点的微多普勒频率。令

,,

则式(11)可以重写为

式(13)即为线性调频信号宽带雷达中旋转微动的回波表达式。可以看出，式(13)的模值将在距离-慢时间平面上呈现为基线为、频率为、振幅为、初相为的余弦曲线，这表明微动点在多个距离单元之间发生了走动；相位则由参数确定。

3 复图像OMP分解算法

在信号处理中，信号的分解与重构具有十分重要的意义。近年来，随着信号处理理论的发展，信号的非正交分解得到了广泛的重视。Mallat和Zhang首先与1993年提出了“匹配追踪(Matching Pursuit, MP)”的思想，通过将信号分解到一组过完备的非正交基上，从而得到信号的一个稀疏表达，实现对信号特征的高效提取。在MP算法基础上，Y. C. Pati等人进一步提出了“正交匹配追踪(Orthogonal Matching Pursuit, OMP)”的思想，通过将字典中的原子按施密特正交化方法进行正交化处理，然后再用类似MP算法的方法实现信号的迭代分解，这使得该算法能够以比MP更快的速度收敛。由于分解效率高且又简单易行，OMP算法近年来在信号处理特别是稀疏信号处理中得到了广泛应用。因此，本文拟采用OMP算法来提取目标微动特征。

由OMP算法原理可知，字典中的原子应按照待分解信号的内在特性来构造。根据微动目标的回波表达式(13)，在对回波进行离散化后，假设在快时间频域上有个采样点，在慢时间域共发射了个脉冲，则离散化后的距离-慢时间回波信号为的矩阵：

(15)

显然，不同于通常的向量信号分解，式(15)定义的原子集中的原子均为复图像，因此需要将空间的OMP算法拓展到空间。定义空间中的内积运算如下：

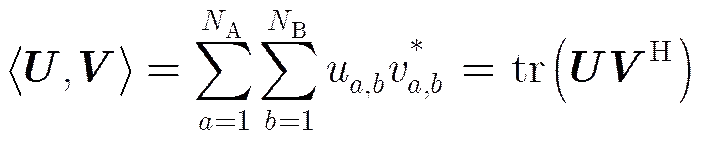
(17)

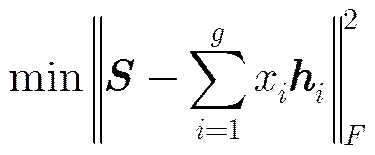
根据最小二乘法，可得(证明见附录A)：

(20)

从原子集中原子的构造方法可以看出，每个原子由幅度与相位两部分构成，在PRF低于微多普勒信号奈奎斯特采样频率时，尽管微多普勒信号和原子的相位均会产生卷绕，但幅度信息并不受欠采样的影响，因此该算法在理论上适用于欠采样条件下的微多普勒信号分析与特征提取。但由于距离分辨率的限制，当距离-慢时间平面上的余弦曲线振幅小于距离分辨单元时，原子幅度中的2维sinc函数基本不随的变化而变化，从而失去了在欠采样条件下准确提取微多普勒信号特征的能力。不过，当小于距离分辨单元时，微多普勒信号谱宽较小，如雷达发射信号载频为10 GHz、带宽500 MHz、微动点旋转频率为4 Hz、为0.1 m时，微多普勒谱宽大约为335 Hz，一般雷达的PRF都可以满足过采样要求。

由于在构造原子集时采用了5个变量，这将导致原子集里的原子数量很大。当目标主体为平稳运 动时，目标主体相对雷达转动引起的多普勒频移可以被估计，因此变量中的取值基本可以确定，从而将5个变量减为4个变量，达到降低运算量的目的。

4 仿真验证与性能分析

4.1算法有效性验证

仿真参数设置如下：雷达位于坐标原点，发射信号载频为10 GHz，脉宽，带宽为500 MHz，距离分辨率为0.3 m。脉冲重复频率PRF=1000 Hz。目标参考点的初始坐标为(30 km, 0 km, 0 km)，目标运动速度向量为，目标由3个旋转散射点构成，当以参考点坐标作为目标本地坐标系的原点时，旋转中心在本地坐标系中的坐标为(5 m, 5 m, 5 m)，旋转角速度向量为，角速度大小，旋转半径为2.8284 m。计算可得微多普勒谱的带宽大约为2369.6 Hz，可见脉冲重复频率低于奈奎斯特采样率。图3(a)给出了目标回波的距离-慢时间像，由于微动散射点的越距离单元走动，图中可以清晰看到3条余弦曲线。

采用本节所提算法提取目标回波距离-慢时间像上的微多普勒信号，设最大迭代次数，得到结果如表1所示。从表中数据可以看出，随着迭代次数的增加，分解得到的信号能量逐渐降低。该算法成功提取出了3个散射点对应的微动特征，的取值为5.0 m,的取值位于2.7 m和3.0 m之间，的取值为1.0 Hz，均与理论值接近。除了第7组参数外，的取值均为0.05 Hz，也与理论值接近。将表1中的信号分解结果重新组合成一个新的距离-慢时间像如图3(b)所示，可见与图3(a)所示的原始距离-慢时间像十分吻合。这验证了所提算法的有效性。

图3 算法有效性验证

表1目标回波的复图像OMP分解结果

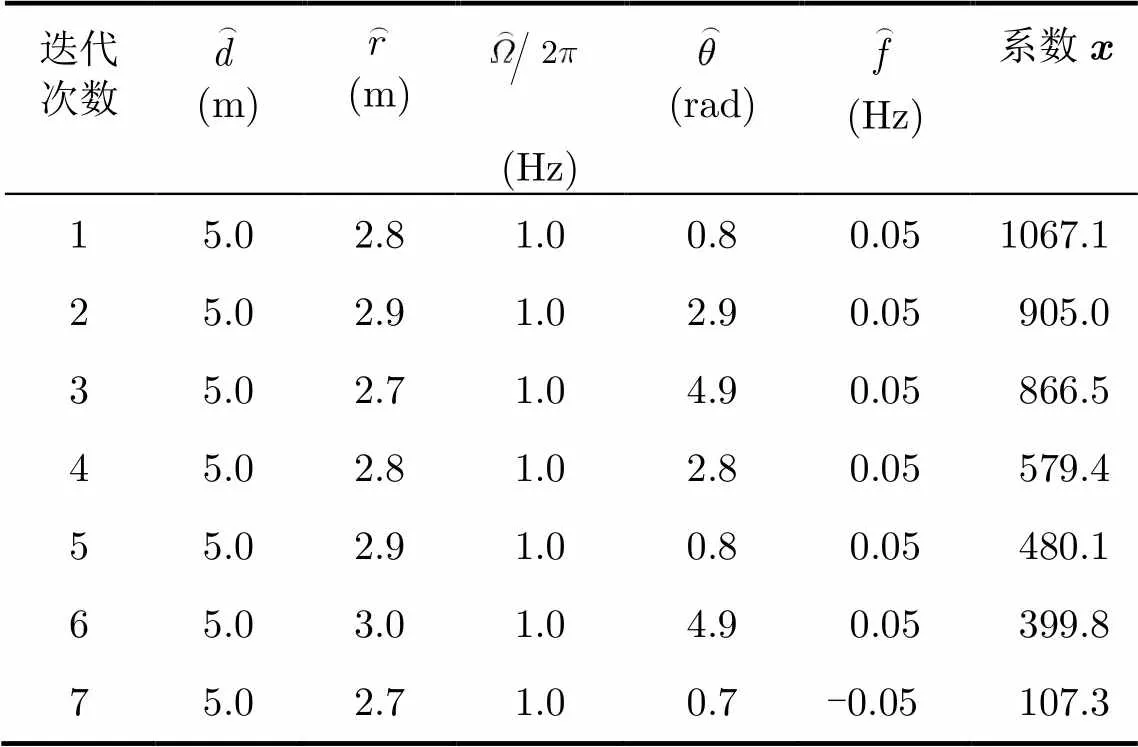
迭代次数(m)(m)(Hz)(rad)(Hz)系数x 15.02.81.00.80.051067.1 25.02.91.02.90.05 905.0 35.02.71.04.90.05 866.5 45.02.81.02.80.05 579.4 55.02.91.00.80.05 480.1 65.03.01.04.90.05 399.8 75.02.71.00.7-0.05 107.3

4.2鲁棒性分析

表2 时目标回波的复图像OMP分解结果

表2 时目标回波的复图像OMP分解结果

迭代次数(m)(m)(Hz)(rad) (Hz)系数x 102.61.02.90625.3 202.91.02.90542.7 302.91.00.80504.1 402.91.00.70467.6 502.81.15.20433.2 602.81.05.30366.2 702.81.02.90312.3

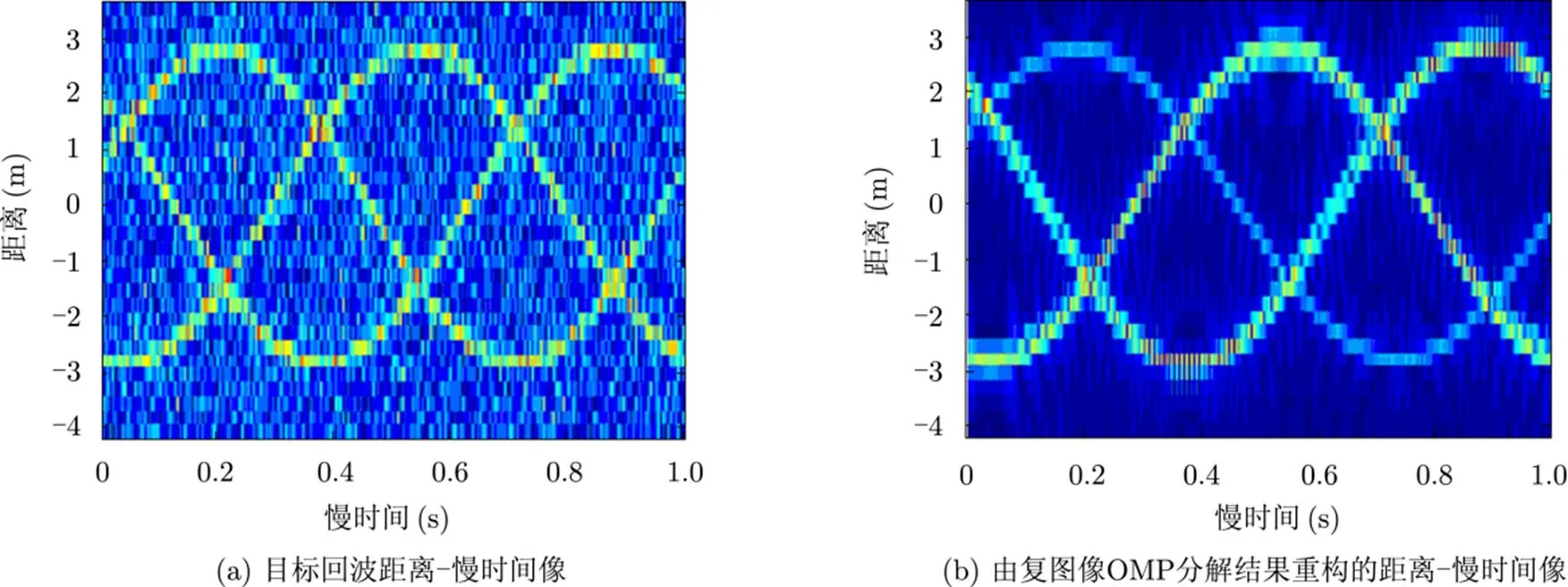
图4 鲁棒性分析()

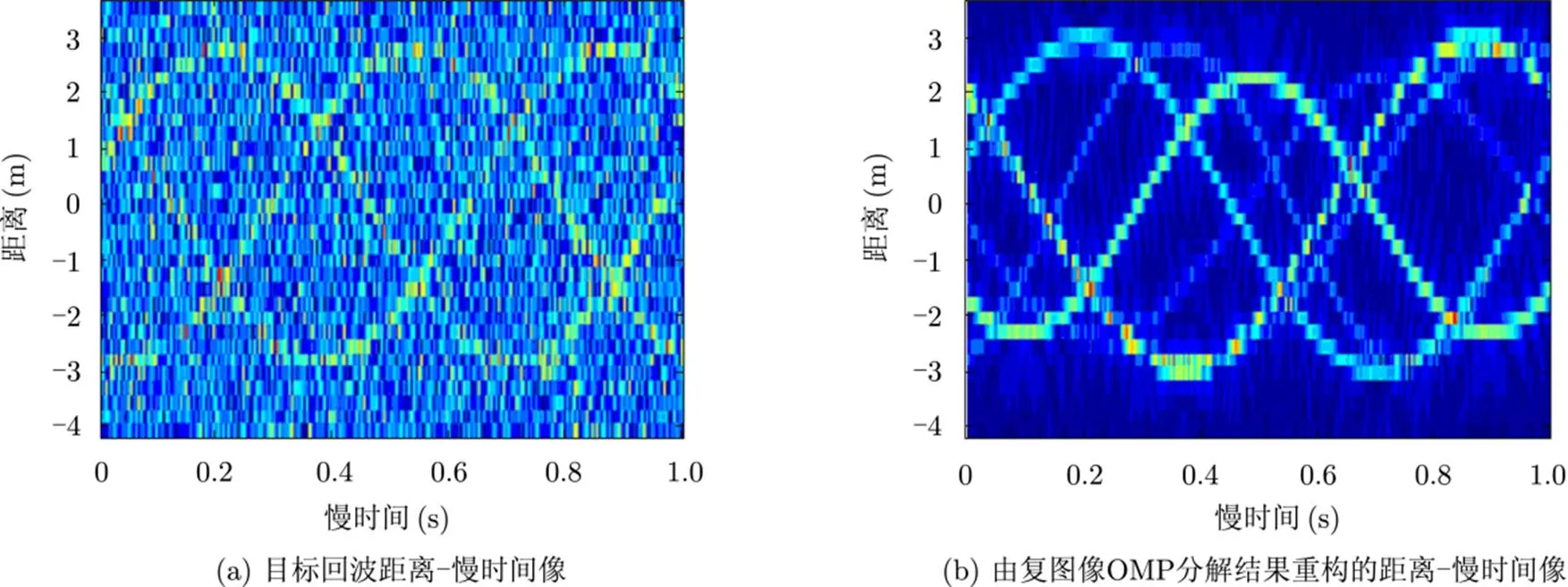
图5 鲁棒性分析()

表3 时目标回波的复图像OMP分解结果

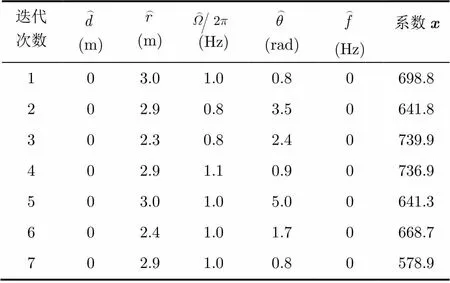
表3 时目标回波的复图像OMP分解结果

迭代次数(m)(m)(Hz)(rad)(Hz)系数x 103.01.00.80698.8 202.90.83.50641.8 302.30.82.40739.9 402.91.10.90736.9 503.01.05.00641.3 602.41.01.70668.7 702.91.00.80578.9

以上仿真表明，该算法具有较为良好的抗噪性能。

5 结束语

本文提出了一种基于复图像OMP分解的宽带雷达微动特征提取新方法。在推导微动目标宽带信号回波表达式的基础上，利用目标回波距离-慢时间像的幅度和相位信息，将向量空间的OMP算法拓展到复图像空间，实现了距离-慢时间平面上旋转目标微动特征的提取。该方法不仅能够提取微动散射点发生越距离单元走动条件下的微动特征，并且可以实现欠采样条件下的微动特征提取。仿真实验表明该方法具有良好的鲁棒性。尽管本文是以线性调频信号为例来推导算法的实施过程，但对于其他形式的宽带雷达信号如非线性调频信号、相位编码信号等，也可以采取类似的思想建立原子集以实现信号的分解。需要说明的是，由于在构造原子集时涉及的变量较多，因此原子集中原子数量通常很大，这使得算法的计算量较大。但随着硬件计算速度的不断增加和并行运算技术的发展，有望在将来实现算法的实时处理。

附录A

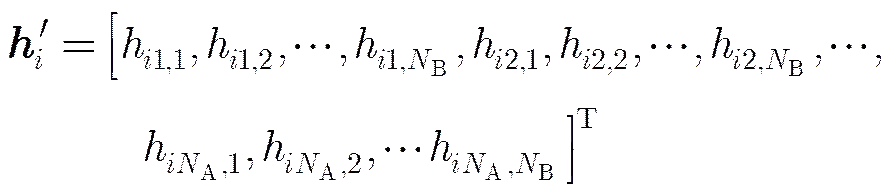
根据最小二乘法，可得

其中

因此有

附录B

上式等价于

,

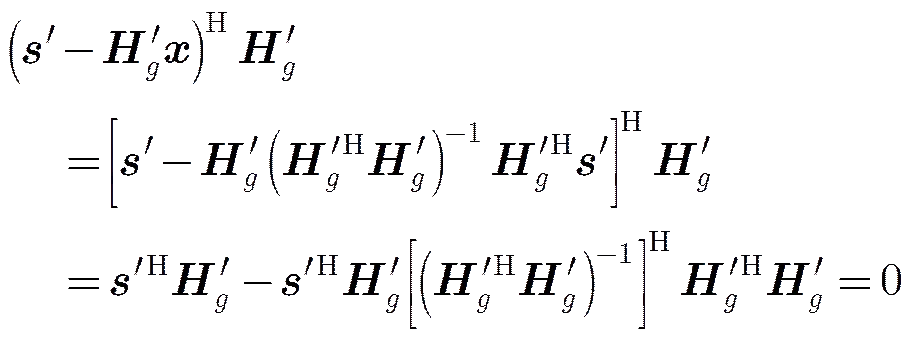
[1] 张群, 罗迎, 何劲. 雷达目标微多普勒效应研究概述[J]. 空军工程大学学报(自然科学版), 2011, 12(2): 22–26.

Zhang Qun, Luo Ying, and He Jin. Review of researches on micro-Doppler effect of radar targets[J].(), 2011, 12(2): 22–26.

[2] Chen V C. Analysis of radar micro-Doppler signature with time-frequency transform[C]. Proceedings of the 10th IEEE Workshop on Statistical Signal and Array Processing, Pocono Manor, PA, USA, 2000: 463–466.

[3] Chen V C, Li F, Ho S S,.. Micro-Doppler effect in radar: phenomenon, model and simulation study[J]., 2006, 42(1): 2–21.

[4] Chen V C and Li F. Analysis of micro-Doppler signatures[J].&, 2003, 150(4): 271–276.

[5] Thayaparan T, Abrol S, Riseborough E,.. Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J].&, 2007, 1(4): 289–299.

[6] 关永胜, 左群声, 刘宏伟, 等. 空间进动目标微动参数估计方法[J]. 电子与信息学报, 2011, 33(10): 2427–2432.

Guan Yong-sheng, Zuo Qun-sheng, Liu Hong-wei,.. Micro-motion parameters estimation of space precession targets[J].&, 2011, 33(10): 2427–2432.

[7] Gao Hongwei, Xie Lianggui, Wen Shuliang,.. Micro- Doppler signature extraction from ballistic target with micro- motions[J]., 2010, 46(4): 1969–1982.

[8] Ghaleb A, Vignaud L, and Nicolas J M. Micro-Doppler analysis of wheels and pedestrians in ISAR imaging[J]., 2008, 2(3): 301–311.

[9] 黄健, 李欣, 黄晓涛, 等. 基于微多普勒特征的坦克目标参数估计与身份识别[J]. 电子与信息学报, 2010, 32(5): 1050–1055.

Huang Jian, Li Xin, Huang Xiao-tao,.. Micro-Doppler features based parameter estimation and identification of tank[J].&, 2010, 32(5): 1050–1055.

[10] 关永胜, 左群声, 刘宏伟. 高噪声环境下微动多目标分辨[J]. 电子与信息学报, 2010, 32(11): 2630-2635.

Guan Yong-sheng, Zuo Qun-sheng, and Liu Hong-wei. Micro- motion targets resolution in a high noise environment[J].&, 2010, 32(11): 2630–2635.

[11] 黄小红, 贺夏, 辛玉林, 等. 基于时频特征的低分辨雷达微动多目标分辨方法[J]. 电子与信息学报, 2010, 32(10): 2342– 2347.

Huang Xiao-hong, He Xia, Xin Yu-lin,.. Resolving multiple targets with micro-motions based on time-frequency feature with low-resolution radar[J].&, 2010, 32(10): 2342–2347.

[12] 金光虎, 高勋章, 黎湘, 等. 基于chirplet的弹道目标逆合成孔径雷达回波分解[J]. 电子与信息学报, 2010, 32(10): 2353–2358.

Jin Guang-hu, Gao Xun-zhang, Li Xiang,.. Inverse synthetic aperture radar echo decomposition of ballistic target based on chirplet[J].&, 2010, 32(10): 2353–2358.

[13] Bai Xueru, Xing Mengdao, Zhou Feng,.. Imaging of micromotion targets with rotating parts based on empirical- mode decomposition[J]., 2008, 46(11): 3514–3523.

[14] 贺思三, 周剑雄, 赵会宁, 等. 基于AM-LFM分解的微动信号提取[J]. 电子与信息学报, 2010, 32(3): 554–558.

He Si-san, Zhou Jian-xiong, Zhao Hui-ning,.. Micro- Doppler signal extraction based on AM-LFM decomposition[J].&, 2010, 32(3): 554–558.

[15] Zhang Q, Yeo T S, Tan H S,.. Imaging of a moving target with rotating parts based on the Hough Transform[J]., 2008, 46(1): 291–299.

[16] Mallat S G and Zhang Z. Matching pursuits with time- frequency dictionaries[J]., 1993, 41(12): 3397–3415.

[17] Pati Y C, Rezaiifar R, and Krishnaprasad P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]. Proceedings of 27th Annual Asilomar Conference of Signals, Systems, and Computers, Pacific Grove, CA, Nov. 1993, Vol. 1: 40–44.

[18] Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]., 2007, 53(12): 4655– 4666.

[19] 李玺, 顾红, 刘国岁. ISAR成像中转角估计的新方法[J]. 电子学报, 2000, 28(6): 44–47.

Li Xi, Gu Hong, and Liu Guo-sui. A method for estimating the rotation angle of the ISAR image[J]., 2000, 28(6): 44–47.

Micro-motion Signature Extraction Method for Wideband Radar Based on Complex Image OMP Decomposition

Luo YingZhang QunWang Guo-zhengGuan HuaBai You-qing

(Institute of Information and Navigation, Air Force Engineering University,Xi’an 710077, China)(Institute of Science, Air Force Engineering University,Xi’an 710051, China)

In order to extract the micro-motion signatures in condition of Migration Through Range Cells (MTRC) of micro-motional scatterers and azimuthal undersampling in wideband radar, a method based on the Orthogonal Matching Pursuit (OMP) decomposition of the complex image is proposed. By making use of the amplitude and phase information of “range-slow-time image”, a set of micro-Doppler signal atoms is constructed in the complex image space. The OMP algorithm in vector space is then extend to the complex image space to obtain the micro-motion parameters. Simulations demonstrate the proposed method can extract the micro-motion signatures when MTRC of micro-motional scatterers is occurred, and can also work well when the sampling rate is lower than the Nyquist sampling rate.

Micro-motion; Micro-Doppler; Orthogonal Matching Pursuit (OMP); Wideband radar

TN957

A

2095-283X(2012)04-0361-09

10.3724/SP.J.1300.2012.20065

罗 迎(1984-)，男，助教/博士研究生，在《IEEE Transactions on Geoscience and Remote Sensing》、《IEEE Trans- actions on Aerospace and Electronic Systems》、《Sci China Inf Sci》、《电子学报》等国内外学术期刊和会议录上发表和录用论文50余篇。主要研究方向为雷达成像与目标识别。E-mail: luoying2002521@163.com

张 群(1964-)，男，教授，博士生导师，IEEE Senior Member，中国电子学会无线电定位技术分会委员。发表学术论文150余篇，其中SCI、EI检索70余篇次。主要研究方向为雷达成像、目标识别、信息对抗等。E-mail: zhangqunnus@gmail.com

王国正(1960-)，男，教授，研究方向为应用数学及其在雷达信号处理中的应用。 E-mail: wgz1210@163.com

管 桦(1962-)，男，副教授，研究方向为雷达成像与目标识别。 E-mail: guanxh@sina.com

柏又青(1959-)，女，副教授，研究方向为应用数学及其在雷达信号处理中的应用。 E-mail: yqbai_59@hotmail.com

2012-09-12收到，2012-11-12改回；2012-11-22网络优先出版

国家自然科学基金(61201369, 61172169)资助课题

罗迎 luoying2002521@163.com