永磁交流伺服自抗扰直接转矩控制
黄祯祥,吴 峻,邓怀雄
(湘潭大学,湖南湘潭411100)
0引 言
与异步电动机相比,永磁同步电动机(以下简称PMSM)不需要无功励磁电流,具有效率高、功率因数高、力矩惯量比大、定子电流和定子电阻损耗小等特点,且转子参数可测、控制性能好,在中小容量交流伺服系统中得到了非常广泛的应用[1-2]。PMSM目前的控制方法主要采用矢量控制和直接转矩控制(以下简称DTC)两种。基于定子电流的矢量控制技术比较成熟,是常用的控制方法。而基于定子磁场的DTC控制从20世纪90年代中期开始应用于异步电机[3],后来通过Zhong L等人的努力,DTC控制成功应用于永磁同步电动机[4-5]。相比矢量控制方法,基于定子磁场的DTC控制可以直接对电机的磁链和转矩进行控制,省略了复杂的坐标变换等单元,并具有对电机参数的依赖性小、控制系统简单、转矩响应快等优点。但由于转子转速和定子电流的强耦合使系统具有很强的非线性,特别在系统存在不确定性时,这种非线性使系统难以达到高精度伺服控制的要求。
目前解决PMSM精确伺服控制问题,通常采用非线性控制方法,主要有变结构控制、微分几何和无源性理论等。特别是文献[6]提出的非线性控制器——自抗扰控制器(以下简称ADRC)能实时观测补偿系统的内扰和外扰,给设计带来了方便。同时ADRC设计不依赖系统的数学模型,有着较好的鲁棒性。本文将ADRC应用于PMSM调速系统的DTC控制方案中,用以解决传统PI控制所无法克服的快速性能与稳态性能之间的矛盾,抑制PMSM在运行过程中由于电机的定子电阻、粘滞摩擦系数和负载转矩的变化以及其他不可预测的外界扰动对系统转速所造成的影响,使得系统对系统参数变化和外部扰动具有较强的鲁棒性。仿真结果表明,本系统具有抗扰动能力强、动态控制性能优越、控制精度高和动态响应快等特点,对不同参考转速给定具有更好的适应性。
1 PMSM的直接转矩控制机理
对于隐极式PMSM,其电磁转矩与定子磁链的表达式分别:
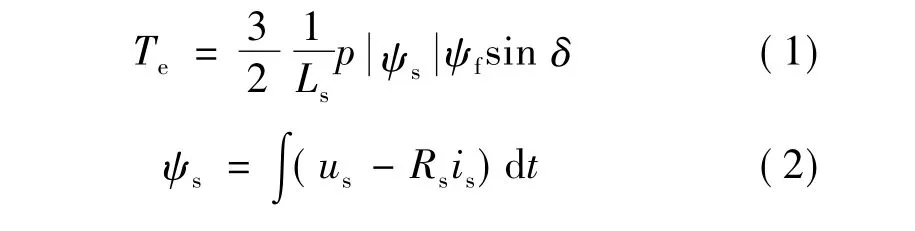
电磁转矩平衡方程:
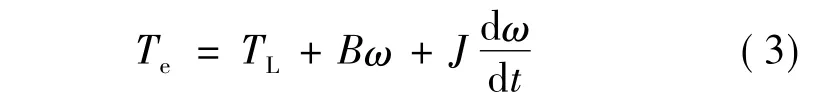
由式(1)可知,如果磁链一定,则电磁转矩Te是功角δ(定子磁链和转子磁链的夹角)的函数。由式(2)可知,选择合适的空间电压矢量可改变定子磁链旋转速度和方向,从而可以瞬时调整功角δ,实现转矩的动态直接控制。而式(3)表明电机的转速ω与电磁转矩Te成积分关系,改变Te,就可通过积分环节实现转速调节。
PMSM的DTC控制模型中,式(1)~式(3)表面上只使用了定子电阻Rs一个电机参数,准确观测定子电阻可达到理想的控制性能。但实际上定子电阻因电机的发热而变化,是时间的函数,很难实时观测。而只要观测的定子电阻出现误差,就会使估计的磁链和转矩出现误差,从而影响调速效果;同时由于系统存在负载机械摩擦和转矩扰动等干扰,转子转速和定子电流又存在强耦合,系统转动惯量也具有时变性等,使得伺服系统在低速运行时转速精度显著下降。为了提高精度,传统PI速度控制器为提高静态开环增益不得不采用较大的积分环节,从而加剧了系统快速性和稳态精度之间的矛盾。同一个PI参数也无法适用于不同的电机转速,因此对控制精度要求较高的场合,PI控制难以取得令人满意的调速性能。
2自抗扰控制器设计
自抗扰控制技术是一种实用的控制系统非线性综合方法。自抗扰控制器主要由跟踪微分器(TD)、扩展状态观测器(ESO)和非线性状态误差反馈控制律(NSEFL)三部分组成。自抗扰控制器的设计能处理确定系统和不确定系统的控制问题,在无需知道外扰模型的条件下能很好地对外扰进行抑制,实现控制不用区分系统是否线性,不用辨识,解耦控制只需考虑静态耦合,容易控制时滞系统,所以它对时变、非线性、强耦合、大时滞等被控对象,均能给出很好的控制效果[7-8]。
设被控对象的状态方程如下:
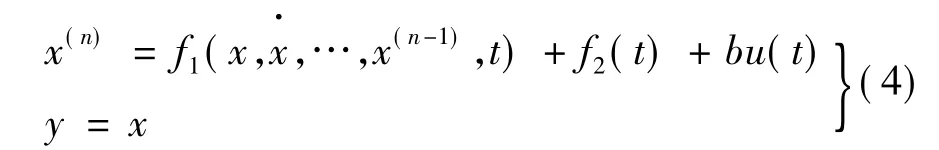
式中:b为系统控制量增益;u(t)为系统控制量;f1(x,,…,x(n-1),t)为系统非线性函数;f2(t)为系统未知外扰;x为可观测状态量;y为被控对象输出。

PMSM电磁转矩平衡方程改写如下:
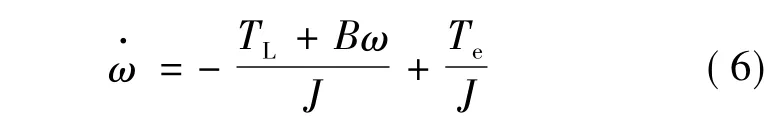

由式(7)可以看出,未知扰动与负载转矩TL的扰动所造成的转速波动可以在综合扰动项w(t)中反映出来,为抑制综合扰动可通过对w(t)进行观测并补偿来实现。扩展状态观测器能解决模型未知部分和外部未知扰动综合对控制对象的影响,为此设计一个扩展的状态量来跟踪模型未知部分和外部未知扰动的影响,然后给出控制量进行补偿,将控制对象变为普通的积分串联型控制对象,实现动态系统反馈线性化。下面设计自抗扰控制器来解决这一问题,从而实现PMSM的速度控制。
被控对象PMSM的ADRC方程描述如下:
微分–跟踪器(TD):

扩张状态观测器(ESO):
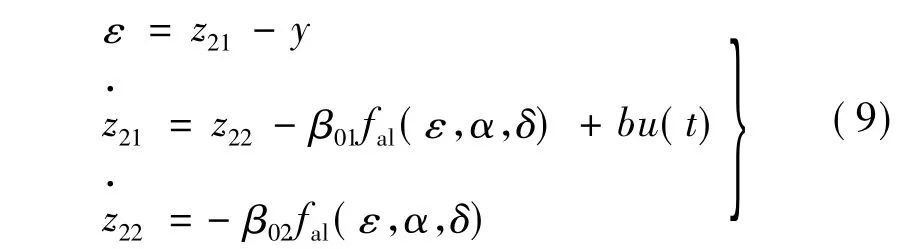
非线性反馈控制律(NLSEF):
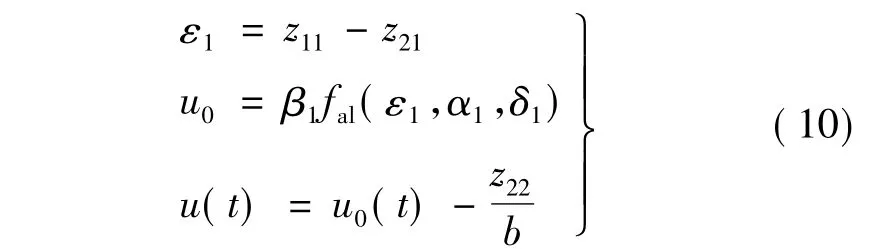
最优控制函数 fal的表达式[4]:
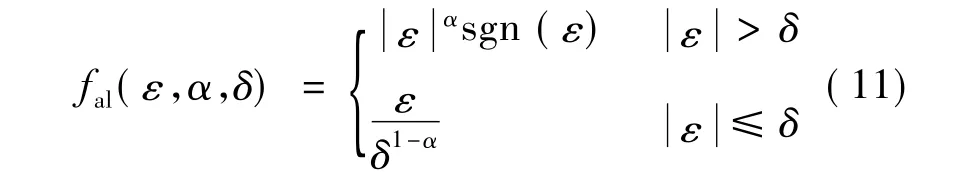
式中:v为ADRC的给定信号;z11为v的跟踪信号;r为跟踪速度因子;y为系统输出;z21为y的跟踪信号;z22为w(t)的跟踪信号;ε为误差信号;α为非线性因子;δ为 ESO滤波因子;β01、β02为输出误差校正增益;β1为误差增益。
具体的控制器结构如图1所示。
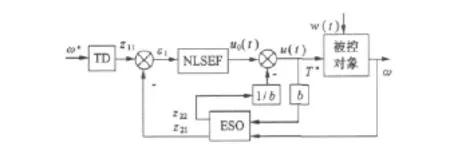
图1 ADRC控制器结构图
图1中ω*、T*分别是速度给定与转矩给定,ω是系统速度反馈信号,z11是ω*的跟踪信号,z21是ω的跟踪信号,z22是扰动w(t)的跟踪信号。在图1中,TD为ω*安排了过渡过程,得到了较为平滑的输入信号,使得系统响应迅速且没有超调。文献[9]的研究表明,安排合适的参考轨迹过渡过程是解决传统PID控制的响应快速性和超调性之间的矛盾的有效办法,同时使系统的鲁棒性、稳定性和适应性也得到了大大的提高;结构中ESO环节对各个状态变量进行实时估计,同时也对内外扰动(包括负载扰动、转动惯量和定子电阻的变化以及其它未知扰动)和系统不确定性模型进行精确观测,实现动态系统的反馈线性化,使被控对象的不确定性在反馈中加以补偿,达到重构对象的目的;NLSEF实现对综合扰动的补偿和“小误差大增益,大误差小增益”的非线性控制[10],以提高稳态控制精度。
3仿真实验与分析
为了验证所设计控制器的有效性,我们根据图2的DTC控制原理图在Matlab/Simulink中构造了基于ADRC的DTC控制系统仿真模型,同时也搭建了基于传统PI控制器的DTC控制系统模型。
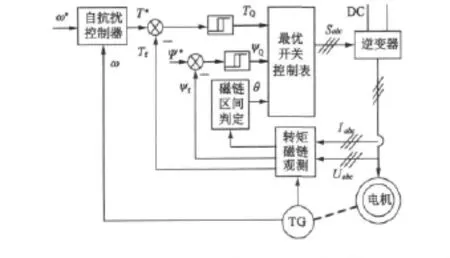
图2 基于ADRC的DTC控制系统
PMSM 相关参数:Rs=1.9 Ω,Lq=Ld=0.01 H,ψf=0.353 Wb,J=7.24 ×10-4kg·m2,B=1.4 ×10-7N·m/(r·min-1),p=2,ωref=1 000 r/min。仿真时ADRC 控制器的参数选定:b=1 381.2,β01= β02=4 000,β1=3,α =0.8,δ=0.05,α1=0.8,δ1=0.04;PI控制器的参数:KP=3,KI=0.45。图3是系统在不同给定下的转速响应曲线。结果表明,ADRC相比PI控制具有更快的响应速度和更高的稳态精度,超调大幅度减小;且在不同的转速给定下ADRC控制器具有更强的适应性,特别在低速运行时体现出了良好的动态性能。

图3 不同给定时的系统响应对比
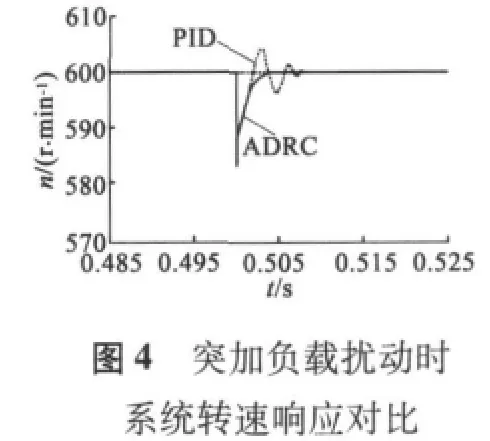
为研究系统对突变负载扰动的抵抗能力,仿真中系统在0.5 s时突然加入一个50%额定转矩的负载扰动,图4是ADRC控制与PI控制时对突变负载扰动时转速的响应曲线,从图4中可以看出,当负载扰动突变时,ADRC比PI具有更小的转速变化与更快的恢复时间。图5为系统转动惯量变为原来的2倍时的速度响应曲线。传统的DTC控制由于PI参数未加以调节从而引起了剧烈的振荡。以上仿真实验说明ADRC不仅对负载扰动或外界干扰,而且对系统未知参数均具有良好的鲁棒性。

4结 语
根据永磁交流伺服直接转矩控制的模型特点,将ADRC控制器应用于永磁交流伺服系统DTC的调速控制中,较好地抑制了PMSM在运行过程中因系统参数变化与外部扰动所带来的影响,使得系统具有良好的动态、静态性能与较强的鲁棒性。且在相同的扰动下,相比经典PI控制器在不同的转速给定下具有更强的适应性和更好的动态控制性能。
[1] 秦忆.现代交流伺服系统[M].武汉:华中理工大学出版社,1995.
[2] 王宏,于泳,徐殿国.永磁同步电动机位置伺服控制系统[J].中国电机工程学报,2004,24(7):151-155.
[3] Takahashi I,Noguchi T.A New Quick-response and High Efficiency Control Strategy of an Induction Motor[J].IEEE Transaction on Industry Applications,1986,22(5):820-827.
[4] Zhong L,Rahman M F.Analysis of Direct Torque Control in Permanent Magnet Synchronous Motor Drivers[J].IEEE Transactions on Power Electronics,1997,12(3):528-536.
[5] Zhong L,Rahman M F.A Direct Torque Cont roller for Permanent Magnet Synchronous Motor Drivers[J].IEEE Transactions on Energy Conversion,1999,14(3):637-642.
[6] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.
[7] 韩京清.从PID技术到“自抗扰控制”技术[J].控制工程,2002,9(3):13-18.
[8] 冯光,黄立培,朱东起.采用自抗扰控制器的高性能异步电动机调速系统[J].中国电机工程学报,2001,21(10):55-58.
[9] 陈诚,李世华,田玉平.永磁同步电机调速系统的自抗扰控制[J].电气传动,2005,35(9):13-16.
[10] 夏长亮,李正军,杨荣,等.基于自抗扰控制器的无刷直流电机控制系统[J].中国电机工程学报,2005,25(2):82-86.

