在转子系统中利用共振法测量轴承的动态径向刚度
马会防 ,刘高进,南瑞民,戴哲峰
(1.上海凯泉泵业(集团)有限公司 技术中心,上海 201804;2.金华职业技术学院 机电工程学院,浙江 金华 321000)
转子系统中滚动轴承的刚度等参数特别重要。文献[1]研究了非均匀轴承游隙转子系统的动态响应和稳定性问题,文献[2-3]研究了轴承刚度对转子系统的动力学性能的影响,指出轴承刚度特性与其运行状态相关。
计算方面,以Hertz接触理论为基础,有的提出了简化公式,有的考虑了外载荷、游隙、油膜、预紧力及转速等诸多因素的影响[4-10]。由于影响轴承刚度的因素很多,导致计算值与实测值相差较大,所以,在关于计算方法的研究中,通常不采用计算值与实测值进行对比,而是不同计算方法之间的对比。
测试方面,一类是静态测试,基于Hooke定律,通过测量套圈相对线性位移得到轴承的刚度,这类方法对油膜、内外圈预紧变形等因素考虑的较少,测试结果是一种静态刚度,与轴承工作状态下的真实刚度有时相差很大。
还有一类是动态测试,一般采用轴承的非旋转直接激振法,通过施加已知的激励,测量振动响应来确定轴承的刚度[11-12],由于滚动体不是处于转动的工作状态,测试值也类似于静态刚度;文献[13]利用轴承共振的方法,在滚动体处于旋转状态时测得了轴承的动态刚度,但是轴承的外圈处于自由状态,轴承游隙大于实际工作状态;文献[14]从随机振动响应中提取了轴承的动态刚度参数,该测试模型基本上完全模拟了轴承的实际工作状态,然而,其把模型中的转子假设为刚性体,而转子应为弹性体,只有弹性体的刚度远大于轴承刚度时,才可以把转子理想化为刚性体。所以,它得到的结论之一:“转子的抗弯刚度大于轴承刚度时,测出的轴承刚度接近真实值”,就是假设与实际不符合导致的。
鉴于以上研究,提出了一种测试方法,在旋转的转子系统中,测量轴承的动态径向刚度,就是在轴承处于旋转的工作状态下,测算轴承的径向刚度。
试验的物理模型是支座-轴承-转轴系统,根据文献[14]中提到的振动模型简化原则,将物理模型简化为力学模型,其中,支座结构厚重,可以认为是刚性体;轴承主要起弹性支承作用,简化为弹簧;转轴则是同时具有质量、弹性和阻尼的模型。通过激发共振——变速电动机带动转子系统不断加速,越过一阶共振区,测出试验物理模型的一阶横向振动频率,再根据简化后的力学模型,计算出轴承的径向刚度。
1 转子系统模型与基本理论
1.1 转轴的力学模型
由于转轴的质量、弹性和阻尼没有明显差别,故需要把转轴简化为同时具有质量、弹性和阻尼的模型。
转轴物理模型的质心位于中部,所以,力学模型的质量也位于质心处;设转轴本身结构的质量为m,力学模型的质量设为等效质量me,一般me 转轴的物理模型为连续弹性体,由于试验过程中只测试系统的一阶横向振动,其振型简单,轴上各处同相振动,所以,转轴可以简化为无质量的刚性轴,以及支承处的等效刚度ke和等效阻尼ce,如图1所示。 图1 转轴物理模型与力学模型对比 实际上,上述过程是把转轴简化成了单自由度模型,等效质量、等效刚度及等效阻尼为单自由度模型的模型参数。这些模型参数的求解可通过有限元法求得,简述其过程,就是创建转轴的有限元模型,在支撑处添加刚性支撑弹簧,计算转轴的一阶横向振动频率;然后在质心处添加点质量,仅改变模型的质量,再次求解转轴的一阶横向振动频率;接下来,改变点质量并再次求解转轴的一阶横向振动频率。这样,根据单自由度模型与有限元模型之间的对应关系,就得到关于3个未知参数的3个方程,解方程就求得转轴的等效质量、等效刚度和等效阻尼,详细过程可查看转子单自由度模型参数的有限元解法,此处不加赘述。 轴承相对于转轴质量较小,且主要起径向弹性支承作用,所以简化为径向弹簧,刚度值为kb。 支座结构厚重,刚度值较大,可以认为是刚性体。具体刚度值可以根据Hooke定律进行实测,也可以建立有限元模型,通过静力分析求得。与最后求出的轴承刚度进行比较,如果支座在径向的刚度值远大于轴承的径向刚度值,则证明支座假设为刚性体是合理的。由于支座与地基相连,且是刚性体,所以,支座在力学模型中表示为地基。 基于以上模型的简化,转轴-轴承-支座系统可以表示为如图2所示的单自由度模型系统。 图2 简化后的单自由度转子模型 该转子系统模型的总刚度为 (1) 总阻尼为 c=2ce, (2) 固有频率为[15] (3) 式中:kb,ke分别为轴承、转轴的等效刚度,N/m;ce为转轴的等效阻尼,N·s/m。 设转子系统的一阶横向振动频率为f,在测试上其对应于转子的一阶临界转速[14],可通过Bode图直接测出,设测试值为N(r/min);在理论上其对应于单自由度力学模型的固有频率,因此 (4) 结合(1)~(4)式,可得轴承的径向刚度为 (5) 测试模型为一实际产品的转轴,按照生产装配要求,安装了NU315轴承,然后将转子系统安装在转子试验台上。测试模型如图3所示,主要包括转轴、轴承、支座、调速电动机和振动传感器(含有Bode图测试功能的振动测试系统)。 图3 试验装置简图 控制调速电动机,使其转速由静止均匀加速到3 500 r/min,测得临界转速N约为2 250 r/min,测得的Bode图如图4所示。 图4 测定临界转速的Bode图 转子质量为144 kg,三维CAD模型如图5所示。根据转子单自由度模型参数的有限元解法,利用一阶横向振动频率值与单自由度模型固有频率之间的对应关系,可得 图5 某型转子的CAD模型 (6) 通过在质心处添加和改变点质量的方法,可得到多个形如(6)式的关于me,ke和ce的方程,求解方程组即可。 具体过程如下: (1)在CAD模型中,求出质心坐标; (2)在CAE模型中,添加刚性弹簧支撑(弹簧刚度值1011N/m); (3)模态分析,根据一阶横向振型,判断出相应的频率f=60.134 Hz; (4)在质心位置,添加点质量Δm=0.5m=72 kg,重新计算,判断出一阶横向振型相应的频率,记为f1=40.718 Hz; (5)在质心位置,添加点质量Δm=m=144 kg,重新计算,判断出一阶横向振型相应的频率,记为f2=30.017 Hz; (6)将f,f1,f2代入(6)式,可求得图2所示转轴单自由度模型的参数,结果见表1。 表1 单自由度转轴模型的参数 将测得的临界转速N以及计算得到的转轴模型参数代入(5)式,可计算得出该轴承的动态径向刚度 kb=4 743 376.521=4.743 8×106N/m。 轴承径向刚度理论计算值的量级通常为107或108,而本次测试值比一般静态计算值偏低,其原因可能是该转子的轴承不需要预紧,安装后还是正游隙,且转轴的径向力基本为零;而转动时的油膜状态等诸多因素很难体现在理论计算中。因此,对于轴承的径向刚度,尤其在实际安装状态下的动态径向刚度,不宜用纯理论的方法估算,最好进行实测。 研究me,ke和ce的计算过程,发现与Δm/m关系比较大,结果如图6所示。 图6 参数计算结果的稳定性与Δm/m的关系 当Δm/m较大(lg(100Δm/m)>1.3,即 Δm/m>0.2)时,参数的计算结果稳定性比较好;当Δm/m较小(lg(100Δm/m)≤1.0,即Δm/m<0.1)时,计算结果稳定性较差,即参数me,ke和ce的计算结果可能与真实值偏差较大。 由于求解一阶横向振型时使用的是有限元法,计算结果与网格大小等有限元软件的相关设置也有关,但是由于有限元技术已经相当成熟,合理、正确设置的前提下,单元大小等有限元因素影响可以忽略。 对于参数N,测定Bode图时,可以通过提高采样频率、减小测定的转速范围等方法,更加精确地测定峰值对应的转速。 用上述方法测试轴承的动态径向刚度,需要转轴两端安装同样的轴承(组),而实际转轴可能在两端安装不同型号的轴承,这时,假设一端的径向刚度为kb1,另一端为kb2,则待求物理量为2个。 该问题的解决,可通过Bode图测试临界转速N,之后在转轴质心处加装轴对称质量块Δm,然后再测临界转速,设测得的临界转速为N′,则可以得到关于kb1与kb2的二元二次方程组,理论上可以求解。 之前的分析讨论中,一直忽略了轴承的径向阻尼,如果需要考虑,则待求物理量除了径向刚度kb,又添加了径向阻尼cb。 该问题同样可采用3.2节所述方法进行解决。 由于试验条件的限制,暂时无法通过试验求证3.1和3.2中的问题。 前面已经提到影响轴承刚度的多种因素,而游隙对径向动态刚度也有很大影响,可通过改变轴承预紧力而改变径向动态刚度。预紧方式有定位预紧、定压预紧。由于当前试验中的轴承没有预紧装置,不能进行不同预紧情况下轴承径向动态刚度的对比试验,但运用上述方法,将来可以进行这方面的研究和试验。 (1)通过简化物理模型,建立转子系统的力学模型,找到了轴承径向刚度与临界转速的函数关系,为进行动态径向刚度的测试奠定了理论依据。 (2)通过试验测定了某型号产品的轴承动态径向刚度,分析了动态径向刚度测试值和理论计算的不同,并探讨了影响动态径向刚度测量和计算结果的因素。 (3)讨论了转轴上装有不同型号的轴承时,如何测量动态径向刚度。 (4)分析讨论了轴承的径向阻尼问题以及理论上的解决方法等。
1.2 轴承与支座的力学模型

1.3 轴承径向刚度的计算公式
2 测试与计算
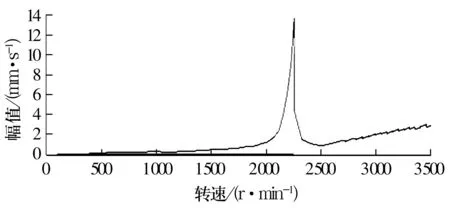
2.1 测试模型与测试结果

2.2 力学模型的计算


2.3 轴承径向刚度的计算
3 分析与讨论
3.1 影响计算结果的因素

3.2 不同型号轴承的动态径向刚度
3.3 轴承的径向阻尼
3.4 轴承预紧力对径向动态刚度的影响
4 结论

