基于ANSYS和iSIGHT的磁悬浮轴承结构优化设计

肖林京，张绪帅，常龙，郭海

(山东科技大学 机械电子工程学院，山东 青岛 266590)

主动磁悬浮轴承(AMB)是利用电磁铁产生的可调电磁力将高速转子无接触地悬浮于其轴心位置的一种新型轴承。与传统的机械轴承相比，磁轴承具有无接触摩擦、高速度、低功耗、高精度和无需润滑等优点，广泛的应用于交通、高速机床、航空航天等工业领域[1-2]。磁轴承性能的好坏虽然与控制系统的设计密不可分，但是机械结构选择同样对其有着至关重要的影响。磁轴承所能获得的最大承载能力由所使用的磁性材料的最大磁通密度所决定，为了增加电磁轴承的承载力，减小起重量和尺寸，有必要对磁轴承的结构进行合理地分析与研究，从而减少磁饱和现象对磁轴承性能的影响。文献[3-4]用有限元方法对磁轴承电磁特性进行了分析。但是随着设计变量的增多和外界因素的影响，需要解决管理和数据协调上的许多问题，传统的建模和分析方法已满足不了要求。

在此，采用能与有限元分析软件ANSYS无缝兼容的多学科优化设计软件iSIGHT[5]，可使设计过程简单而高效。在整个优化过程中，由于采用模块化的方法将ANSYS和iSIGHT结合，建立了一个参数可变的磁悬浮轴承模型，并实现了从建模到分析及优化的自动化，分析效率高，简便快捷，能够满足当前对分析和优化的要求。

文中以8极径向主动磁悬浮轴承为例，采用ANSYS对磁悬浮轴承建模和仿真，并在此基础上将参数及模型集成到iSIGHT中，对该模型进行了多目标优化，以得出该轴承结构的最优尺寸。

1 磁悬浮轴承的电磁场分析

由于文中研究的主动磁悬浮轴承是利用电磁力实现转轴的悬浮，因此在轴承的设计过程中，电磁力的计算过程尤为重要。目前对磁悬浮轴承电磁力计算主要有解析法和有限元法。

1.1 解析法

由于解析法中忽略了一些因素，导致结果与实际存在较大的误差，从而使得转子的受力特性和磁悬浮轴承的结构参数设计不够精确。因而只能作为辅助方法来参考计算。

1.2 有限元法

磁轴承工作在静态工作点时，可认为定子和转子间为静态场，列出电磁轴承系统的Maxwell方程组为[5-6]

(1)

(2)

B=μH，

(3)

引入矢量磁势A，使得

(4)

根据边界条件得

Az=Az0=0 (第一类边界) ，

(5)

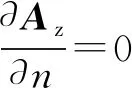
(6)

将(5)～(7)式联立，可以求出Az。有限元法就是把整个求解区域剖分成各个单元和节点，用上述方法求出各节点的矢量磁势A后，由(4)式求出每个单元的磁感应强度B的值。此时的B考虑了边缘效应和漏磁情况。

计算电磁力时可以通过对转子周围空气层的力进行求和，空气层单元q方向上力的基本公式可以表示为

(7)

(8)

式中：Wm为系统的磁场能量；v为单元体积。经过二维有限元离散化，(7)式可表示为

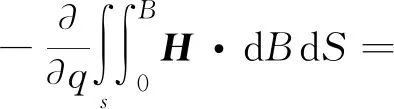
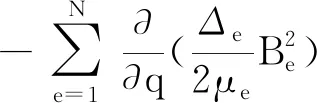
(9)

式中：e为单位号，e=1,…,N；S为离散的二维单元的面；Δe为单元的面积；μe表示单元相应的磁导率；Be表示单元的磁感应强度。

以上计算结果与试验结果非常吻合，有足够的正确性，因此采用有限元法来仿真磁悬浮轴承。

2 ANSYS对磁悬浮轴承的建模和仿真

采用APDL语言编写并建立参数化模型，使得磁悬浮轴承的参数可以方便调整，自动生成新的模型，为下一步iSIGHT的优化提供接口。

对于8极径向磁轴承(图1)，当转子处于轴承的几何中心时，上磁极对线圈进行加载。定子和转子采用无取向硅钢50W270叠压而成，其磁化曲线如图2所示，取饱和前允许的最大磁感应强度Bmax=0.8 T，线圈加载电流的大小由最大磁感应强度Bmax决定。轴承的初始结构参数包括可变参数和不变参数。可变参数为线圈槽的槽口高度H1=1 mm,槽口宽度H3=2.5 mm，磁极高度H2=10 mm，磁极宽度W1=10 mm；不变参数为定子外径R=65 mm，定子内径R1=25 mm，气隙G=0.3 mm，电流密度Jd=6 A/mm2。

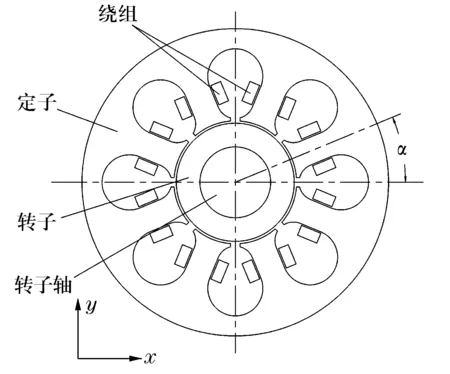
图1 8极磁悬浮轴承结构图

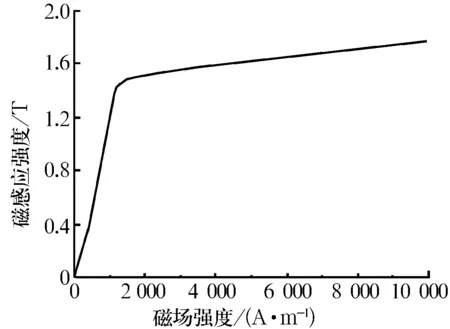
图2 50W270磁化曲线

在ANSYS中，首先进行几何建模，再经过网格划分并求解后，得到磁悬浮轴承的电磁场分布如图3所示，颜色越深代表磁感应强度越大。从图中可以看出磁场分布不均匀，磁感应强度最大的点出现在磁轭与磁极连接处。

图3 磁感应强度分布图

同时，从图4可以看出，磁悬浮轴承模型的磁力线大部分能按照预期的路线分布，具有对称性，但是回路中也存在一定程度的漏磁现象，因此有限元法得到的气隙磁感应强度会比解析法偏小，最终该分析模型得到的最大磁感应强度Bmax=0.827 8 T，Maxwell力Fyy=72.165 7 N，定子质量m=2.724 1 kg。

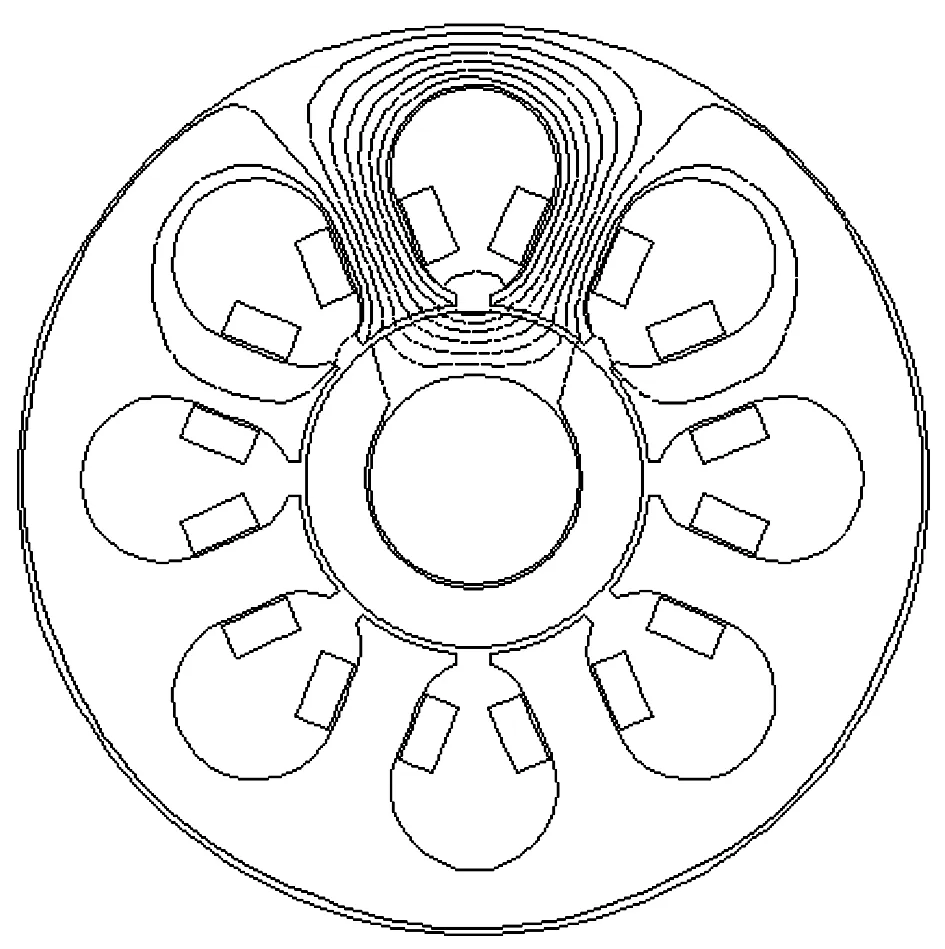
图4 磁力线分布图

3 iSIGHT优化分析

iSIGHT是一套可以整合设计流程中所使用的各项软件的工具，并且是一个能自动进行最优化设计的软件系统平台。它融合了设计优化中需要的3大主要功能：自动化功能、集成化功能和最优化功能。iSIGHT的这种特性使得产品的设计周期缩短、产品成本降低和品质提升。传统的优化方法是利用建模工具建立所需要的模型，然后导入分析软件，进行产品分析。而文中通过对iSIGHT和ANSYS的集成，可以针对不同的问题，且可以任意嵌套和组合各种算法，从而通过智能化的探索，选择新的设计出发点，进而仿真和优化，实现过程的自动化。在每次循环过程中，可以实现实时监控，而且设计的参数输入和输出可以在执行过程中显示，方便控制。

3.1 数学模型的建立

在此，主要研究磁悬浮轴承在提供足够大的电磁力(文中为70 N)和磁感应强度不饱和的条件下，定子质量的最小化。因此问题就可以描述为如何设计轴承的参数，使得轴承能在满足约束的条件下实现最优化，节约成本。

对于文中模型可表示为

Minmizem(X)，

s.t.0.6≤Bmax(X)≤0.8，

70 N≤Fyy(X)

式中：Minimize代表向量的极小化，也就是向量目标函数组中各个目标函数都尽可能达到最小化。s.t.为约束条件。即找到最优的X使得在满足约束的条件下得到最小的质量。

3.2 iSIGHT和ANSYS的集成优化

图5所示为iSIGHT优化流程图，ANSYS通过编程集成到iSIGHT中，采用批处理方式运用脚本命令驱动ANSYS软件进行分析，然后读取输出文件，利用iSIGHT自身优化算法进行设计参数修改，修改后的设计变量返回分析的输入文件，然后再传递给ANSYS进行下一步运算。

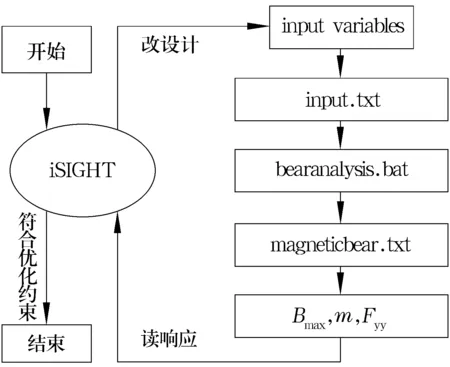
图5 iSIGHT优化流程图

本例的iSIGHT主要包括以下几个文件：input.txt，magneticbear.txt，bearanalysis.bat，isight.desc。各文件的主要功能和作用如下所述。

(1)bearanalysis.bat调用一个用ANSYS语言编写的APDL文件，用于从输入文件中读取磁悬浮轴承的参数，然后在ANSYS中进行模型的调用和仿真；同时将ANSYS计算结果写入到输入文件input.txt中，以便iSIGHT下一次的优化调用；

(2)input.txt，magneticbear.txt为系统的输入输出文件，储存每次仿真的模型变量数值；

(3)isight.desc为iSIGHT工程文件，与ANSYS集成后生成，是系统的执行文件。

ANSYS集成到iSIGHT中的操作界面如图6所示，在优化过程中采用NLPQL数值优化算法。NLPQL通常用来解决带有约束的非线性数学规划问题，并假设目标函数和约束条件是连续可微的。二次连续规划法(SQP)是NLPQL的核心算法。将目标函数以二阶Taylor级数展开，并把约束条件线性化，原非线性问题就转化为一个二次规划问题，通过解二次规划得到下一个设计点；然后根据2个可供选择的优化函数执行一次线性搜索。优化过程中目标函数质量、最大磁感应强度及最大电磁力的变化如图7～图9所示。

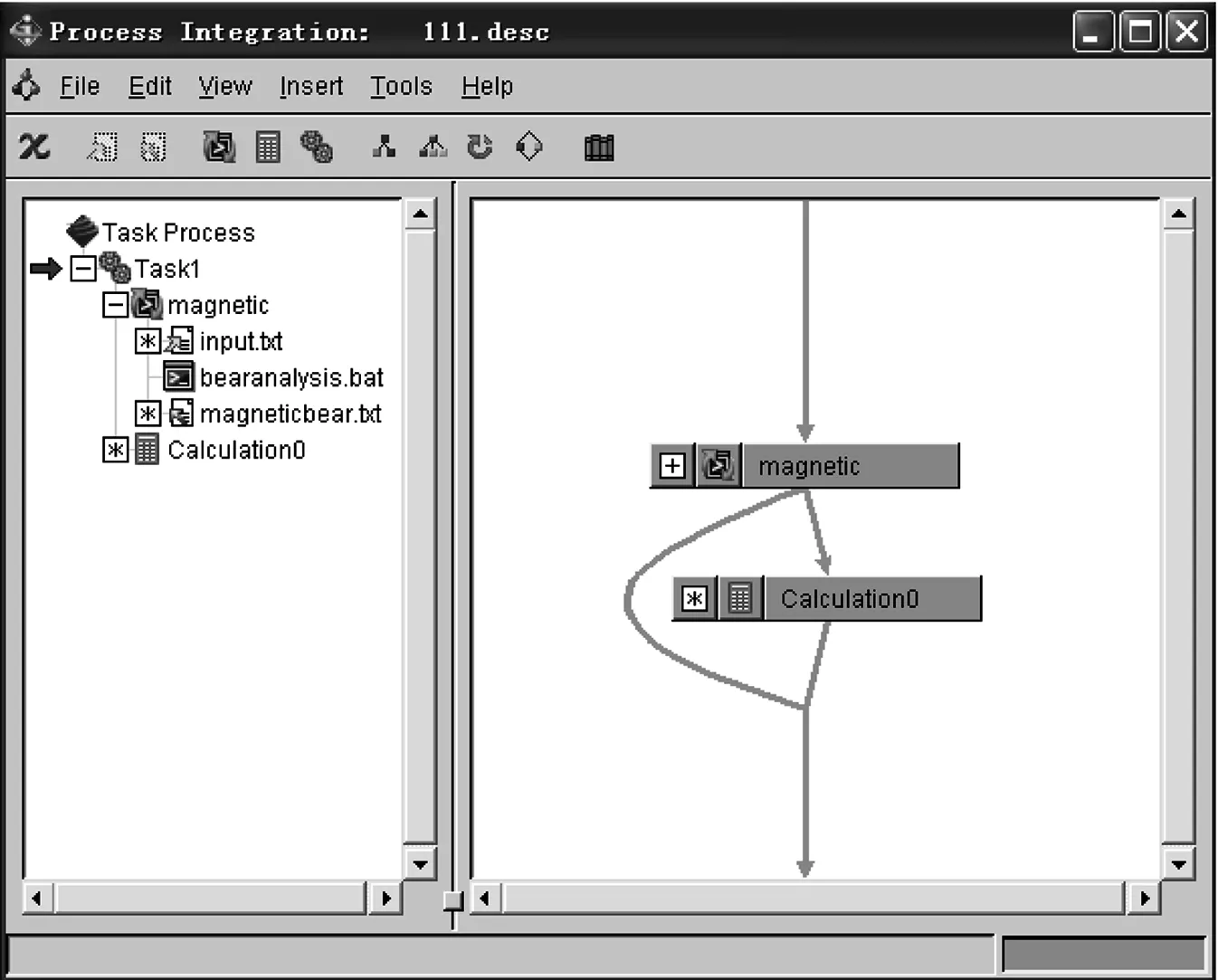
图6 集成界面图

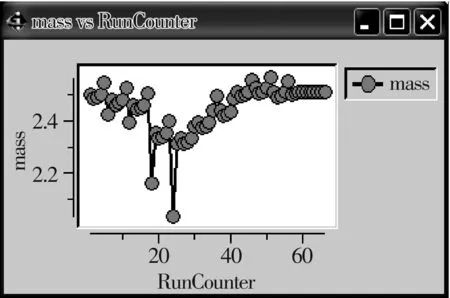
图7 质量优化过程图

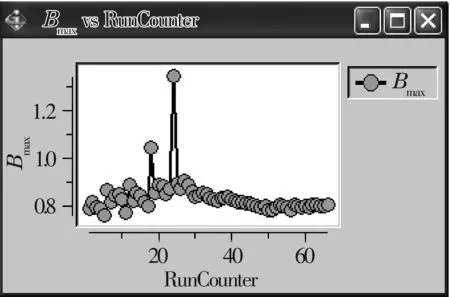
图8 最大磁感应强度优化过程图

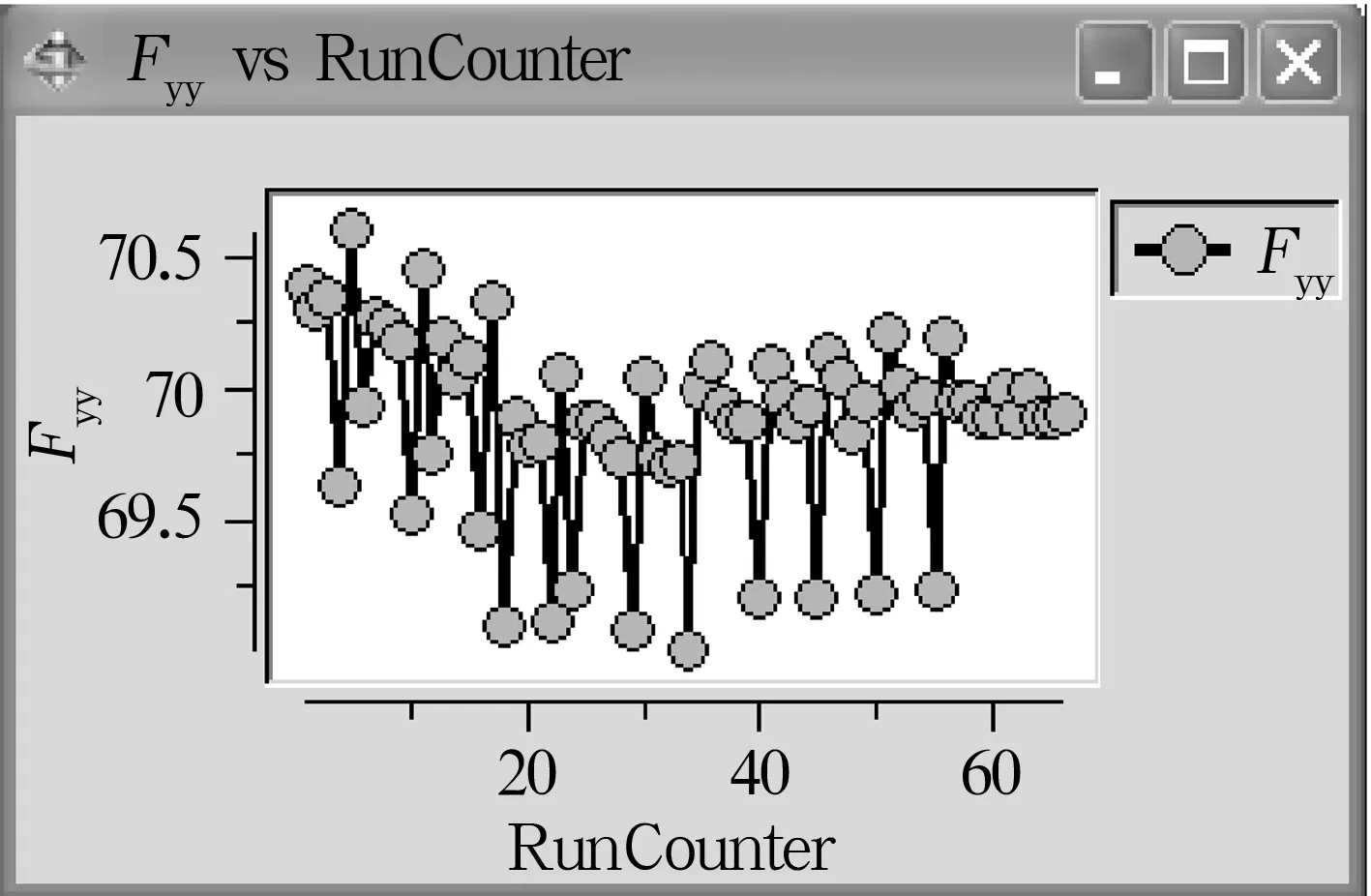
图9 最大电磁力优化过程图

3.3 优化结果

该模型的优化结果见表1，可以看到轴承槽的参数得到了改善，优化后在电磁力Fyy≥70 N，磁感应强度0.6 T≤Bmax≤0.8 T的条件下，得到了磁轴承的质量m为2.487 590 kg，相比于优化前，质量减轻了8.7%，满足优化的要求。

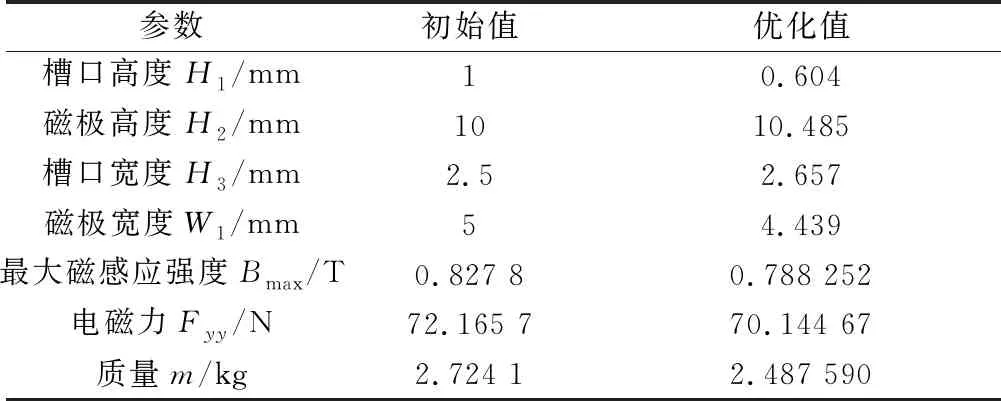
表1 轴承的优化结果

4 结束语

为主动磁悬浮轴承建立了相应的模型并得到了轴承的磁场分布情况，且成功地利用优化平台iSIGHT集成有限元软件ANSYS对轴承的结构进行了轻量化优化设计，得到了满足要求的模型参数。该方法大大减少了重复工作，提高了设计效率、质量以及自动化程度，具有收敛速度快，稳定性和可靠性高等优点；并且为类似产品的设计开发提供了一套系统的方法和参考。