长度计量基础知识讲座(三十六)
/上海市计量测试技术研究院
第三十六讲 测绘概况
1 测绘工作的主要内容
测绘离不开测绘仪器。作为用于国家土地规划、工程建设、国防与地震监测等的各种测绘仪器如水准仪、经纬仪、测距仪、全站仪和GPS等是测绘过程中不可缺少的计量器具。在介绍测绘仪器之前,简单介绍测绘工作的主要内容。
测绘学是研究和确定地面和空间的点位相对位置的科学。它的内容一是将地球上的地貌、地物、行政和权属范围测绘成图或构成数字模型;二是将规划和建筑设计的点和线在实地定位。按测绘研究和应用的重点范围分类,可分为以下几门主要学科:
1.1 大地测量
研究和测定地球表面广大地区的点的定位及地球的形状、大小和地球重力场。
1.2 地形测量
研究和采集地表局部地区的自然地貌、人工建筑及权属界线等测绘成图或形成数据库。
1.3 工程测量
研究工程建设在设计、施工和管理阶段中进行测量工作的理论、技术和方法。
1.4 摄影测量
研究利用摄影或遥感手段获取地物和地貌或某构筑物的影象和光谱,进行分析和处理以确定其形状、大小和位置,绘制成图或提供数字文件。
2 地球的形状和大小
人们在地球上进行建设和测量作业,必须了解地球的形状和大小。利用测绘仪器确定地面和空间点位的坐标系。
地球自然表面极为复杂,有高山、深谷、丘陵、平原和河川、海洋等。其中海洋占整个地球表面的71%,而地球上最高的珠穆朗玛峰8 844.43 m,最低的马里亚纳海渊在海面下11 022 m,这些高低起伏相对于地球半径(6 371 km)来说是很小的。于是地球总的形体可设想成一个处于静止状态的平均海水面延伸穿过陆地所包围的形体。海洋或湖泊在自由静止时的表面,称为“水准面”。水准面是受地球重力影响而形成的。受涨、落潮的影响,水准面有无数多个,其中与平均海水面相吻合的水准面称为“大地水准面”。水准面是一个处处与铅垂线方向垂直的曲面。由于地球内部质量分布不均匀,使铅垂线方向引起变动,致使大地水准面成为一个略有起伏而不规则的复杂曲面。在该曲面上无法进行测量结果计算。为此,人们就选用一个非常接近大地水准面,并可用数学式表示的旋转椭球面来代替它,表示地球总的形状。它是一个椭圆绕其短轴旋转而成,其旋转轴与地球自转轴重合,称为“总地球椭球”,简称“总椭球”,见图1。事实上,全球统一的与整个地球的大地水准面密切配合的总椭球也很难精确求定,因为在占全球2/3的大洋面上很难取得相关的精确资料。所以各国只能采用与本地区大地水准面密切配合的椭球面,作为测量计算的基准面。称这种椭球为“参考椭球”。因此总椭球应只有一个,而参考椭球则有多个,各国不尽相同。
决定椭球体形状和大小的元素为椭圆的长半径a、短半径b。并由此可算出另一个参数:偏率f;其关系式为
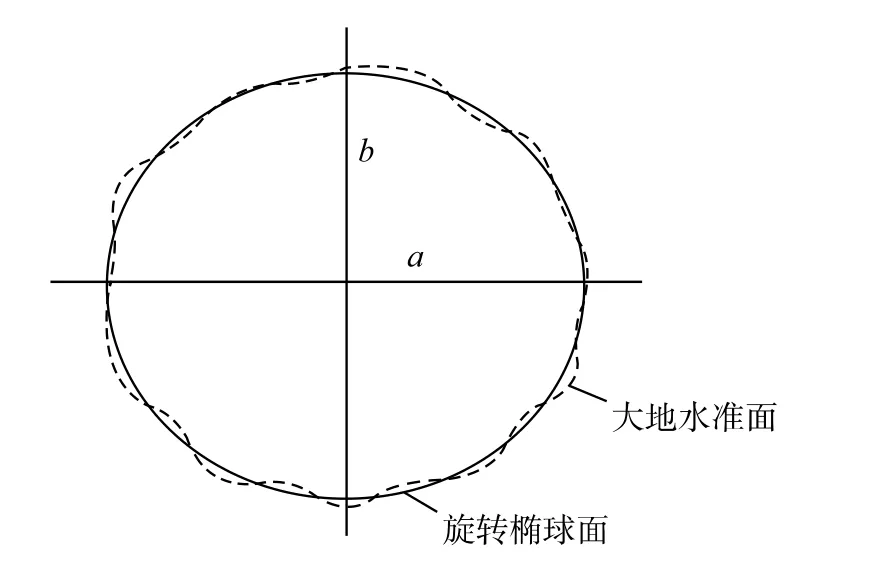
图1 总地球椭球

我国所采用的参考椭球元素为
a=6 378 137 m,b=6 356 752,f=1/298.257
地球参考椭球体面是本国大地测量投影和计算的基准面。由于地球椭球体的偏率很小,故当测区较小时,可把地球当作圆球看待,其半径可取:R=(2a+b)/3,其近似值为6 371 km。
3 确定地球面上点位的几种坐标系
地面点的空间位置,通常可用该点相对于某基准面和基准线的三维坐标或二维坐标来确定。确定地面点空间位置的几种坐标系如下。
3.1 地心坐标系
是以总椭球为根据的空间三维直角坐标系,是一个世界统一的理想地心大地坐标系,用于卫星大地测量。
3.2 地理坐标系
是采用以大地水准面和参考椭球为根据的球面坐标系,按投影面的不同,分为天文坐标系和大地坐标系。
3.2.1 天文坐标系
天文坐标又称天文地理坐标,是用天文经度λ和天文纬度φ来表示地面点投影在大地水准面上的位置。
国际公认通过英国格林尼治天文台的子午面为首子午面,作为计算经度的起始;并规定自首子午线向东或向西计算,都为0°至180°称为东经或西经。垂直于地轴的平面与球面的交线称为纬线。垂直于地轴并通过地球中心的平面为赤道平面,其与地球面相交的线为赤道;某A点的纬度,即为该点的铅垂线与赤道平面的交角。赤道是纬度的起始线,自赤道向北或向南,都为0°至90°称为北纬或南纬。
各点的天文坐标(λ,φ),是在各点上用天文测量法独立测定的。例如北京某点的λ为 东经116°28',φ为 北纬 39°54' 。
若再顾及地面点超出大地水准面的垂距(海拔高h),那就构成为三维坐标系(λ,φ,h)。
3.2.2 大地坐标系
大地坐标又称大地地理坐标,是用大地经度L和大地纬度B表示地面点投影在参考地球椭球面上的位置。A点的大地经度L,就是包含A的大地子午面与首子午面所夹的两面角;A点的大地纬度B,是过A的椭球面法线与赤道平面的交角。各点大地经、纬度的确定方法与天文经、纬度测定的方法不同,它们是根据一个起始的大地点(称为“大地原点”,该点的大地经纬度与天文经纬度一致)的大地坐标,再按大地测量所得的数据推算而得到的; 这是传统的方法。
我国的大地原点设立在陕西省泾阳县,作为全国大地坐标的起算点;由此建立的大地地理坐标系称为“1980国家大地坐标系”。
地面点超出参考椭球的垂距称为“大地高H”。若再顾及大地高之值,那也就成为三维坐标(L,B,H)。
近代卫星大地测量的发展,将更多地用GPS方法获得测点地心坐标系的空间大地直角坐标。经过坐标转换,也可获得该点的大地地理坐标L,B,H之值,或其他应用的坐标系统中之值。相对于传统的方法,可以说是一大飞跃。
3.3 平面直角坐标系
上述的地理坐标系或地心坐标系一般适用于确定高级控制点的定位或作为初始的计算。对于地球上大量的测量、工程放样、计算和绘图的工作,则最好是在平面上进行。但地球表面是一个曲面,要把在球面上所测的点位换算到平面上,对全境及大区域而言,就关系到投影的问题。
3.3.1 高斯平面直角坐标
用高斯投影方法把在球面上所测的点位投射归化到平面上所建立的平面直角坐标系。我国采用高斯投影方法。
3.3.2 地区平面直角坐标
对于局部的小区域,例如某个小城镇或施工地区,相对地球半径,这小块球面可以当作平面看待。可用测区中心的切平面P来代替大地水准曲面,此时在球面上实测的长度D也就不必顾及投影的变化当成是平面上的测量值,直接用于绘图或计算。
4 地面点的高程
由高程基准面到地面点的铅垂距离(高度),称为该点的高程。若高程基准面是大地水准面,则称为“绝对高程”或“海拔”。我国由青岛验潮站经多年观察所确定的“黄海平均海水面”作为大地水准面,其高程为零。为此,国家在青岛一个稳固的山洞里设置了“国家水准原点”,测得该点到黄海平均海水面的高度为72.260 m,即青岛国家水准原点的高程为72.260 m。全国性统一的绝对高程系,就是从青岛国家水准原点出发建立的。
在局部地区,为工程设计及施工放样的方便,有时就设定某个高度的水准面作为该地高程基准面,由此所得的高程值称为“相对高程”或称“假定高程”。
地球曲率对于投影到水平面上距离的误差影响,在半径为10 km的测区范围内是可以忽略的。那末地球曲率对于高差测量的误差影响又如何呢?以水平面代替地球水准面而产生的高程误差以Δh表示,则
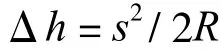
式中:s— 地面上距离;
R— 地球平均半径(R= 6 371 km)。由此可知,当s为1 km时,其高差误差Δh就会有8 cm。从而,在小区域对点的平面位置测量时可不顾及地球曲率的影响,但进行点的高程测量时,对于地球曲率的问题是常常要顾及的。

