一类耦合方程组弱解存在性证明

旷雨阳，陶从江

(贵州省安顺学院数计系，安顺 561000)

1 引言

偏微分方程是数学学科中的一个极其重要的领域，它是数学与其他科学学科联系的重要桥梁之一，也是基础数学发展的基本源泉之一，这主要是因为偏微分方程经常出现在物理学、工程技术和其他科学的许多分支之中。由于这一领域学科背景的多样性和复杂性，人们对这些偏微分方程已经作了广泛而且深入的研究(见文献［5］［6］)。

因此研究偏微分方程的方法很多，本文介绍一种研究偏微分方程组的解的存在性的重要方法，即schaulder不动点定理方法。这种方法在研究微分方程的解存在性有着广泛的应用(见文献［3］)。

2 预备知识

定理1.1.1(schaulder不动点定理):设C是赋范线性空间X中的一个闭凸子集，T:C→C连续，且T(C)列紧，则T在C上必有一个不动点。

定理1.1.2(schaulder不动点定理推论):设C为赋范线性空间中一个有界闭凸子集，T:C→C是紧的，则T在C上必有不动点。

3 假设条件:

H(3，1)，假设 a(x，t)是 QT中是测量函数，并且存在两个正常数 a0≤A0，满足:0 ＜ a0≤a(x，t)≤A0＜∞，对于 a，e，(x，t)∈QT，且 a(x，t)∈C1()H(1，2);假设∈

H(3，2)，假使 k(u)与 r(u)是 C1+a(Ω)函数，且存在二常数0 ＜a0≤A0，满足:0 ＜a0≤r(u)≤A0＜∞，对于 a.e，(x，t)，且 k(u)≥a0，假设 u0(x)∈(Ω)，且|▽ ×∈L2(Ω)，

H(3.3)，假设 u0(x)≥0，a(x，u)关于 u一致 Lipschitz连续函数

4 耦合方程组弱解存在性证明

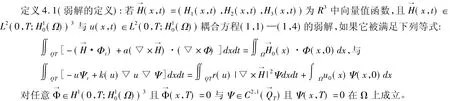
定理4.2:在假设 H(3，1)—H(3，3)条件下，耦合方程组(1，1)—(1，4)有一整体弱解。

证:为了简单，我们取k(u)=1，其他一般情况可类似地得出，为了得到所需要的结论，我们使用schaulder不动点定理，先假设 T 是任意固定的数，并设 k={u(x，t)∈L1+ε0(QT)‖u‖L1+ε0(QT)≤k0}，这里ε0∈(1，2)是固定的数，k0是后面被指定的数，对任意V(x，t)∈k，我们考虑下列发展系统:

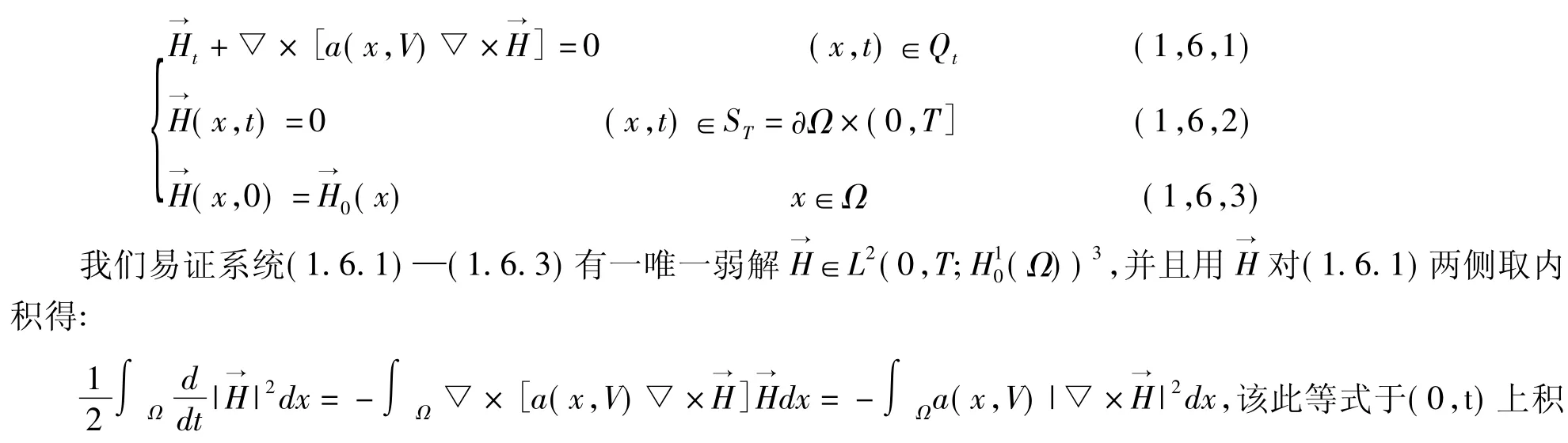
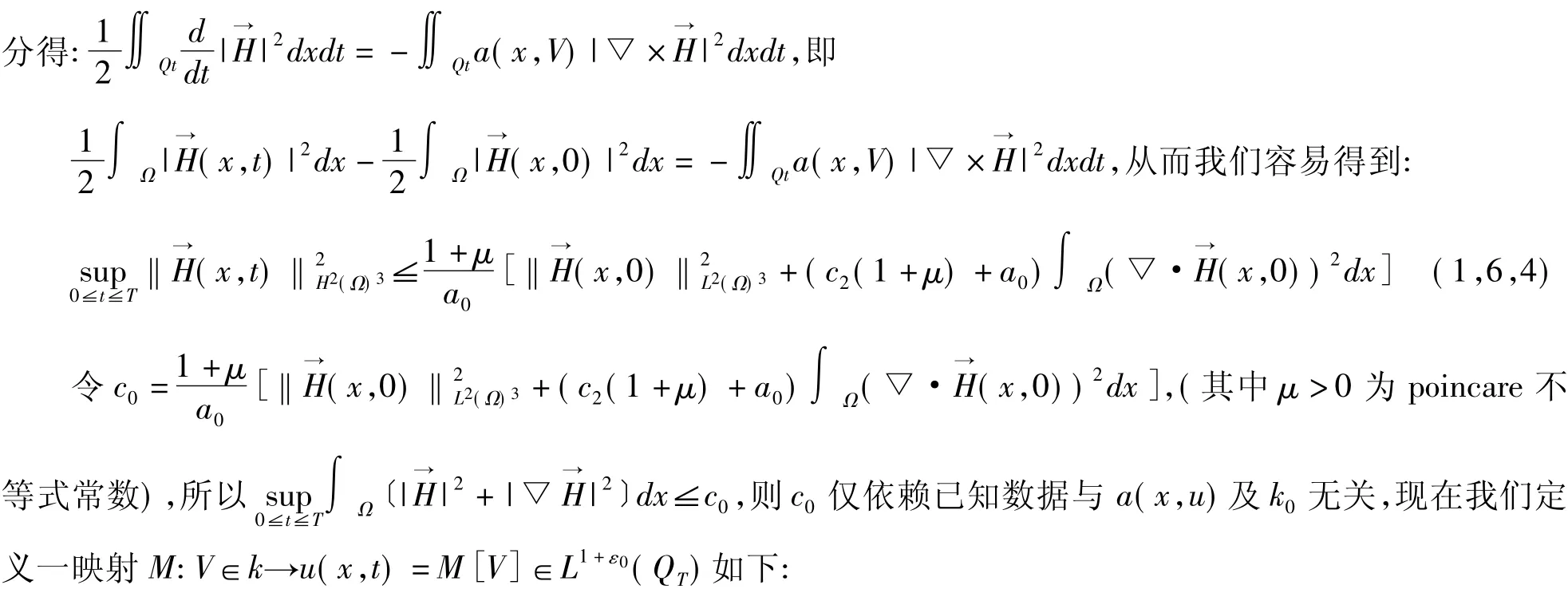
对每一V(x，t)∈k，我们定义M［V］=u(x，t)是下列抛物方程的弱解:

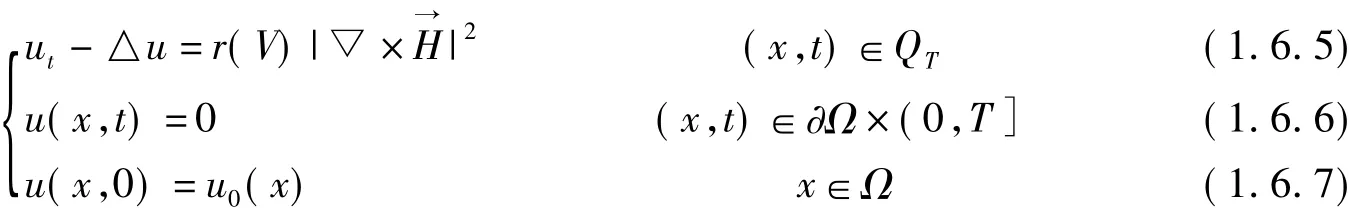
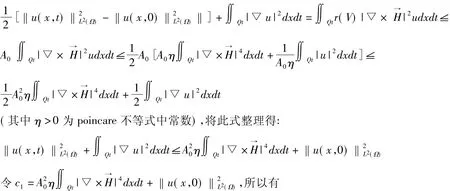
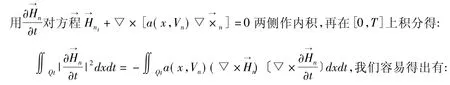
［1］伍卓群，尹景学，王春朋.椭圆与抛物型方程引论［M］.北京:科学出版社，2003

［2］陈恕行，洪家兴.偏微分方程近代方法［M］.上海:复旦大学出版社，1988

［3］张恭庆，林源渠.泛函分析讲义［M］.北京:北京大学出版社.1986

［4］D吉尔巴格，NS塔丁格.二阶椭圆型偏微分方程(中译本)［M］.上海:上海科学技术出版社，1981

［5］郇中丹，黄海洋.偏微分方程［M］.北京:高等教育出版社，2004

［6］Tyn Myint－U.数学物理中的偏微分方程［M］.徐元钟译.上海:上海科学技术出版社，1983

［7］Pierre － Louis Lions.Mathematical topics in fluid mechanics(volume 1.incompressible models)［M］.Clarendon press，Oxford:1996

［8］Eduard Feireisl.Dynamics of viscous compressible fluids.Mathematical institute of the academy of sciences of the Czech republic［M］.Oxford:university press，2004

［9］ Terence Tao.Nonlinear Dispersive equations:local and global analysis.Department of mathematics［M］.UCLA.LOS:Angeles.CA.90095.1991