仿水黾模型承载力试验研究

王庆成，杨晓东，曹国华，徐洪吉

( 1.长春理工大学 机电工程学院，长春 130022；2. 吉林工程技术师范学院 机械工程学院，长春 130052；3. 长春工程学院 机电工程学院，长春 130021)

0 引言

水黾一种是生活在池塘等水域的昆虫，它高超的水面滑行技能和超大水面承载力引起了人们浓厚的兴趣，成为世界各国科技工作者争相研究的热点问题之一[1～3]。江雷等[4]认为水黾的超大承载力是由其腿部特殊微纳米结构导致的超疏水效应实现的，并测出水黾单条后腿的最大承载力是其体重15倍，接触角是167°。受水黾腿部超大承载力的启发，一些学者对超疏水表面的承载力进行了研究。张希等[5]对金丝表面进行化学修饰，当金丝表面的接触角为150°时直径为1mm金丝仍会漂浮在水面；潘钦敏等[6]用直径为20mm的超疏水圆形铜箔作为水黾模型腿部，发现承载力与铜箔的接触角等因素有关。

本文通过力学分析，建立仿水黾模型的承载力模型，并试验验证所建承载力模型的准确性。

1 承载力模型的构建及分析

1.1 承载力数学模型的构建

将仿水黾模型置于水面时，其腿部在水面压出水涡。仿水黾模型的腿部为圆柱体，其横截面受力情况如图1所示。

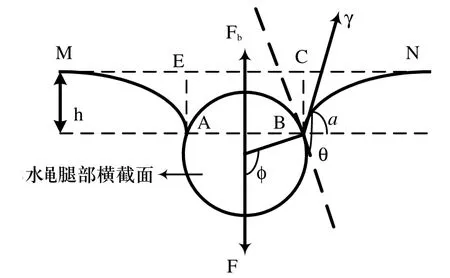
图1 仿水黾模型腿部力学分析示意图

图1中虚线MN代表水平面，A与B为仿水黾模型腿部与水面接触的边界点。仿水黾模型腿部在水面受到三个力作用，压力F、表面张力g和浮力Fb。浮力方向竖直向上，可通过对仿水黾模型腿部与水接触区域的静力学压力积分求出[7,8]，其等于图1中虚线所绘矩形ABCE的排水量，由于仿水黾模型腿部直径（0.45mm）较小，近似等于线段AB长度。所以仿水黾模型腿部浮力（Fb）的表达式为

式（1）中r为水的密度，g为重力加速度，h为水涡深度，D为仿水黾模型腿部直径，L 为仿水黾模型腿部长度。

表面张力方向为液-气界面上点B的切线方向， 其竖直分量（Fs）表达式为

式（2）中g为表面张力常数，a为液-气界面上点B的切线与水平线夹角。表面张力竖直分量通过对仿水黾模型腿部与水接触区域的曲面压力积分求出[7,8]，其等于图1中AME和BCN两个区域的排水量。

由于仿水黾模型腿部在水面压出水涡的两侧是对称的，表面张力的水平分量是平衡的；在竖直方向上，仿水黾模型腿部承受压力、浮力和表面张力竖直分量作用，它们是平衡力。仿水黾模型腿部的承载力（F）的表达式为

由（3）式可以看出仿水黾模型腿部的承载力由表面张力竖直分量和浮力组成。其承载力与L、h、a、D、g、r、g等因素有关。r、g、g是环境参数，L、D是仿水黾模型腿部的参数，h、a是水涡参数。由图1得出 的表达式为

式（4）中j为仿水黾模型腿部润湿部分的半圆心角，q为仿水黾模型腿部的接触角。

1.2 刺破水面的临界条件

仿水黾模型取得最大承载力时，就是其腿部刺破水面的临界条件。表达式（3）中只有L与D为仿水黾模型腿部参数，取仿水黾模型腿部接触水面的一段L=1mm，直径D=0.45mm，g=9.8N/kg，r=103kg/m3，g=72.8N/m。依据文献 [9]得到a与h的关系表达式

依据表达式（1）、（2）、（3）、（5），取a在 0 ～p之间，由软件Matlab计算得到仿水黾模型腿部的浮力Fb、表面张力竖直分量Fs、承载力F随a变化的关系曲线如图2所示。Fb与a的关系近似是线性的，Fs与a的关系近似为抛物线。由于Fb在承载力中所占的比重较小，Fs在承载力中所占的比重较大[10]。当a=p/2时，仿水黾模型腿部承载力取得最大值。由表达式（5）知，此时水涡深度h=3.85 mm。

图2 Fb、Fs与F随a化的关系曲线

2 承载力试验

2.1 仿水黾模型的制作

制作仿水黾模型，如图3所示。仿水黾模型的躯干由铜片制作，腿部由铜丝制作，其体长为45.6mm，体宽为6.8 mm，自身质量为925.6mg。仿水黾模型有4条退，腿部直径为0.45mm，每条腿的长度为28.2mm，其中直立部分长度为10.0 mm，水平部分长度为18.2mm，同侧腿部间距为30.2 mm。

图3 仿水黾模型

2.2 仿水黾模型腿部的制备

铜表面的超疏水制备方法有许多，简单而实用的方法之一是先将铜表面粗糙化，再用氟硅烷等低表面能材料进行化学修饰。

本次试验所用铜丝直径为0.45mm，从上海国药集团化学试剂有限公司购买，试验的步骤为：

1）将铜丝浸入丙酮溶液中浸泡2分钟，去掉铜丝表面的杂质，再用纯净水洗净，晾干；

2）将铜丝投入到20mm的硝酸银溶液中浸泡20秒后取出，先用纯净水洗净，后用鼓风干燥箱（JC101型，上海成顺仪器公司产品）烘干；

3）将铜丝放置在电子显微镜（S-3000N型，Hitachi公司产品）下观察，发现铜丝的部分表面沉积了一层银条，银条的形状类似羽毛，长度约7μm，宽度约2μm；

4）把铜丝浸入到预先水解的浓度为1.0wt.%的C8F13H4Si(OCH2CH3)甲醇溶液中，在室温下浸泡1小时后取出，放入恒温干燥箱（202-3AB型，天津泰斯特公司产品），在130°C的温度条件下加热1小时。

经过上述处理后，用接触角测量仪（DSA100型，KRUSS公司产品）测量，铜丝表面的接触角为154°，实现了超疏水功能。

2.3 仿水黾模型的承载力测量

将仿水黾模型轻轻放置装满水的烧杯中，发现它能漂浮在水面，如图4所示。待其稳定后用镊子向其背部添加沙粒，直到仿水黾模型的腿部刺破水面，沉入水中。取出浸入水中的沙粒，烘干后的沙粒质量为166.9mg，加上仿水黾模型自身质量925.6mg，仿水黾机器人承载的总质量为1092.5 mg，即10.7 mN。

图4 漂浮在水面的仿水黾模型

把表1中的数据与r、g、g等参数代入表达式（3），计算得到仿水黾模型一条腿的最大承载力为2.96mN，因为仿水黾模型有4条腿，其最大承载力为一条腿的4倍，即11.8mN。

表1 计算仿水黾模型腿部承载力的相关参数

2.4 仿水黾模型承载力误差分析

仿水黾模型承载力的实测值与依据所建承载力模型的计算值的误差为1.1mN，此误差值与计算值的比率为9.3%。

仿水黾模型承载力实测值小于计算值的原因有两点，一是测量仿水黾模型承载力时，其腿部压出水涡的最大深度可能小于计算出的最大深度（3.85mm）；二是仿水黾模型自身的平衡问题，在向仿水黾模型背部添加沙粒的过程中，很难保证其完全处于平衡状态，进而可能由于瞬时偏载导致模型尚未达到最大承载力前，其腿部就已经刺破水面。

3 结论

1）本文建立了仿水黾模型的承载力模型，分析了仿水黾模型腿部刺破水面的临界条件，即a=p/2。

2）通过试验测量了仿水黾模型的最大承载力，与所建承载力模型的计算值相比较，误差值为1.1mN，误差率为9.3%。

3）该研究能为水面微型设备的承载力设计提供理论依据。

[1] Caponigro M A, Erilsen C H. Surface fi lm locomotion by the water strider, gerris remigis[J]. The American Midland Naturalist, 1976, 95(2): 268-278.

[2] Michael Dickinson. Animal locomotion: how to walk on water [J]. Nature, 2003, 424: 621-622.

[3] David L. Hu, Brian Chan, John.W.M. Bush The hydrodynamics of water strider locomotion[J].Nature,2003, 424 (6949): 663-666.

[4] Gao Xuefeng, Jiang Lei. Water-repellent legs of water striders[J]. Nature, 2004, 432: 26-26.

[5] Shi Feng, Niu Jia, Liu Jianlin, et al. Towards understanding why a superhydrophobic coating is needed by water striders[J]. Adv. Mater. 2007, 19: 2257–2261.

[6] Pan Qimin, Liu Jia, Zhu Qing. A water strider-like model with large and stable loading capacity fabricated from super hydrophobic copper foils[J]. Applied Materials Interfaces, 2010, 2(7): 2026-2030.

[7] DominicVella,Duck-GyuLee and Ho-Young Kim. The Load Supported by Small Floating Objects[J]. Langmuir 2006, 22, 5979-5981.

[8] Liu Jianlin, Feng Xiqiao, Wang Gangfeng .Buoyant force and sinking conditions of a hydrophobic thin rod fl oating on water[J].Physical Review E, 2007, 76: 066-103.

[9] 王淑慧, 吴立成. 水上行走机器人腿部静力学分析[J], 北京航空航天大学学报, 2010, 36(10): 1176-1179.

[10] Wang Qingcheng, Yang Xiaodong, et al.. Modeling and analysis of the supporting force of water strider’s legs.Applied Mechanics And Mechanical[J], 2011, 138-139:356-361.