基于窗函数的NLFM波形设计及脉压性能分析
贠亚男, 张文希,许明圣
(1. 平顶山工业职业技术学院,平顶山 467001;2. 长沙学院 电子与通信工程系,长沙 410003;3. 河南平高电器股份有限公司,平顶山 467001)
0 引言
线性调频(LFM)、相位编码以及非线性调频(NLFM)是现役脉冲压缩体制雷达中常用的脉压波形[1-2]。其中,线性调频和相位编码波形在匹配滤波器输出端具有较高的旁瓣,实际应用中尽管可通过加权处理降低旁瓣影响,但会造成压缩波形的主瓣展宽以及信噪比损失。而NLFM波形则无需进行加权操作,可通过设计和改变发射信号的频谱特征,在匹配滤波压缩输出端获取较低旁瓣的同时,能够有效避免因加权处理而引入的信噪比损失,在雷达和声纳等信号处理领域具有较好的应用前景[3~7]。基于窗函数的波形综合法是NLFM波形的主要设计方法[5],本文通过分析和对比几种基于经典窗函数设计的NLFM波形的脉压性能,得出了一些有益的结论,为NLFM波形的实际应用提供参考。
1 NLFM波形设计方法
设NLFM波形具有如下表达形式:


式(3)中w(f) 即为窗函数,根据一维距离模糊函数的方法并运用驻留相位原理得:
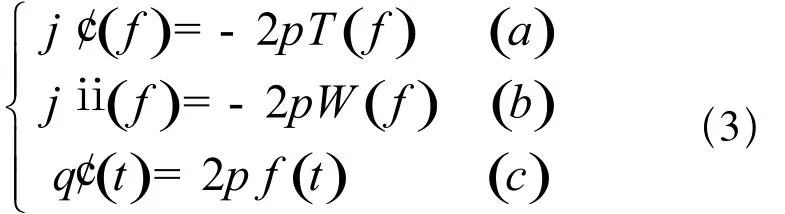
其中,T(f)为群延时函数,而f(t)则为信号频率,系群延时函数的反函数,即f(t)=T-1(f)。
基于窗函数设计NLFM波形需要首先确定窗函数W(f),其次通过式(3.b)求出j"(f),进而积分求出j'(f),再由式(3.a)得到群延时函数T(f),然后经反函数运算得到f(t),最后代入式(3.c)经积分得到相位函数q(f),最终获得NLFM波形m(f)。
2 典型窗函数及脉压分析
2.1 典型窗函数及群延时
1)矩形窗
矩形窗函数也称为门函数,对应了LFM波形的设计,其可表示为:
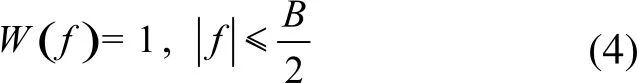
其中,B为信号的调制带宽,其群延时函数为T(f)=f。
2)海明窗
海明窗函数为:

3)余弦四次方窗
余弦四次方窗函数以及对应的群延时函数可分别表示为:

4)高斯窗
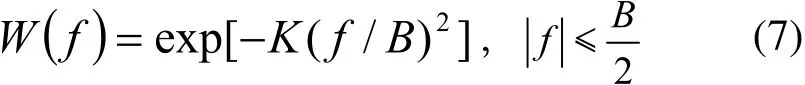
高斯窗函数一般表达式为:式中, K为常数因子,其群延时函数为T (f) = 2B/函数。
2.2 脉压分析
本节抛开冗长的脉压公式推导,利用信号与线性系统的基本知识理解脉冲压缩。矩形窗的频谱对应的是辛格函数,即:
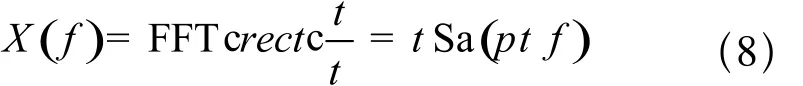
其中,rect和FFT分别表示矩形函数和傅里叶变换,而Sa(×)为辛格函数。
由式(3)可知,不考虑多普勒频移时,脉压时接收信号与参考信号在频域共轭相乘后,其相位谱可近似为一常数,幅度谱则对应窗函数,即NLFM信号脉冲压缩时的频域具有窗函数形式W(f )。因此,脉压最终归结到对窗函数的逆傅里叶变换上,与时域矩形窗支撑区长度(时宽)不同,该频域矩形窗支撑区用带宽来衡量,其有效长度会大大增加。当频域窗W(f )为矩形窗时,对照式(8)并根据对偶原理,可知脉压的时域输出为:

其中,IFFT为逆傅里叶变换。
FFT与IFFT在形式上是一致的,辛格函数的主瓣宽度取决于窗函数的有效支撑宽度,宽度越大,分辨率越好。受多种因素(如近端盲区,多普勒模糊等)限制,脉冲体制的发射信号时宽不可能太大,而通过频率调制,窗函数的有效支撑宽度拓展到频域后会成几何递增。在相同脉冲宽度条件下,LFM和NLFM信号带宽相比传统简单波形会大大提高,故距离分辨率更优。而进一步,在相同带宽的条件下,LFM比NLFM脉压后的主瓣宽度会窄,这是前者的频域窗有效支撑宽度相对较大造成的。
由式(9)知,频域矩形窗反变换到时域同样为辛格函数。进一步,当W (f )不为矩形窗时,如海明窗,等效于对矩形窗作了加权处理,此时频域窗类似于“钟形”,由于NLFM脉压时频域窗的有效支撑宽度变小,反变换到时域后会使旁瓣降低,同时主瓣会有所展宽。而根据能量守恒定律,主瓣展宽后能量主要集中到主瓣区域,相应地旁瓣能量则会显著降低。但NLFM波形脉压后的窄主瓣和低旁瓣设计是互为矛盾的,在信号设计和实际应用时要根据需求折中考虑。
3 仿真实验
为验证各种窗函数设计的NLFM的脉压性能及其一般规律,下面用以3.1节给出的窗函数进行仿真。仿真参数为:脉冲宽度t=20us,信号带宽B=10MHz,采样频率fs=20MHz,高斯窗中的常数K=23.5。
3.1 窗函数及时频曲线
图1为四种窗函数的比较图,各窗对应的有效支撑区间长度由矩形窗到高斯窗逐渐减小。由3.2节的脉压分析,可初步推理出脉压后的主瓣宽度会逐渐增大。计算各窗函数的群延时函数到时频函数的变换,涉及到反函数求解,很难写出显示表达式,需要用到数值计算,本文采用样条插值方法进行时间等间隔重采样,通过插值可以反求出等间隔时间对应的频率值。需注意的是,该方法只在频率和时间一对一对应的条件下才适合,目前所设计的NLFM都满足该条件。

图1 四种窗函数
3.2 脉压输出及性能分析
根据各窗函数的时频曲线得到相应NLFM信号。图2给出了所设计信号的脉压输出,其中矩形窗对应的LFM调频信号的脉压结果,显然NLFM信号具有更低的旁瓣。图3(a)和图3(b)分别为脉压输出的主瓣局部放大和旁瓣局部放大图,不难看出:尽管NLFM具有较低的旁瓣,但是以主瓣展宽为代价的。表1定量比较了脉压后信号的-4dB主瓣宽度和峰值旁瓣比(第一旁瓣与主瓣峰值比)。由图3和表1可看出,设计的四种发射信号随着窗函数有效支撑区间的减小,其主瓣宽度呈递增趋势,而第一旁瓣幅度呈递减趋势,这与3.2节的分析是相吻合的。
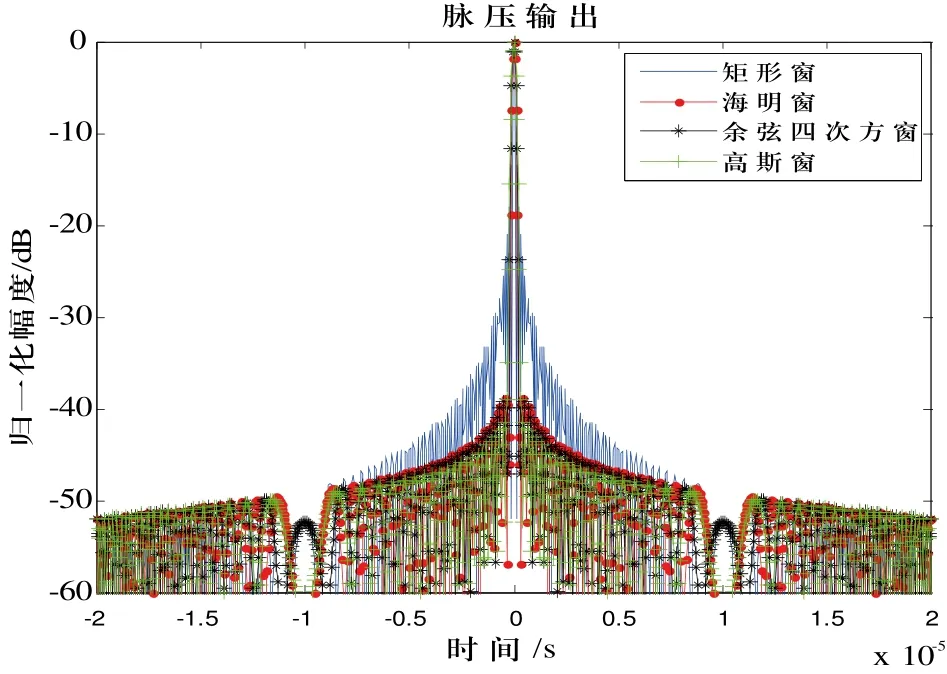
图2 脉压输出
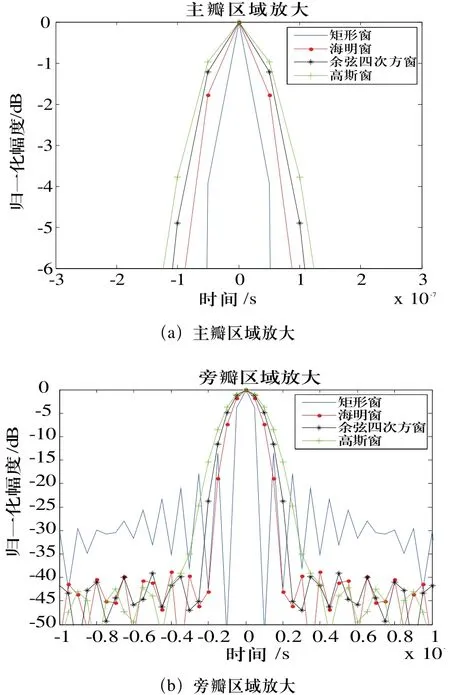
图3 局部放大结果

表1 脉压结果对比分析
4 结束语
本文从矩形窗函数的(逆)傅里叶变换视角入手,分析了NLFM的设计及脉压性能。分析指出,
相对传统简单波形的时域窗,LFM和NLFM的频域窗函数有效支撑区长度的增加(即带宽增大)是获得距离高分辨的关键,这与现有分辨率理论是一致的,随着支撑区长度的缩小,NLFM波形主瓣展宽。但是有效支撑区仅反映了NLFM设计中一个因素,若要得到性能优越的NLFM波形,必须对群延时函数施加更多的限制,如平滑性,曲率等,这将是下一步研究的方向。
[1] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1984.
[2] T. Collins and P. Atkins. Nonlinear frequency modulation chirps for active sonar[J]. IEE Proceedings, Part F,1999,146(6): 312-316.
[3] 张良. 一种NLFM脉压波形的优化设计方法[J]. 现代雷达, 1994, 16(5): 27-34.
[4] 武建辉. 多波形频域数字脉冲压缩系统的研究[D]. 电子科技大学, 2001.
[5] 黄勇, 彭应宁, 张瓅玶, 等. 基于调频函数和遗传算法的非线性调频信号产生方法[J]. 电子学报, 1999, 27(11):77-79.
[6] 何学辉, 陶海红, 吴兆平, 吴顺君. 一种改进的非线性调频信号设计[J]. 电子学报, 2009 37(8): 1784-1788.
[7] 苏扬. 大时宽带宽积信号的波形选择研究[J]. 武汉理工大学学报, 2004, 26(3): 15-17.

