一种保角参数化的面积变形的优化方法

胡建平，谢 琪，左 平

(1.东北电力大学理学院，吉林 吉林132012;2.空军航空大学 基础部，长春130022)

曲面参数化是纹理映射、重新网格化、网格变形、网格压缩、曲面拟合等许多数字几何处理算法的基本工具［1］。在这些应用背景下，源于表示形式的简单、灵活以及受各种图形硬件广泛支持的优点，曲面通常被表示为三角网格，它的参数化也就是通常所说的三角网格的参数化。三角网格的参数化的目标是寻求一个三角网格曲面与同它拓扑等价的简单区域(如平面、球面等)的一一映射，通过参数化映射所得的简单区域上的网格称为参数网格。从数学角度来看，这样的一一映射是很多的，寻找它并不是一件很难的事情，问题在于如何在这么多映射中找到一个相对比较“好”的映射?人们通常使用曲面的一些诸如角度、面积、长度等几何内在的属性的变形程度来衡量三角网格参数化的好坏［2］。

由于任意复杂的模型都可以切割成很多同胚于圆盘的区域，将它们分别参数化到平面上即可完成对整个模型的参数化。因此，三角网格平面参数化是网格参数化迄今为止研究得最多的话题。曲面参数化早期被引入到计算机图形学的应用—纹理映射也是以平面参数化为基础的。对于任何同胚于圆盘的可定向的光滑的二维流形曲面来说，黎曼映射定理保证了保角的平面参数化总是存在的。但是对于三角网格来说，黎曼映射定理并不一定成立。在实际计算中，通常是最小化与网格角度变形相关的度量来得到保角参数化。现有的保角参数化方法按照最小化与网格角度变形相关的度量的种类可以分为固定凸边界的方法、基于圆模式的方法以及基于角度展平的方法等［3］。由于保角参数化在能量最小化时没有考虑到原始网格曲面的面积属性，因此对于具有复杂结构的三角网格通常会产生比较大的面积变形，一定程度上影响了其在纹理映射、重新网格化等数字几何处理的应用。

针对此类问题，本文提出了一种优化方法，该方法通过引入保角参数网格顶点的平均值坐标权和面积变形因子对保角参数化进行优化。通过典型的三角网格模型的实验比较可以看出，本文方法所得的参数化的面积变形较保角参数化有明显改善，同时角度变形接近于保角参数化。

1 优化方法

三角网格模型M可以表示为一个二元组(V，K)，其中V表示网格中顶点的集合{vi∈R3}，K是一个单纯复型，包含M中所有拓扑连接关系的集合。K里面的元素有三种类型:顶点{i}，边{i，j}和面{i，j，k}。我们记K中边的集合为E，面的集合为F。如果{i，j}∈E，则称顶点{i}和顶点{j}是邻居。顶点{i}的1 环邻居被定义为 N(i)={j|{i，j}∈ E}，它的星形邻域被定义为 Star(i)= ∪i∈s，s∈Ks。如果顶点{i}的星形邻域在网格中对应的区域同胚于圆盘(半圆盘)，则该点称为内部顶点(边界顶点)。

设M在平面区域的保角参数网格为P，可以通过固定凸边界的方法［4］、基于圆模式的方法［5］等得到(图1)。本文提出的优化方法是将保角参数网格P的边界顶点固定，然后通过求解一个线性方程组得到内部顶点在平面上的对应顶点ui。该线性方程组是通过保角参数网格顶点的平均值坐标权和面积变形因子得到。它的具体形式如下:

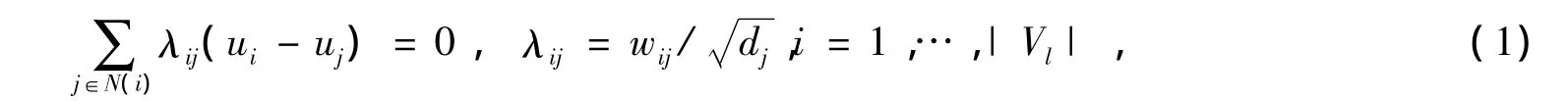
式中uj表示顶点vi的一环邻点vj在平面上对应的顶点，wij和dj分别表示顶点在保角参数网格P中对应顶点pj的平均值坐标权和面积变形因子，|Vl|表示三角网格中的内部顶点的数目。

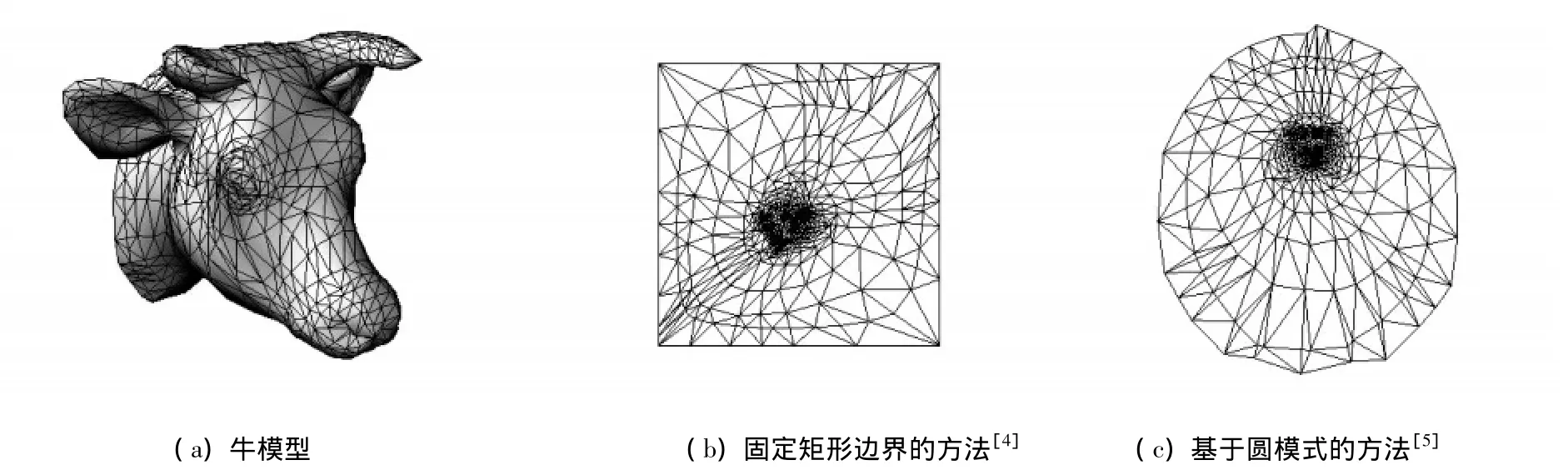
图1 通过不同的方法得到的保角参数化网格

平均值坐标权是通过调和映射满足平均值定理得出来的［4］。由于调和映射是通过最小化离散的Dirichlet能量得到的，因此平均值坐标权可以减少参数化的角度变形。它的计算公式如下:

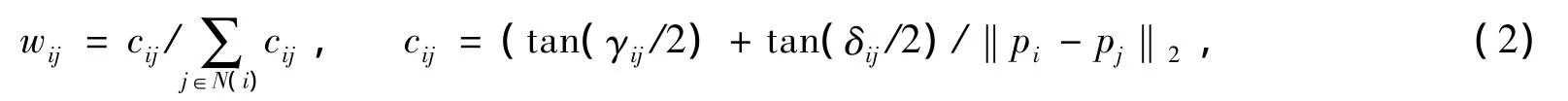
其中pi，pj分别表示保角参数网格P的一条边的两个顶点，γij，δij表示该边与相邻顶点形成的角度(图2)。

保角参数网格顶点的面积变形因子可通过三角形的面积变形进行计算。对于保角参数网格的一个三角形U，它的面积变形定义为它在原始网格中所对应三角形T同它的面积之比，即:

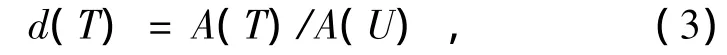
式中A(·)表示三角形的面积。则每个顶点pi的面积变形di就可定义为它在原始网格中对应顶点vi的一环相邻三角形Tj的面积变形的加权平均，即为:

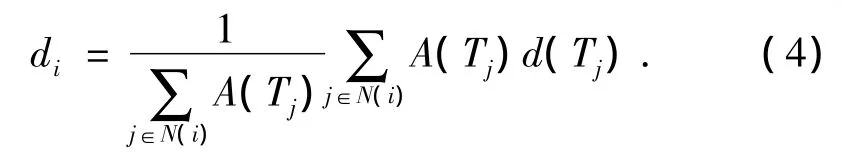
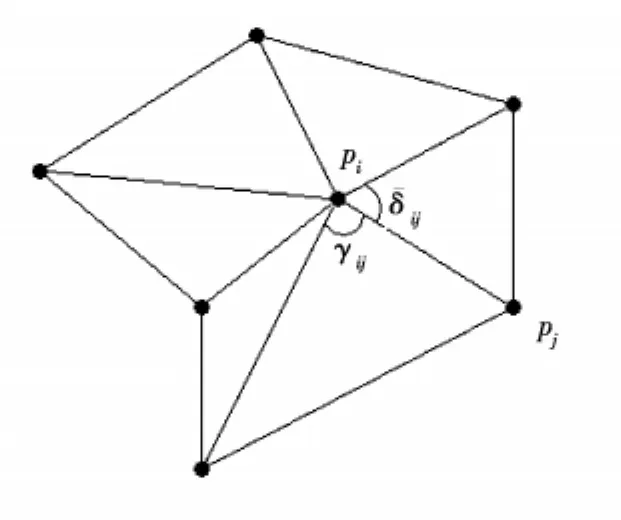
图2 平均值坐标权的计算

这种优化方法的本质是通过引入平均值坐标权控制优化参数化角度变形，同时对面积变形比较大的顶点对平均值坐标权进行缩放，即采用较小的权值，使得该顶点朝面积变形较小的区域移动，从而减少保角参数化的面积变形。优化时以顶点的面积变形的平方根进行缩放，控制了面积变形比较大的顶点移动的距离，使得优化后的参数化的角度变形不至于发生太大的变化。

2 实验结果分析和讨论

通过将原始网格的法向量映射到参数区域，或者将参数区域上棋盘等纹理映射到原始网格上的视觉效果是衡量参数化变形的一个直观标准;除此之外，还可以通过参数网格与原始网格之间的面积相对误差和角度相对误差等测度来衡量参数化的面积和角度变形程度，它们的计算公式如下:

其中|F|表示原始网格M的三角形数目，A(Ti)表示网格M的第i个三角形Ti的面积，A()表示参数网格中与Ti所对应的三角形的面积，θij表示网格M中三角形Ti的第j个角度表示参数网格中θij与对应的角度。

为了检验本文优化方法的有效性，我们选用了几种典型的三角网格模型如猫、手、人头、牛头模型(手和牛头模型具有细长的结构)进行测试，通过固定矩形边界的方法［4］和基于圆模式的方法［5］所得的保角参数化作为初始输入进行优化，给出了原始网格的法向量映射到优化前后的参数网格的效果图，以及优化前后参数化的角度和面积变形统计，如图3、图4、表1所示。通过这些比较可以看出，本文方法所得的参数化的角度变形接近于初始输入的保角参数化，但是面积变形明显减少。

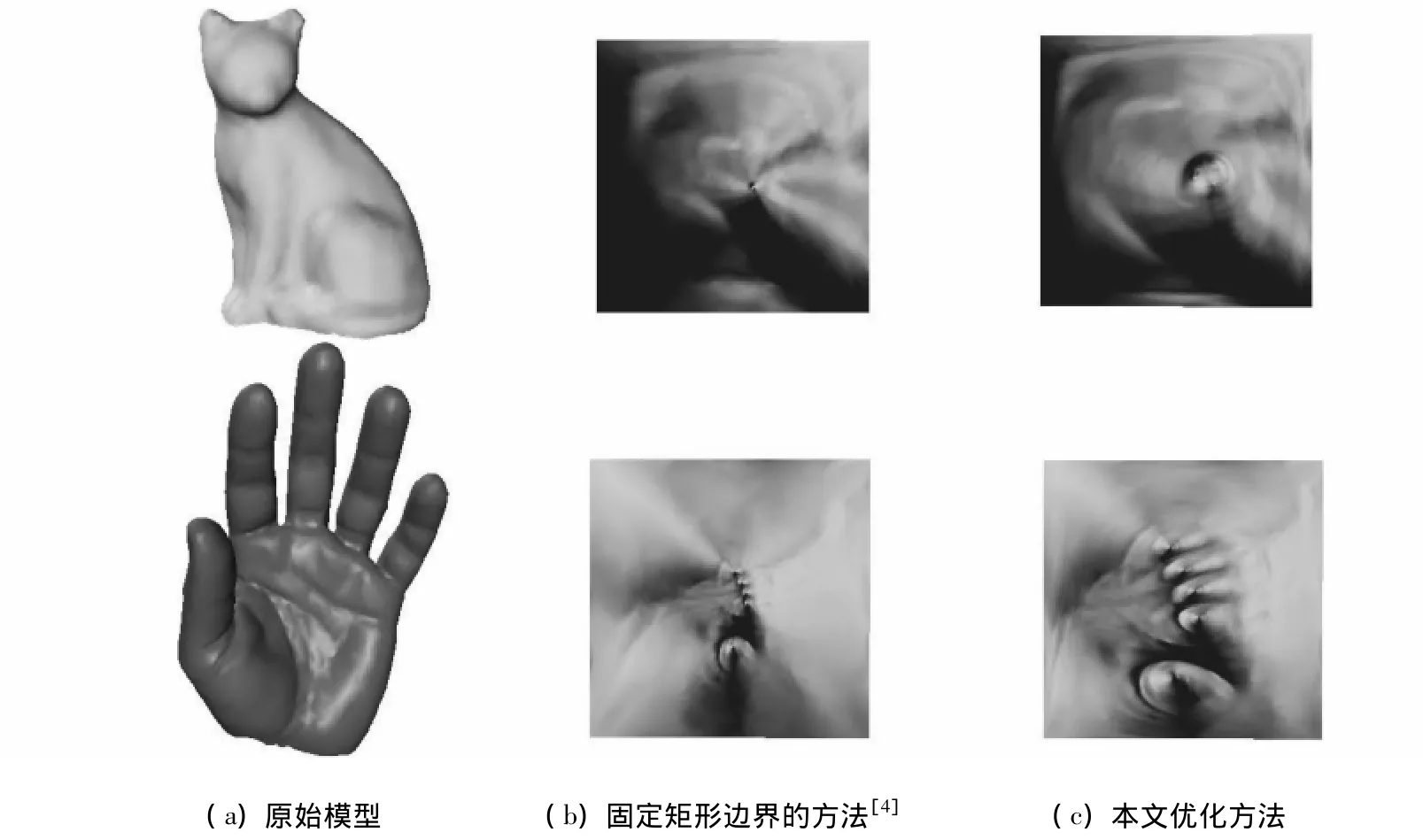
图3 参数化结果比较

表1 一些典型模型参数化变形统计比较

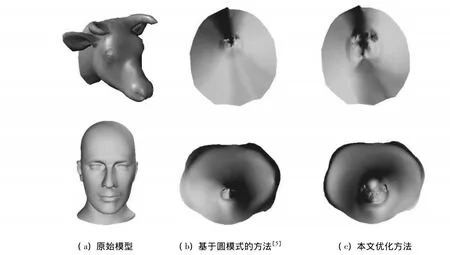
图4 参数化结果比较

3 结论和未来工作

本文通过引入保角参数网格的平均值坐标权和顶点的面积变形因子对保角参数化进行优化，明显减少了复杂结构物体的保角参数化的面积变形，在纹理映射、重新网格化、网格变形等数字几何处理的应用中具有重要的价值。在未来的研究中，我们打算将本文的参数化方法应用在纹理映射、重新网格化、网格变形等数字几何处理的应用中。

［1］Sheffer，A.，Praun，E.，Rose K.Mesh Parameterization Methods and their Applications［J］.Computer Graphics and Vision，2006，2(2):105-171.

［2］彭群生，胡国飞.三角网格的参数化［J］.计算机辅助设计与图形学学报，2004，16(6):731-739.

［3］胡建平.数字几何处理中球面参数化和重新网格化研究［D］.辽宁:大连理工大学，2009.

［4］Floater，M.S.Mean value coordinates［J］.Computer Aided Geometric Design.2003，20(1):19-27.

［5］Kharevych，L.，Springborn，B.，Schr?der，P.Discrete conformal mappings via circle patterns［J］.ACM Transactions on Graphics.2006，25(2):412-438.