对人工合成金刚石的三阶非线性光学极化率的研究
赵建勋 蒋大勇 高 尚 梁庆成 秦杰明
(长春理工大学材料科学与工程学院 吉林 长春 130022)
0 引言
金刚石是一种宽禁带半导体材料,其禁带宽度为5.5eV[1]。人们研究发现金刚石具有很多优秀的光学和电学性质,如高击穿电场(~107V/cm)、高载流子迁移率(~0.2m2(V·s ))、高热导率(~20W(cm·K))[2]、高电阻率(~1016Ω·cm )和低的介电常数(5.66)[3]。 金刚石对从 225nm 到远红外波段的光有很好的透明性。
金刚石属于m3m点群,具有反演对称中心。根据电偶极矩近似理论,金刚石不能产生二阶非线性光学效应,三阶非线性光学效应是金刚石最主要的非线性光学效应。为了利用金刚石的三阶非线性光学效应,其三阶非线性光学极化率的测量是必需的,然而很少见到相关的报道。Anastassakis等在Ⅱ型金刚石中观察到了克尔效应[4],他们把双折射晶体放在两个正交的偏振片之间,测量由克尔效应产生的相位差,得到克尔系数,然而这种方法的误差很大。Arva通过紧束缚轨道模型计算了三阶非线性光学极化率[5]。Levenson采用混频法研究了合成金刚石和天然金刚石的三阶非线性光学极化率色散性质[6],该方法使用的设备复杂且昂贵。
我们基于克尔效应理论和横向电光调制系统,测量了人工合成的Ⅰ型金刚石的三阶非线性光学极化率张量的元素。该方法所需设备简单,测量过程简单,同时具有较高的测量精度。
金刚石属于立方晶系,其折射率是各向同性的。没有外加电场时,金刚石的折射率椭球是球型;如果在金刚石上外加电场,其对称性将降低,并变为双折射晶体。折射率的变化量正比于外加电场强度的平方。当外加电场沿着金刚石晶体的[111]晶向,金刚石成为了单轴晶体,[111]晶向是其光轴。
1 实验方案

图1 实验中使用的金刚石外形图
理想的金刚石晶体外形为立方八面体,如图1(a)所示。实验中使用的金刚石样品为郑州中南杰特有限公司提供。如图1(b)所示,样品是不规则的立方八面体外形,包括八个六边形晶面和六个四边形晶面。六边形晶面为{111}面,四边形晶面为{100}面。相对的六边形(四边形)晶面互相平行。纯净的金刚石晶体是透明无色的,在实验中,使用的是非故意掺杂的Ⅰ型金刚石。因为样品内含有一定量的氮,所以样品呈现黄色。尽管样品不是纯净的,样品的电阻率仍然很好(~108Ω·cm),室温下载流子浓度只有3×107cm-3。因此载流子效应可以忽略。
当调制电场E=E0cos(ωt)沿着[111]晶向作用在金刚石样品上,根据克尔效应的理论,沿着光轴([111]晶向),取[111]晶向为直角坐标系中的z轴,可由下式表示,

式中Sij是克尔系数,n0是无外加电场时金刚石的折射率,E0是外加电场强度。根据克尔系数与三阶非线性光学极化率张量之间的关系,式(1)可写为

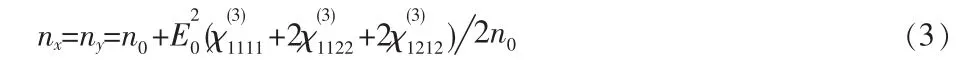
当光垂直于外加电场是,可以获得最大的相位延迟

式中L是在外加电场作用下样品中的光程,λ是探测光在真空中的波长。由于金刚石是硬度最高的材料,将金刚石处理成所需要的外形是很困难的。因此基于金刚石样品的外形,我们选择[111¯]轴为探测光的传播方向,[111¯ ]轴与光轴的夹角为 θ=70.53°,于是在(111¯)面内的 o 光和e光的折射率分别为
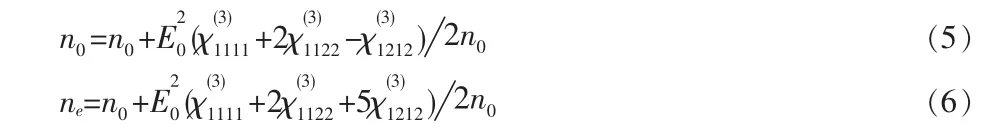
所以,o光和e光的相位差为

2 实验过程
样品被固定在两个钢质电极之间,为了避免在电极与样品之间有空气隙,把软金属铟夹在了电极和样品中间。电极和相对的(111)面接触,为了避免放电,使用绝缘胶将电极包裹好。电极与样品的接触面略小于样品表面。把样品和电极安装在一个中心有孔的绝缘板上,探测光将可通过该孔和样品。实验中的电极结构(如图2所示)。在实验中,需要在样品上外加很高的交流电压,因此低频信号发生器的输出送入音频功率放大器中,用来产生更高功率的信号,这一个高功率的信号再通过变压器转变为需要的交流电压。
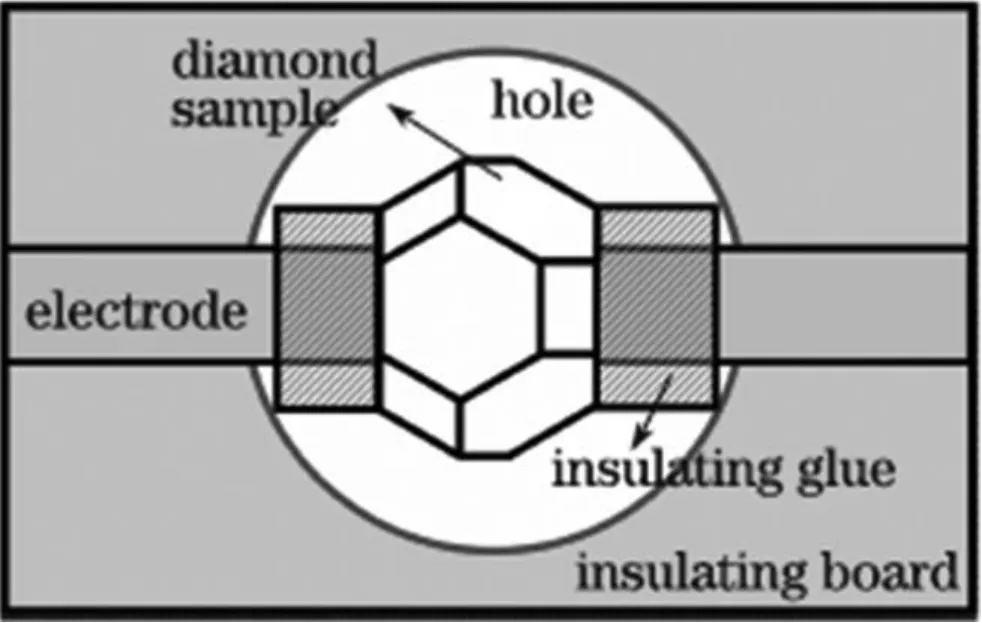
图2 电极结构的俯视图

图3 实验中使用的横向电光调制系统装置图
实验中我们搭建了一个横向电光调制系统,如图3所示,采用波长为650nm的连续波激光二极管作为光源,以硅光电探测器接收探测光束。[111¯]轴设置在水平方向。取空间竖直方向为y′轴,起偏器的偏振方向与y′轴成45°,检偏器的偏振方向与起偏器的偏振方向互相垂直,四分之一波片的快轴平行于y′轴,透镜1把光束聚焦到样品上,从样品射出的光经过透镜2转变为平行光。透镜1和透镜2都为长焦距透镜,因而样品内的光束仍然可以被看做是平行光。从检偏器输出光束的光强经琼斯矩阵计算为

式中Iin是入射光的光强,Δø是式(7)表示的相位差。通常Δø远小于1,因此式(8)可表示为

设调制电压为V=V0cosωt,将该调制电压加载在样品上,d是电极之间的距离,所以外加电场强度可表示为E0=Vd=V0(cosωt)d,这样式(9)可变为

从式(10)可以看出,输出光束包括了直流成分和交流成分,其中直流成分不可被锁相放大器探测到,交流成分可以被锁相放大器探测到。当没有调制电压加在样品上时,输出光强为I1=Iin2,斩波扇以284Hz将探测光束变为不连续的光束,硅光电探测器与锁相放大器相连,测得的光电信号为U1=MI1=MIin2=45.9mV,式中M为光学元件和锁相放大器、光电探测器的响应度有关的因子。被光电探测器接收的光信号是方波,它可以被表示成傅里叶级数形式,然而锁相放大器只能探测基频的正弦信号,因此应考虑引入修正因子2π[7],

然后,移去斩波扇,把频率为142Hz的调制电压加在样品上。锁相放大器的参考信号平率设定在调制电压的两倍,这样就可以探测到交流信号(2ω),探测到光电信号U2可以表示为
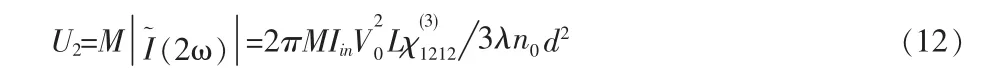
从式(11)和式(12)可以得到 U2U1的表达式为

U2U1与V0之间的关系可以通过改变调制电压的幅度来测量,如图4所示。测量结果表明,两者之间是很好的二次函数关系。从拟合函数得到二次项系数为

使用游标卡尺测得电极之间的距离为1.95mm,样品中的光程为1.41mm,金刚石在650nm处的折射率为2.4105,因此根据式(14),可计算得三阶非线性光学极化率张量的元素=2.17×10-22m2V2,根据克尔系数与三阶非线性光学极化率元素之间的关系,可得克尔系数S44=S1212=1.93×10-23m2V2。
实验中不需要测量探测光的绝对光强,而且横向电光调制系统达到了最大的灵敏度和线性度,相位延迟也达到了现有样品外形条件下的最大值,以上这些保证了测量的精度。
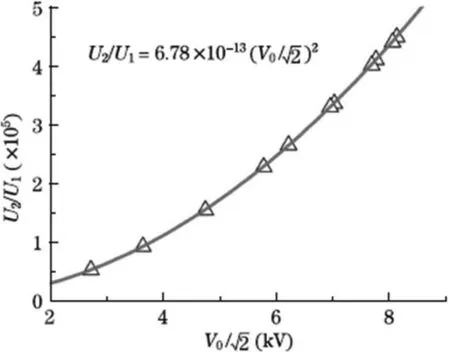
图4 U2U1与V0之间的关系
3 结论
我们提出了一种测量宽禁带半导体的三阶非线性光学极化率张量的办法,该方法简便易行,且无需测量绝对光强。通过实验测得了人工合成的金刚石单晶的三阶非线性光学极化率张量的一个非零元素。
[1]S.Almaviva,M.Marinelli,E.Milani,G.Prestopino,A.Tucciarone,C.Verona,G.Verona-Rinati,M.Angelone,M.Pillon,Extreme UV single crystal diamond Schottky photodiode in planar and transverse configuration,Diamond[J].Relat.Mater.2009,18:101-105.
[2]Z.C.Dong,A.S.Trifonov,N.V.Suetin,and P.V.Minakov,Electroluminescence of diamond films induced by a scanning tunneling microscope[J].Surface Science,2004,549:203-206.
[3]M.I.Eremets,Refractive index of diamond under pressure,Semicond[J].Sci.Technol.1991,6:439-442.
[4]E.Anastassakis and E.Burstein,second-order electro-optic effect in diamond,J.Opt[J].Soc.Am.1971,61:1618-1622.
[5]K.Arya,S.S.Jha,Dispersion in the anisotropy of optical third-harmonic generation in silicon,Phys[J].Rev.B 1979,20:1611-1618.
[6]M.D.Levenson,N.Bloembergen,Dispersion of the nonlinear optical susceptibility tensor in centrosymmetric media,Phys[J].Rev.B:1974,4447-4463.
[7]K.Cao,Z.Chen,C.Ren,G.Jia,T.Zhang,X.Liu,B.Shi,J.Zhao,Measurement of secondorder nonlinear optical susceptibility of cBN crystal synthesized at high pressure and high temperature[J].Microelectronics J.2009:40,70-73.

