带油耗的单车场开放式车辆路径问题研究

王明阳，陈 鑫， 张丽华 （沈阳师范大学，辽宁 沈阳110034）

车辆路径问题 （Vehicle Routing Problem,VRP）最早由Dantzing和Ramser[1]于1959年提出,之后产生了这一问题的许多变种，例如：多车型车辆路径问题 （Heterogeneous-vehicle Vehicle Routing Problem，HVRP）[2-4]；多车场车辆路径问题[5-6]；开放式车辆路径问题[7-11]等等。

针对各种车辆路径问题，大部分文献的目标函数大致由两部分组成： （1）车辆的启动费用； （2）车辆的行驶费用。首先，车行驶费用与行驶距离有关，而现实生活中，随着油价的不断上涨，在考虑车行驶费用的时候除了考虑行驶距离对于行驶费用的影响，耗油量对于行驶费用的影响也是很大的，所以熊浩[12]、唐加福[13]等人在目标函数中考虑了油耗成本对线路的影响，但是他们考虑的都是封闭式车辆路径问题。而由于各厂商现在大部分都采用物流外包，所以有必要考虑路径为开放形式的，这样更符合实际生活，故此本文考虑带油耗的开放式车辆路径问题，即：车辆在对其负责的路径上的客户进行服务时，不必回到原车场，而是终止于它所服务的最后一个客户点。另外，由于一个物流公司所服务的客户其需求不同，因此可能需要该物流公司派出不同类型的车辆对其进行服务，即使所服务的客户没有特殊要求，物流公司本身也可能具有不同型号的车辆，而不同车型的车辆其启动费和最大容量是不同的，由此会对物流公司的车辆分配方案产生影响，所以本文研究的车辆路径问题还要考虑车辆的启动费用及容量。

1 问题描述

本文研究一种带油耗的单车场多车型开发式车辆路径问题。它可以描述为：有一个车场，车场中共有L种类型的车辆。设第l 1≤l≤（）L 种类型车共有Kl辆 （Kl足够大，即各种类型的车足够用），每辆的容量为Ql，启动费用为Cl。设车场共有K辆车，那么该车场共为N个客户点服务，其中第i（ 1≤i≤N ）个客户点所需货物

重为gi。配送车辆从车场装上货物出发，为N个客户送货，要求每个客户只由一辆车为其完成送货任务，车辆将货物运送完毕后结束于其最后服务的客户点。被派出完成配送任务的每辆车的费用都为它所产生的油耗与它的启动费用，目标为使所有被派出的车辆的费用之和最小。

2 数学建模

用0表示车场，cl表示第l（ 1≤l≤L ）种类型车辆单位距离单位重量的燃油费用，表示第l（ 1≤l≤L ）种类型的第k（ 1≤ k≤Kl）辆车从节点i（ i∈ ｛0,1,…,N ｝）驶向节点j（ j∈ ｛1,…,N ｝）时其上的载重量，dij（i,j=0,1,…,N ）表示节点i与节点j之间的距离， 其中dii=0（ i=0,1,…,N ）。与都是0-1决策变量，当第l（ 1≤l≤L ）种类型的第k（1≤ k≤Kl）辆车从节点 i（ i∈ ｛0,1,…,N ｝）驶向节点j（ j∈｛1,…,N ｝）（i≠j）时xlikj=1， 否则当节点 （客户）i（i∈ ｛1,…,N｝）由第l（ 1≤l≤L ）种类型的第k（ 1≤ k≤Kl）辆车服务时否则于是上述问题可用下列0-1整数规划模型进行描述：

其中： （1）的第一项与第二项分别表示所有配送车辆总的油耗和总的启动费用； （2）表示所用的每类型车车数不超过此类型车数； （3）表示每个客户点恰好被访问一次； （4）表示离开每个客户点的车辆数小于或等于进入该客户点的车辆数； （5）表示被派遣的每一辆车的载重量都不超过其容量。

3 模型求解

因为开放式车辆路径问题 （OVRP）是NP难的[8]，而本文讨论的问题是对OVRP的扩展，所以本文的问题也是NP难的，因此下面采用禁忌搜索算法对其进行求解。

3.1 禁忌算法中的初始解的求法

由于禁忌搜索算法求解的好坏在一定程度上依赖于其初始解，所以下面用改进的最近邻算法求初始解，以得到更优的结果。

改进的最近邻算法：M：表示未安排路线的客户集合；s：用以累加一条路径上客户点的需求量；r：存储一条未完成路径其车辆的容量与其当前最后一个节点处需求量的累加值（）s之差；M'：存储本文讨论问题中一个解的全部路径；lujing：存储当前要生成的路径，如果生成完毕，将其加入到M'中；j：存储当前未完成路径中的最后一个节点；i：存储当前M中被选中要为其安排路线的那个点。

第一步：初始化。令M←1,…,｛｝N ， s←0， M'←Ø， lujing←Ø。第二步：当M≠Ø时，重复以下步骤，否则，算法结束，输出M'。步骤1：如果lujing=Ø。随机选一车型，记为k，将其添加到lujing中，即在M中选择其需求量与它和车场距离之比最大者， 将其序号赋给i， 令r-gi，如果lujing≠Ø，在M中选取其需求量与它到lujing中最后一个节点j的距离比值最大者，将其序号赋给i，

本文的问题要求油耗尽量小，为了实现这一目标，在改进的最近邻算法中生成一条新的路径时，在未安排路线的节点中选取其需求量与它到当前未完成路径的最后一个节点 （如果当前未完成路径为空时，其最后一个节点为车场）的距离之比最大或次大者进行添加，这样很明显可以降低油耗。

3.2 禁忌算法中解的表示

由于上述问题为多车型单车场问题，本文用MATLAB实现该禁忌搜索算法，为了便于进行邻域操作，所以采用车型代替车场，用一维元胞数组来表示问题的一个解，例如，设一车场共有3种类型的车辆，该车场为10个客户完成送货任务，则可以用1，2，3表示三种车型，1～10表示10个客户，则一维元胞数组：

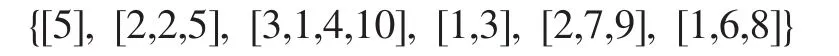
表示问题的一个解其含义如下，此解共有5条路径：第一条路径：第2种类型的一辆车从车场出发到达客户2，再由客户2出发到达客户5结束；第二条路径：第3种类型的一辆车从车场出发到达客户1，再由客户1出发到达客户4，再由客户4出发到达客户10结束；第三条路径：第1种类型的一辆车从车场出发到达客户3结束；第四条路径：第2种类型的一辆车从车场出发到达客户7，再由客户7出发到达客户9结束；第五条路径：第1种类型的一辆车从车场出发到达客户6，再由客户6出发到达客户8结束。

3.3 禁忌算法中邻域操作

由于本文问题中车辆具有不同的类型，加上要减少车辆的启动费用，所以下面采用一些特殊的邻域操作来减少所使用车辆的剩余容量以及减少所使用的车辆的数目。

随机从M'（其含义同改进的最近邻算法中的M'）中取两条路径，再分别从两条路径中取出两个节点：

（1）如果两节点均为车型，则分别将取出的两路径的车型更换成容量与其路径装载量 （该路径上所有客户点需求量之和，以下同）最近的车型。

（2）如果两节点一点为车型，一点为客户点，将客户点插在另一路径的车型之后，并在原路径中将其清除，如果清除客户点之后此路径中还有客户，就将此两条路径的车型更换成容量与其装载量最近的车型。如果清除客户点之后这条路径已经没有客户，则将其在M'中删除，只将另一条路径的车型更换成容量与其装载量最近的车型。

（3）两节点均为客户点，将第二个客户点插在第一个客户点之后，并在原路径中将其清除，如果清除客户点之后此路径中还有客户，就将此两条路径的车型更换成容量与其装载量最近的车型。如果清除客户点之后这条路径已经没有客户，则将其在M'中删除，只将另一条路径的车型更换成容量与其装载量最近的车型。

3.4 禁忌算法中评价值的计算

为了扩大搜索范围，本禁忌搜索算法允许各次迭代中由不可行解产生邻居，但为了在算法结束后能够得到问题的可行解，因此对不可行解进行惩罚，设p为惩罚因子，且令若解x中共有ux条路不可行，而设x对应的目标函数值为fx，那么解x的评价值为

3.5 禁忌搜索算法中禁忌对象、禁忌长度

本文所选的禁忌对象及禁忌长度参照文献[14]。

4 例 子

假设某一车场为30个客户配送货物，该车场共有3种类型配送车辆，每种类型车辆足够用，第1，2，3种车型每辆车的容量分别为10，20，50，启动费用依次为100，150，300，车场坐标为 （11,11），各个客户的需求量及坐标如下列表1～2所示。要求车场合理为各客户配送货物并使配送费用 （总油耗加上总启动费用）最少。

调用算法1后得到的初始可行解为：

表1 各个客户的需求量

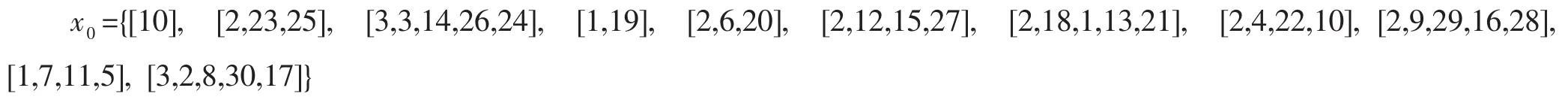
x0对应的目标函数值 （总的费用）为2.6553e+004；

运行完禁忌搜索算法后产生的可行解为：

x1对应的目标函数值 （总的费用）为：2.1686e+004。

对此例而言，禁忌搜索算法对初始解的改善是很明显的。

5 结 论

本文针对带油耗的单车场多车型车辆路径问题采用禁忌搜索算法进行求解，提出了改进的最近邻法求初始解，此算法可以降低油耗，在禁忌搜索算法中为了减少所派遣车辆的剩余容量和所派遣的车辆数而采用了一些特殊的邻域操作，算例表明该算法易于实现，且效果较好。本文为单车场问题，而对于多车场问题我们将进行下一步研究。

[1] Dantzig G..B.,Ramser J.H.The truck dispatching problem[J].Management Science,1959,6(1):80-91.

[2] 杨文霞，郭海湘，杨娟,等.改进的扫描法求解单车场多车型车辆路径问题[J].物流技术，2010,4(215):50-53.

[3] 贾立双，李静.基于一种改进算法的单车场多车型车辆调度研究[J].中国制造业信息化，2008,37(19):8-10.

[4] 洪波，郎茂样.多车型配送车辆调度问题的模型及其禁忌搜索算法研究[J].长沙交通学院学报，2005(3):73-77.

[5] 钟石泉，贺国光.多车场车辆调度智能优化研究[J].华东交通大学学报，2004(6):25-29.

[6] Oberlin P.,Rathinam S.,Darbha S.A Transformation for a Multiple Depot,Multiple Traveling Salesman Problem[C].American Control Conference,2009:2636-2641.

[7] Sariklis D,Powell S.A heuristic method for the open vehicle routing problem[J].Journal of the Operational Research Society,2000,51:564-573.

[8] 符卓.开放式车辆路径问题及其应用研究[D].长沙：中南大学 （博士学位论文），2003.

[9] 段风华，符卓.有软时窗多车场开放式车辆路径及其禁忌搜索[J].计算机工程与应用，2008,44(36):42-44.

[10] 钟石泉，杜纲，贺国光.有时间窗的开放式车辆路径问题及其遗传算法[J].计算机工程与应用，2006,34:201-204.

[11] 孙国华.带软时间窗的开放式满载车辆路径问题研究[J].船计算机工程与应用，2011,47(17):13-17.

[12] 熊浩.多车型车辆共享的MDVRP问题及其遗传算法[J].华中师范大学学报，2010,44(1):29-32.

[13] Tang J.F.,Zhang J.,Pang Z.D.A scatter search algorithm for solving vehicle routing problem with loading cost[J].Expert Systems with Applications,2010,37(6):4073-4083.

[14] 冯芳媛，张丽华，李阿慧.B2C电子商务中带退货的多配送站点车辆路径优化问题研究[J].物流科技，2011(7):15-19.