梯形波相电流驱动六相感应电机建模与控制

艾永乐， 王玉梅， KAMPER Marrten

(1.河南理工大学电气工程与自动化学院河南焦作454000;2.Department of Electrical＆ Electronic，Stellenbosch University，Stellenbosch 760000，South Africa)

0 引言

在众多类型的电机中，感应电机一直受到人们的青睐［1］。工业上使用的驱动器至少90%是采用感应电机驱动。感应电机的结构简单，坚固，制造成本低，维护容易，寿命长等优点已正在替代直流电机。由于电力电子器件额定电压和额定电流的限制和大功率驱动以及高可靠性的需求使得多相感应电机应运而生，以实现低压功率器件驱动大功率电机。

由文献［2－13］可知，为了获得更好的输出驱动性能，六相电机一般都采用矢量控制，但其缺点是需要复杂的派克变换和派克逆变换。因此本文提出一种新颖的控制策略，即梯形波相电流驱动下的六相感应电机气隙磁链直接转矩控制。本文主要采用有限元分析软件对六相感应电机每相电路建模，有限元分析计算结果进一步验证了理论分析结果［14］。最后通过所搭建的实验装置对六相电机的性能进行了实验验证。

1 六相感应电机有限元分析条件

梯形波相电流驱动下的六相感应电机直接转矩控制理论分析在文献［15－16］已给出了较详细的论述，这一部分主要是利用有限元分析软件对六相感应电机在自然坐标系进行数学建模。由于电机结构的对称性，仅需要分析电机截面图的一半区域即可。六相感应电机定子绕组布局图如图1所示，同时也注明了应用于有限元分析的部分。采用六相电机一半区域进行有限元分析，可以减少有限元个数，节省计算时间，同时又不致于影响整个问题的计算精确度。应用对称性，就可以得到整个电机的磁势分布。用于有限元分析六相电机横截面结构图和边界条件如图2所示。依据狄利克来边界条件，即将零磁势设置在定子磁轭外侧和转子轴上。

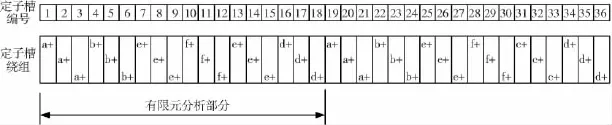
图1 定子绕组展开分布图Fig.1 Stator winding diagram and portion(18 slots)analysed

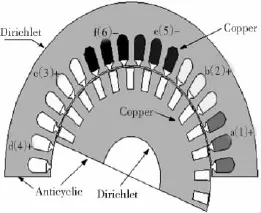
图2 六相电机横截面结构图Fig.2 Six-phase machine geometry and boundary condition

2 有限元分析

2.1 气隙磁通密度

由于气隙磁通的分布对电磁转矩的性能非常重要，所以首先研究仅有励磁电流作用下的气隙磁通密度的特性。

为了清晰可见，六相定子相电流［14］在0～t1作为励磁相的电流波形如图3所示。此时励磁电流IF取3.5 A。即在0～t1通入三相励磁电流 iaf，icf和 idf，而其余三相电流为零，在这种设置下，研究气隙磁通密度波形的质量。对应于t=0和t=t1/2时所通入励磁电流产生的气隙磁通密度波形如图4所示，即在t=0时励磁电流瞬时值为ic=id=－IF，而t=t1/2时三相励磁电流瞬时值为ia=－ic=IF/2，id=－IF，且幅值IF=3.5 A。这里可以清楚发现磁通密度波形图和励磁相电流同步变化，但平均幅值B随角位移变化很小，只在0.43～0.46 T之间有微小改变。

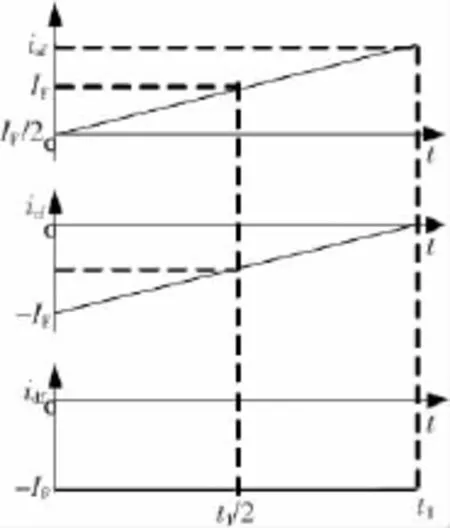
图3 在时间段0～t1三相电流的放大图Fig.3 Stator field current waveform during 0～t1

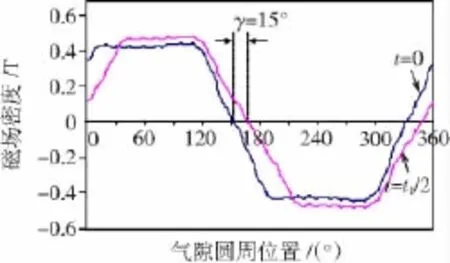
图4 不同时刻和相电流的平均气隙磁通Fig.4 Average air gap flux density at different times and phase currents

由图5可知，气隙磁通密度的幅值大小和幅值宽度会随着气隙磁通密度角位移的不同而变化;且磁通密度的脉动频率为12f1，这里f1是相电流的基波频率。脉动磁通密度会在每相转子绕组中产生纹波电压。从图5(b)可知幅值宽度在90°和104°之间改变。

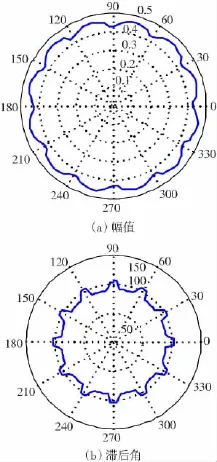
图5 气隙对角位的磁通密度幅值和滞后角Fig.5 Values of amplitude and plateau angle of flux density in the air gap versus angle position

2.2 稳态电磁转矩计算

六相感应电机稳态电磁转矩也可直接由有限元分析计算。斜槽电机的电磁转矩可由非斜槽子电机来计算，即

其中，Tn是应用麦克斯韦应力张量法所获得的第n个“非斜槽”子电机的电磁转矩。通过时步有限元分析，可计算出电机的电磁转矩。在磁动势平衡条件下，即2NsIT=7 NrIr，利用理论分析计算的定子转矩电流值IT和转子电流值Ir［15］，有限元分析计算出电磁转矩显示于第4部分的图13。由图13可知，电磁转矩和转矩电流几乎成线性关系，Te/IT的比值大约为2.91 N·m/A(12.81/4.4)。

2.3 电磁转矩脉动分析

众所周知，转子磁场速度和定子磁场的旋转速度是相等的。通过保持转子中7个特定相电流恒定，设置转子速度与定子励磁旋转速度相等，利用时步有限元分析法可以计算出脉动电磁转矩。在额定负载和磁动势平衡条件下，转差速度ωsl=150 r/min，IF=3.5 A，IT=2.2 A，Ir=5.6 A。额定负载下脉动电磁转矩如图6所示。转矩脉动低于7.6%(0.5、6.5)。由图6可知，电磁转矩的脉动频率为12f1。这和在2.1部分中分析的气隙磁通脉动频率一样。对图6进一步分析可以发现，该脉动转矩是由定子转矩相电流引起的。

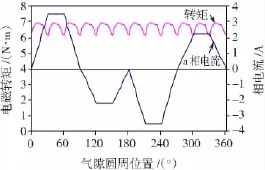
图6 额定条件下的转矩脉动Fig.6 Torque ripple at rated load condition

2.4 转子感应电压

为了研究六相感应电机转子第j相绕组开路电压的波形，即

其中，λj是第j个转子相绕组的磁链，仍采用时步有限元法来分析第j个转子相绕组开路电压。这种方法是定子磁场保持恒定，转子以150 r/min的速度旋转。定子侧通入相电流为ia=－ic=IF/2，id=－IF;ib=ie=if=0，由于定子相电流为常数，因此方程(2)可表示为

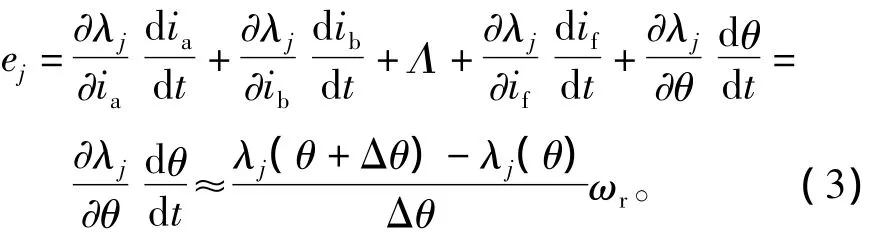
同样使用前向差分近似计算，在转子转速为150 r/min条件下，采用时步有限元分析计算得到的转子磁链和感应电压如图7所示。显而易见，其感应电压类似方波，和直流无刷电机的定子感应相电压相似。

图7 有限元分析计算转子感应电压Fig.7 FE calculated rotor induced voltage

3 定子相电路建模

在自然参考坐标系下，定子电压一般表示为

其中，vj，ij和 λj分别为第j个定子相电压、定子相电流和定子磁链。六相感应电机的定子相磁链是关于定子电流和转子电流的一个非线性函数，在理想的磁链平衡条件下，即定子转矩磁链被转子磁链抵消。此时，忽略定子转矩电流和转子相电流，定子磁链表示为

采用EpiData3.1软件建立数据库并进行数据录入。采用SPSS 22.0软件进行统计学分析。定量资料组间比较采用单因素方差分析，定性资料组间比较采用χ2 检验，以 P< 0.05为差异有统计学意义。

λS和iS都是列向量，即

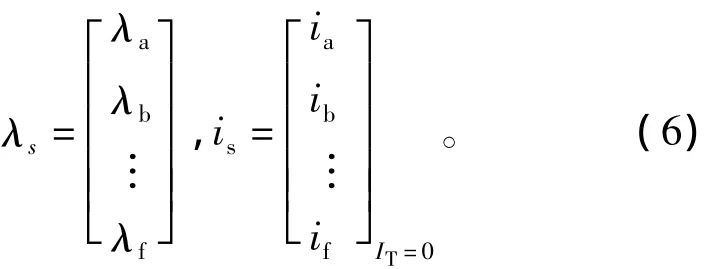
通过对定子磁链λs求偏导后表示为

为自感矩阵;

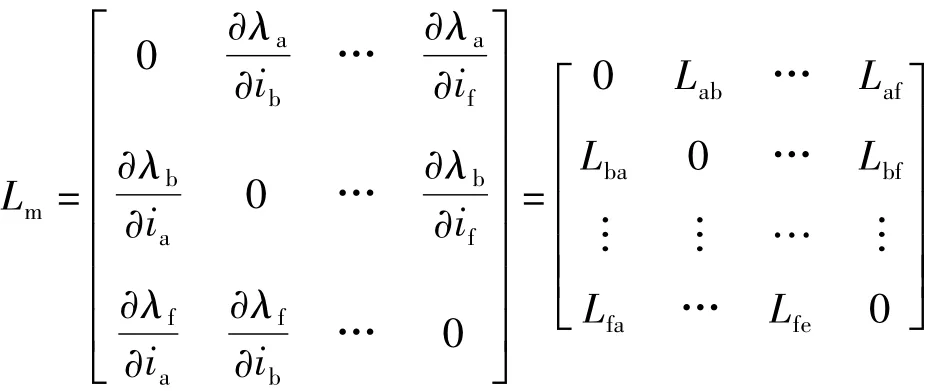
为互感矩阵;

例如:a相感应电压方程式可表示为

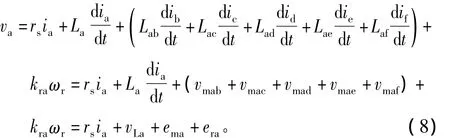
a相等效电路如图8所示，即每相电压包括电阻电压，自感电压，互感电压和由开槽气隙所产生的转子运动感应电压。

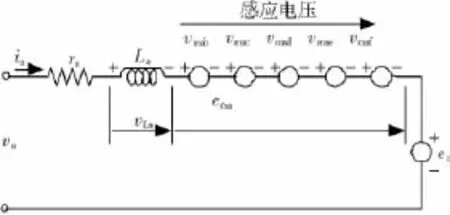
图8 a相的等效电路Fig.8 Equivalent circuit of phase a

定子其中一相的互感电压表示为

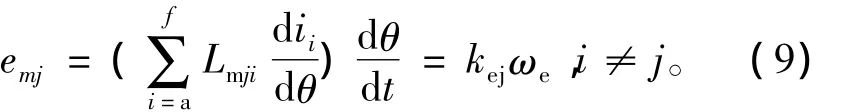
到此为止a相所有的参数已被确定;其他相的参数值和a相都是一样的。由上述分析可知，每相绕组的等效电压方程可以简化如方程(10)所示;相应的等效电路图如图9所示。

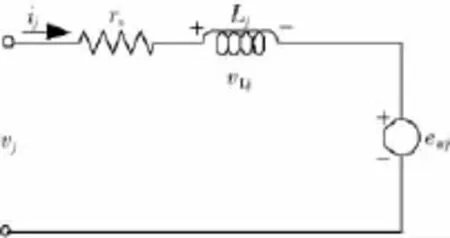
图9 每相绕组的等效电路简化图Fig.9 Per phase simplified equivalent circuit

4 实验验证

用来测试六相感应电机驱动性能实验设置框图如图10所示，主要由六相交流电机、直流电机、六相全桥逆变器和测速编码器等组成。

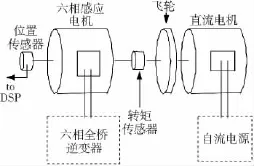
图10 电机实验装置Fig.10 Machine test bed

4.1 气隙磁通密度和励磁电流

利用改进的六相感应电机绕线转子［16］来研究实际气隙磁通密度波形及其幅值大小。为了实际测试气隙磁通密度B，定子3个相邻相经过该接如图11所示。这样连接是为了得到了相电流的配置为:ia=－ic=－2id=IF，(三相电流在t=t1/2处的电流值)。在转子所有相处于开路条件下，以及改变定子励磁电流的情况下，用额定转速为120 r/min的直流电机来驱动六相感应电动机，可以得到转子各相感应电压。定子电流等于3 A时的转子感应电压波形如图12所示。实测波形图12和仿真波形图7相比，结果非常一致。这证实了有限元分析法得到的波形图是正确的。

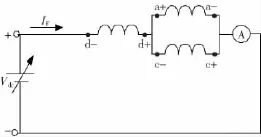
图11 定子相电路连接图Fig.11 Circuit of the stator phase setup

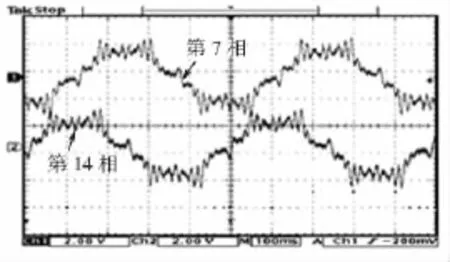
图12 定子磁场静止时开路转子感应电压波形图(第7相到第14相)Fig.12 Measured open-circuit rotor induced voltage waveform(phase 7 and 14)with stator field at standstil

4.2 稳态转矩测试

稳态转矩测试是在额定励磁电流和转子堵转时和某一特定转矩电流情况下进行的。测试结果如图13所示。为了便于比较，理论计算和有限元分析的结果也显示在图13中。

从图13可以看出在理论计算和有限元分析之间有很好的一致性，但实测的转矩与理论分析值相比偏小。后者产生的原因是转子相绕组感应电流与理论分析的波形相比，有一定的差异。此外，滑环与电刷的接触电阻，使得该转子相绕组的感应电流大大降低，对输出转矩产生了负面影响。

从图13可以得到另一个重要结论:输出转矩和六相感应电机驱动器的转矩电流之间存在线性关系。这是非常重要的，因为它表明在六相感应电机驱动控制器的磁动势平衡或零正交磁通量下，电磁转矩与转矩电流能保持线形关系。

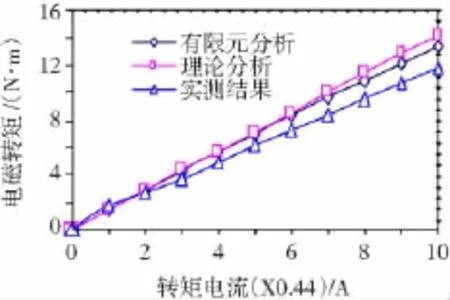
图13 在额定励磁和转子堵转时转矩和转矩电流的关系图Fig.13 Torque versus torque current at rated field current and with a locked rotor

4.3 转矩响应

六相感应电机在阶跃转矩电流信号下的转矩响应是在转子堵转情况下实验的。测试条件为IF=3.5 A和阶跃转矩电流为2.2 A。在阶跃转矩电流信号下的转矩响应如图14所示。

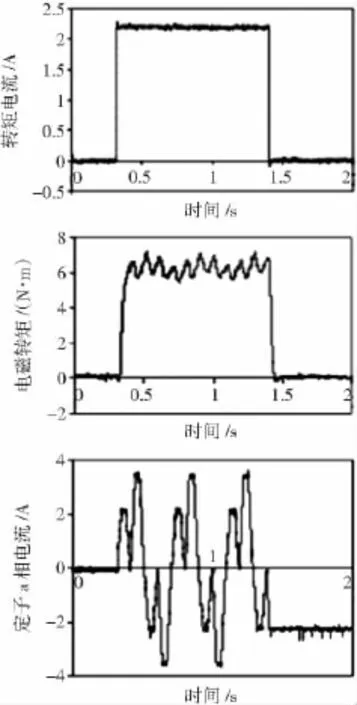
图14 转矩对冲击电流的反应(滤波后)(从顶向下:阶跃电流信号;被测量的转矩响应;被测量的相电流)Fig.14 Troque response to step torque current command(filtered)(from top to bottom:step torque current command;measured troque response;measured phase a current)

从图14可发现，六相感应电机驱动器的转矩响应是很快的。在被测量的转矩波形中，可发现电磁转矩具有一定的脉动。这些测量结果和仿真结果一致的。

5 结论

研究在梯形波相电流驱动下六相感应电机的建模和其驱动器的性能后，可得如下结论:

1)六相等效电路可简化成类似直流电机的励磁电路和电枢电路，这就提供了一种新颖的控制策略。

2)通过研究六相感应电机输出转矩的静态和动态性能，测量结果表明理论分析和有限元分析的结果是一致的。通过测量转子感应电压和感生电流来进一步验证六相感应电机的新颖控制原理。通过实验表明，该梯形波相电流由励磁电流和转矩电流组成，在该梯形波相电流驱动下六相定子绕组可以分为励磁绕组和转矩绕组，模拟直流电机实现励磁磁场和转矩的直接控制而不需要复杂的派克变换。

［1］ TRZYNADLOWSKI A M.Control of induction motor［M］.London:Academic Press，2001.

［2］ NELSON R H，KRAUSE P C.Induction machine analysis for arbitrary displacement between multiple winding sets［J］.IEEE Trans Power App Syst，1973，PAS －93:841 －843.

［3］ LIPO T A.A d-q model for six-phase induction drives［C］//Proc Int Conf on Electrical Machines ICEM.Athens:Greece，1980，2:860－867.

［4］ HADIOUCHE D，RAZIK H，REZZOUG A.On the modeling and design of dual-stator windings to minimize circulating harmonic currents for VSI fed AC machine［J］.IEEE Trans on Ind Appl 2004，40(4):506 －515.

［5］ ZAO Y，LIPO T A.Modeling and control of a multi-phase induction machine with structural unbalance:Part I Machine modeling and multi-dimensional current regulation［J］.IEEE Trans on Energy Conversion，1996，11(3):570 －577.

［6］ ZAO Y，LIPO T A.Modeling and control of a multi-phase induction machine with structural unbalance:Part II Field-oriented control and experimental Verification［J］.IEEE Trans on Energy Conversion，1996，11(3):578 －584.

［7］ LYRA R O C，LIPO T A.Torque density improvement in a sixphase induction motor with third harmonic current injection［J］.IEEE Trans on Ind Appl，2002，38(5):1351 －1360.

［8］ BOJOI R.Digital field-oriented control for dual three-phase induction motor drives［J］.IEEE Trans on Ind Appl，2003，39(3):752－759.

［9］ SINGH G，NAM K，LIM S K.A simple indirect field oriented control scheme for multiphase induction machine［J］.IEEE Trans on Ind Electronics，2005，52(6):1177 －1184.

［10］ JIANG S Z，CHAU K T，CHAN C C.Spectral analysis of a new six-phase pole-changing induction motor drive for electric vehicles［J］.IEEE Trans on Ind Elec，2003，50(1):123 －131.

［11］ 陈林，熊有伦.多相感应电动机调速系统研究与应用［J］.微特电机，2002，30(1):33 －35.

CHEN lin，XIONG Youlun.The research and application for multiphase induction motor speed adjustment system［J］.Small＆ Special Electrical Machines，2002，30(1):33 －35.

［12］ 侯立军，苏彦民，陈林.一种新颖的用于六相感应电机调速系统的空间矢量PWM方法［J］.电工电能新技术，2004，23(1):11－15.

HOU Lijun，SU Yanmin，CHEN Lin.A novel space vector PWM Method for six － phase induction machine［J］.Advanced Technology of Electrical Engineering and Energy，2004，23(1):11－15.

［13］ 侯立军，周玲玲，陈林.六相感应电机调速系统的建模和仿真研究［J］.系统仿真学报，2004，16(6):1249 －1253.

HOU Lijun，ZHOU Lingling，CHEN Lin.Modeling and simulation research of six-phase induction machine drives［J］.Journal of System and Simulation，2004，16(6):1249 －1253.

［14］ AI Yongle，KAMPER M J.Torque performance investigation of double three-phase motor using special current waveform［C］//IPEMC2004.Xi'an China:IEEE，2004，1673 －1678.

［15］ AI Yongle，KAMPER M J.Investigation of air gap flux density and torque performance of six-phase induction Motor with special phase current waveform［C］//ICEMS.Nanjing:IEEE Press，2005，99 －104.

［16］ AI Yongle，KAMPER M J.，LE Roux A D.Novel direct field and direct torque control of six-phase induction machine with special current waveform［C］//IEEE-IAS Annual Meeting 2006，Florida，USA:IEEE Press，2006:98 －112.