模糊灰关联分析方法在故障树分析中的应用

周真， 马德仲， 于晓洋， 樊尚春

(1.哈尔滨理工大学测控技术与通信工程学院，黑龙江哈尔滨150040;2.北京航空航天大学仪器科学与光电工程学院，北京100191)

0 引言

故障树分析法(fault tree analysis，FTA)是1961年由美国贝尔实验室的华生(H.A.Watson)和汉塞尔(D.F.Haasl)首先提出，并应用于民兵导弹发射系统的质量控制。经过多年发展，FTA在对机械系统可靠性、安全性分析和风险评估上得到了广泛应用，已成为一种较为成熟的工程计算方法［1］。

传统的FTA方法存在以下不足之处:首先，传统的FTA方法在对系统的可靠性进行分析时，认为部件只有工作或故障两种状态，不能对系统的可靠性做出更确切或更符合客观实际的评价;其次，传统的FTA方法以布尔代数法为基础，需要精确已知部件故障发生概率和故障事件之间的联系，忽略了环境的模糊性和数据的不准确性会对部件故障概率产生影响，给故障树定量计算带来很大的误差［2］;最后，部件故障概率值的获取和故障事件之间关系的明确需要大量统计数据，对于新研制产品或故障发生概率很低的部件难以获取大量的数据。由于这些问题的存在，导致在分析多状态不确定性复杂系统时，传统的FTA方法难以得到令人满意的结果。

1 故障树方法的改进

1983年，H.Tanaka等人提出模糊故障树方法［3］。该方法针对故障树的顶上事件和基本事件的发生概率，采用模糊概率值取代精确概率值，将模糊数学和经典的事故树理论进行了有效的结合，解决了顶上事件和基本事件的精确发生概率难以确定的问题，在各领域得到了发展和应用［4－5］。近年来，李瑰贤、周继忠等人提出将灰色关联分析方法用于故障树分析过程，解决故障信息缺乏导致的故障事件之间关联不确定性问题，取得了一定的进展［6－7］。

但是，在工程实际中往往在一个信息不完全的问题中存在许多模糊的因素，或是具有模糊因素的一个问题不具备完全充分的资料，即在一个问题中既存在模糊性，又具有灰色性。因此，本文同时考虑系统的模糊性和灰色性，采用灰关联分析方法对模糊故障树进行改进，形成模糊灰关联分析方法。

2 模糊灰色关联分析方法

2.1 建立故障树

首先确定一个最不希望发生的故障事件作为顶上事件(用T表示)，逐步找出各中间故障事件(用A表示)的全部可能起因，并用故障树符号表示各类故障事件及其逻辑关系，直至分析到各类基本事件(用X表示)。

2.2 求故障树的结构函数和最小割集

求故障树的结构函数就是将故障树用简单的数学表达式表示出来，以便于对故障树进行简化，并用数学方法进行运算。具有n个基本事件的故障树的结构函数可表示为:Φ(X1，X2，…，Xn)。

故障事件所组成的集合中全部基本事件都发生时顶事件必然发生，则这个故障集合是故障树的一个割集，若将割集中任意去掉一个基本事件后割集就不成立的故障集合则为最小割集(用F表示)［8］。确定简单故障树的最小割集时，只需将故障树的结构函数展开，使之成为具有最小项数的积之和的表达式，每一项乘积就是一个最小割集。

2.3 确定基本事件的模糊概率

基本事件的精确概率往往难以确定，这里采用模糊数来表示基本事件的发生概率。模糊数有多种形式，如三角形模糊数、梯形模糊数、正态模糊数、LR型模糊数和语言值等。而三角模糊数参照函数处理较方便，代数运算较容易。因此，在模糊故障树分析中采用三角模糊数。一个三角模糊数～p的隶属度函数具有如下形式，即

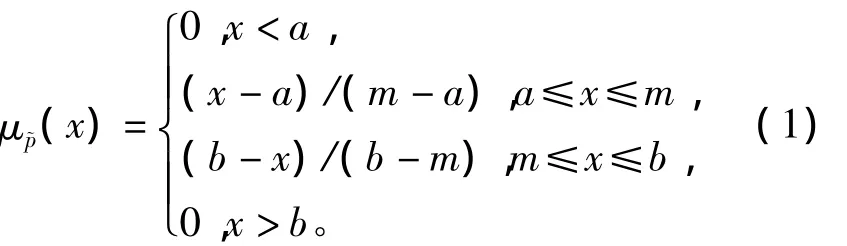
隶属度函数可以通过图1形象的表示出来。

图1 三角模糊数的隶属度函数Fig.1 Membership function of triangular fuzzy number

因此，三角模糊数也可由3个参数 a，m，b表示，记为 ～p=(a，m，b)。

2.4 计算顶上事件的模糊概率

计算顶上事件的模糊概率需要依据三角模糊数的模糊运算法则。故障树的主要逻辑门“与门”、“或门”的模糊算子如下［9］

“与门”模糊算子

“或门”模糊算子

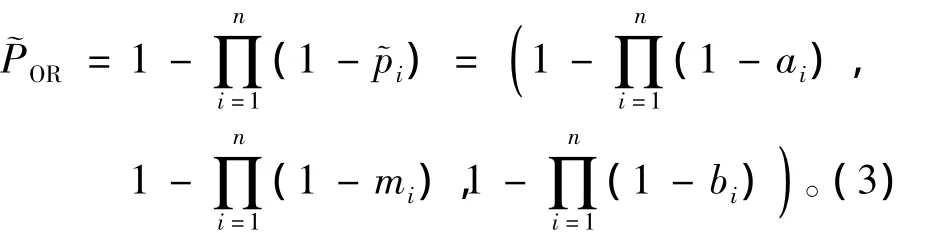
通过以上运算法则可求得顶上事件的模糊概率为

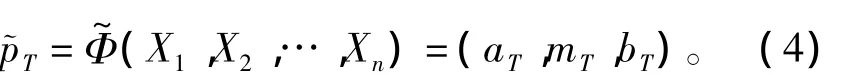
2.5 计算基本事件的模糊重要度

重要度分析是故障树分析的重要组成部分。根据有界闭模糊数中值的定义［10］，这里给出计算模糊重要度的中值法。对于图1，令

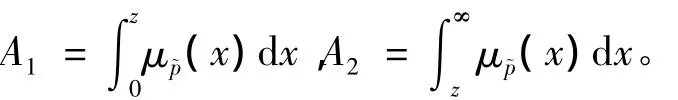
则必然存在一个z点使A1=A2，即以经该点的垂线为分界线，使隶属度函数曲线的左、右两部分积分面积相等，则称z为该模糊数的中值。三角模糊数的中值的计算式为

顶上事件模糊概率(aT，mT，bT)的中值计为zT;基本事件Xi不发生时，顶上事件依然发生的模糊概率表示为

其中值计为zTi。

基本事件Xi的模糊重要度为

2.6 确定参考列和比较列

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之就越小［11］。因此，首先需要确定参考序列和比较序列。

这里把对各基本事件的模糊重要度做均值化处理后作为参考列。

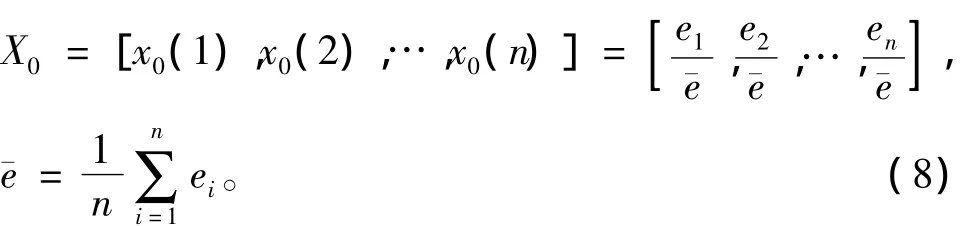
当故障树具有m个最小割集时，可用一个特征向量来代表相应的最小割集，进而构成一个典型故障的特征矩阵

在特征矩阵中，当基本事件Xi出现在最小割集Fk中时，取 xk(i)=1;否则，取 xk(i)=0。

将特征矩阵F中的每一个特征向量作为一个比较列。

2.7 计算关联系数与灰色关联度

参考列中的元素x0(i)与比较列中的元素xk(i)之间的灰关联系数的计算式为

式中

ρ为分辨系数，一般取ρ=0.5。

最小割集Fk的灰色关联度的计算式为

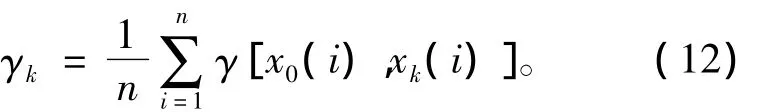
最终，比较m个最小割集的灰色关联度的大小，灰色关联度越大的最小割集所代表的故障模式造成顶上事件发生的可能性就越大;反之造成顶上事件发生的可能性就越小。

3 应用实例

风力发电机作为风能转化为电能的基础设施在整个风力发电系统中有着举足轻重的作用。风力发电机各部件长期工作在野外。由于环境影响因素众多且相互之间作用复杂，导致了风力发电机故障种类繁多，故障原因复杂，故障征兆模糊，故障机理不清，故障数据缺乏等问题，从而使得现场数据带有极大的复杂性、模糊性、不确定性，给故障分析过程造成困难。使用传统的可靠性分析方法难以得到令人满意的结果。

风力发电系统主要包括塔架、风轮、变桨系统、机舱、传动系统、偏航系统、刹车系统、发电机、电气系统、主控系统、传感器等子系统。其中风轮是捕获风能的装置，由叶片和轮毅组成。由于风力发电机长期工作于雨、雪、大风等恶劣环境中，易造成风轮不平衡、浆叶和轮毅的腐蚀、损伤等故障。

本文依据风力发电机的故障统计资料，建立风轮叶片故障的故障树，利用上述模糊灰关联分析方法对故障树进行分析，其过程如下。

3.1 建立故障树

风轮叶片故障树结构如图2所示。

图2 风轮叶片故障树Fig.2 FTA of rotor blades

故障树的顶上事件T表示风轮叶片故障;中间事件A1表示质量不平衡，A2表示空气动力学不平衡，A3表示叶片裂纹损伤;各基本事件的含义如表1所示。

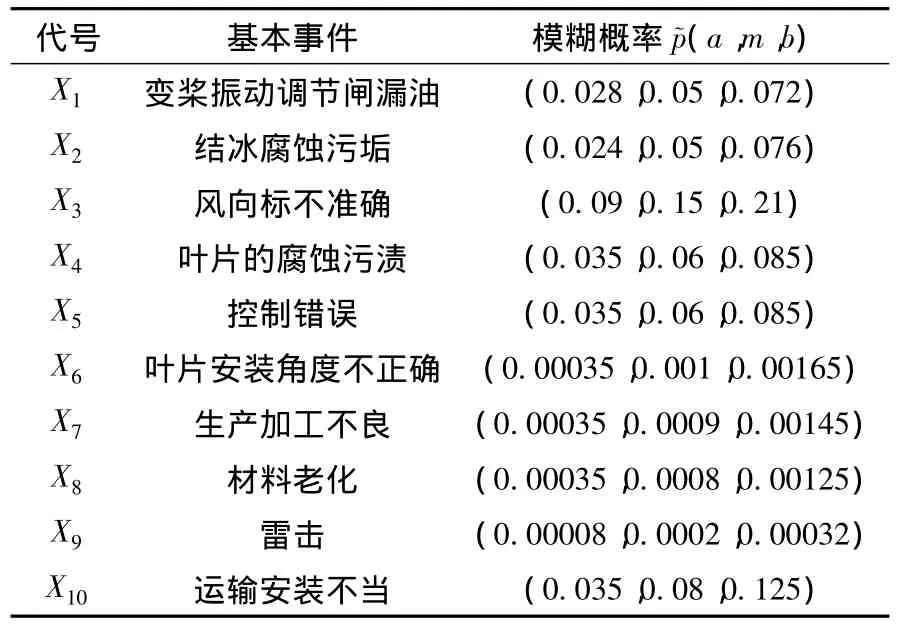
表1 基本事件模糊概率Table 1 Fuzzy probabilities of basic events

3.2 求故障树的结构函数和最小割集

上面故障树的结构函数为

可见故障树的每个基本事件就构成一个最小割集，即

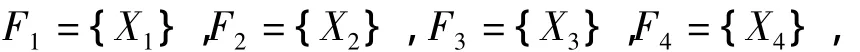
3.3 确定基本事件的模糊概率

根据工程经验，利用三角模糊数来表示各基本事件的模糊概率，如表1所示。

3.4 计算顶上事件的模糊概率

根据故障树的结构函数和三角模糊数的运算法则，计算顶上事件的模糊概率为

～pT=(0.225 095，0.378 201，0.506 067)。

3.5 计算基本事件的模糊重要度

根据式(5)～(7)计算得各基本事件的模糊重要度所构成的集合{e1，e2，e3，e4，e5，e6，e7，e8，e9，e10}={0.032 726，0.032 726，0.109 729，0.039 689，0.039 689，0.000622，0.00056，0.000498，0.000124，0.054069}。

3.6 确定参考列和比较列

根据式(8)确定参考序列，即

根据式(9)确定比较序列，即

3.7 计算关联系数与灰色关联度

根据式(10)和式(11)求得关联系数如表2所示。

表2 关联系数Table 2 Incidence coefficients

根据式(12)求得各最小割集的灰色关联度所组成的集合{r1，r2，r3，r4，r5，r6，r7，r8，r9，r10}={0.757866，0.757866，0.731 167，0.751 827，0.751 827，0.688775，0.688616，0.688458，0.687503，0.74352}。

对各最小割集的灰色关联度进行排序:r1=r2＞r4=r5＞r10＞r3＞r6＞r7＞r8＞r9。该结果反映出了各最小割集所代表的故障模式导致顶上事件发生的可能性的大小。

4 结论

1)本文提出了利用灰关联分析方法对故障树基本事件的模糊重要度进行分析的模糊灰关联分析方法。解决传统的故障树分析方法无法解决的由于故障信息缺乏所导致的顶上事件和基本事件的概率无法确知以及基本事件与顶上事件之间的相互关联难以确定的问题。

2)应用该方法对风力发电机系统的风轮叶片故障树进行分析，对造成顶上事件发生的各种故障模式可能性大小做出判断，找出了风轮系统中变桨振动调节闸漏油，结冰腐蚀污垢等关键故障模式，为处理事故的轻重缓急、控制事故的发生、改进系统可靠性和安全性提供了理论依据。

3)该方法同时考虑系统的模糊性和灰色性，经进一步的研究改进，可用于包括机械系统在内的多状态不确定性复杂系统的可靠性分析。

［1］ 许荣，车建国，杨作宾，等.故障树分析法及其在系统可靠性分析中的应用［J］.指挥控制与仿真，2010，32(1):112－115.

XU Rong，CHE Jianguo，YANG Zuobin，et al.The fault tree analysis and its application in the system reliability analysis［J］.Command Control＆ Simulation，2010，32(1):112－115.

［2］ 姚成玉，张荧驿，王旭峰，等.液压系统故障树分析技术的研究现状与发展趋势［J］.液压气动与密封，2010，(8):19－23.

YAO Chengyu，ZHANG Yingyi，WANG Xufeng，et al.Current research and developing trends on fault tree analysis of hydraulic system［J］.Hydraulics Pneumatics ＆ Seals，2010，(8):19 －23.

［3］ TANAKA H.Fault-tree analysis by fuzzy probability［J］.IEEE Transactions on Reliability，1983，32(5):453－457.

［4］ Renjith.V.R.，G.Madhu，Nayagam.V.Lakshmana Gomathi.Two-dimensional fuzzy fault tree analysis for chlorine release from a chlor-alkali industry using expert elicitation［J］.Journal of Hazardous Materials，2010，183(1):103 －110.

［5］ HONG Yingyi，LEE Lunhui，CHENG Henghsing.Application of fuzzy fault-tree analysis to assess the reliability of a protection system for a switchyard［J］.International Journal of Emerging Electric Power Systems，2008，9(4):1 －6.

［6］ 李瑰贤，于广滨，孙瑜.基于灰色关联的微小型活齿传动模糊故障树分析［J］.中国工程机械学报，2006，4(2):127－132.

LI Guixian，YU Guangbin，SUN Yu.Application of grey－relational theory in fault tree analysis of miniature sine oscillating tooth gear drive［J］.Chinese Journal of Construction Machinery，2006，4(2):127－132.

［7］ 周继忠.灰色关联故障树分析法在基坑工程放坡开挖中应用［J］.土木工程学报，2009，42(8):109－114.

ZHOU Jizhong.Application of gray correlation fault tree analysis for unprotected open cut excavations［J］.China Civil Engineering Journal，2009，42(8):109 －114.

［8］ 阎树田，郭波，崔庆成.基于模糊故障树理论卷板机可靠性分析［J］.机械与电子，2009，(11):23－26.

YAN Shutian，GUO Bo，CUI Qingcheng.Reliability analysis of roll bending machine based on fuzzy fault tree［J］.Machinery ＆Electronics，2009，(11):23－26.

［9］ 李青，陆廷金，李宁萍.三角模糊数的模糊故障树分析及其应用［J］.中国矿业大学学报，2000，29(1):56－59.

LI Qing，LU Tingjin，LI Ningping，Fuzzy fault-tree analysis with triangular fuzzy number and its application［J］.Journal of China University of Mining＆Technology，2000，29(1):56－59.

［10］ Mitauo Y.The median for a L-R fuzzy number［J］.Microelectron.Relia，1995，35(2):269－271.

［11］ 刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.北京:科学出版社，2010:62－63.