基于FPGA的高阶FIR滤波器强抗干扰数据采集系统

唐 博,李锦明,李士照

(中北大学 电子测试技术国家重点实验室，山西 太原 030051)

数据采集系统能实时采集生产过程中的各种数据、参数，成为获取系统工作状态、运行情况的非常重要的手段。近年来，各种应用领域对数据采集系统的性能提出了更加严格的要求：不但要求实现采集关键信息的功能，且对采集系统的抗干扰能力、无用信号的剔除能力提出了很高的要求。特别是在所采集信号被无用信号覆盖或是采集系统工作在具有强干扰的环境下时，如何从采集的数据中提取有用信号，去除干扰信号是现如今数据采集系统的难点和研究的热点。基于FPGA的FIR滤波器由于具有设计灵活、速度快、增益容易控制、稳定性好的优点，逐渐成为数字信号提取的一种非常重要的手段。利用其作为数据采集系统的前端信号处理，已经是高精度和抗干扰数据采集领域的很好的实现方案。

1 FIR滤波器的简介

有限脉冲响应FIR(Finite Impulse Response)滤波器由于其具有良好的线性相位和极高的稳定性，在数字信号处理领域得到了极为广泛的运用。N阶FIR滤波器基本系统函数如式(1)：

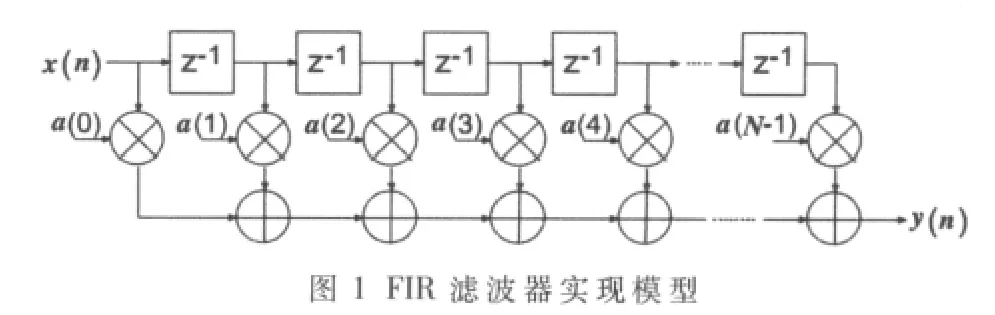
式中：a(i)表示滤波器的系数；x(n)表示带有时间延迟的输入序列，其直接实现模型如图1所示。

由图 1可以看出，FIR滤波器的输出y(n)是由当前输入x(n)到 x(n-N+1)与抽头系数 a(i)的卷积[1]。由于每一次输出要做N次乘法和N-1次加法，所以如果用串行结构来实现，当阶数N较大时，系统的延时就会很大。如今的数字FIR滤波器大体上可以分为基于DSP的FIR滤波器和基于FPGA的FIR滤波器：基于DSP的FIR滤波器实现简单，只需要几条简单的语句就可以实现，大量运用于数字信号处理过程中。但是由于DSP的运算是串行的，所以不可能设计出高阶快速的FIR滤波器。基于FPGA的FIR滤波器是近几年随着FPGA资源的急速增长而发展出来的一种新型的FIR滤波实现方案[2]，它具有可配置性强，灵活多样，速度快，稳定性高的优点，逐渐成为工业控制和航天领域中FIR滤波的首选实现方案。

2 系统实现方案

2.1 总体设计方案

系统采集的模拟信号是带有很大噪声和正弦信号的未解调的微弱电压信号，系统实现框图如图2所示。

系统采集的模拟信号线由信号调理电路进行放大，简单滤波;然后将放大后的模拟信号传送到A/D进行数模转换;最后在FPGA的控制下将数据传送到FPGA内部，处理后传送到PC机进行显示。

2.2 系统硬件实现方案

由于系统采集到的模拟信号是非常微弱的电压信号，因此在进行A/D转换以前，需要设计信号调理电路将电压信号放大，总结以前设计经验，采用低失调、低噪声的AD620芯片进行前级的高精度电压放大，放大后的信号经过OPA2277运放跟随最终输出给A/D。信号调理电路单路电路图如图3所示。

AD620放大倍数由 VR1调节,放大倍数由式(2)计算：

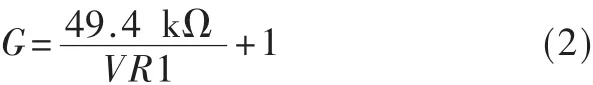
调节滑动变阻器,将OPA2277的输出电压控制在0～5 V之内，虽然加入了一个简单的有源RC低通滤波，但是信号有用成分仍然被噪声和叠加的高频正弦波所覆盖。

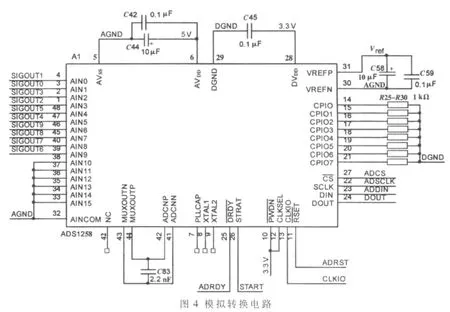
放大后的电压信号虽然幅值在0～5 V之内,但是淹没在其中的关键信号却仍然只有几毫伏，如果用普通的低精度ADC进行模数转换，由于ADC的转换误差正好和关键信号相差不大，使得转换后的数字信号中引入了相对大的误差。即使后续滤波，得到的也是叠加了误差的关键信号，无法实现高精度采集并解调。因此采用TI公司的24位16通道串行高精度ADC芯片ADS1258进行模数转换。电路图如图4所示。

ADC的主时钟采用FPGA主时钟分频后的16 MHz方波信号，选择AIN0～AIN9通道作为模拟信号输入，内部采用自动扫描方式。ADC的控制端口都接到了FPGA的通用I/O口。 ADC内部寄存器配置数据从FPGA通过ADC的SPI口写入。配置数据在SPI时钟的上升沿写入，转换后的数据在SPI时钟的下降沿读出。内部寄存器配置情况如表1所示。

本系统的主控制器采用XILINX公司的SPARTAN3E系列的FPGA XC3S200E，这款芯片在资源上能满足系统的要求，而且最重要的是在开发环境ISE 9.1以后的版本中，对于SPARTAN3E系列的芯片系统都自带了功能强大的 FIR滤波器 IP核，这样方便设计高速可靠、占用资源少的FIR滤波器。数据传送到上位机使用CY7C68013，由于这方面的设计不是本系统的重点，因此不再累述。

表1 内部寄存器配置情况

2.3 系统程序设计

程序设计是本系统的关键所在，区别于以往系统的关键之处就是高精度ADC的使用和创新性的FIR滤波的引入,使得采集系统具备了超高精度和强抗干扰的能力。

ADS1258是一款多通道串行ADC，由于其控制方式是向其内部寄存器写入一定配置数据来完成A/D转换，所以其使用较为灵活。可配置的波特率及斩波功能也使器件的性能更加突出。器件控制流程如图5所示。

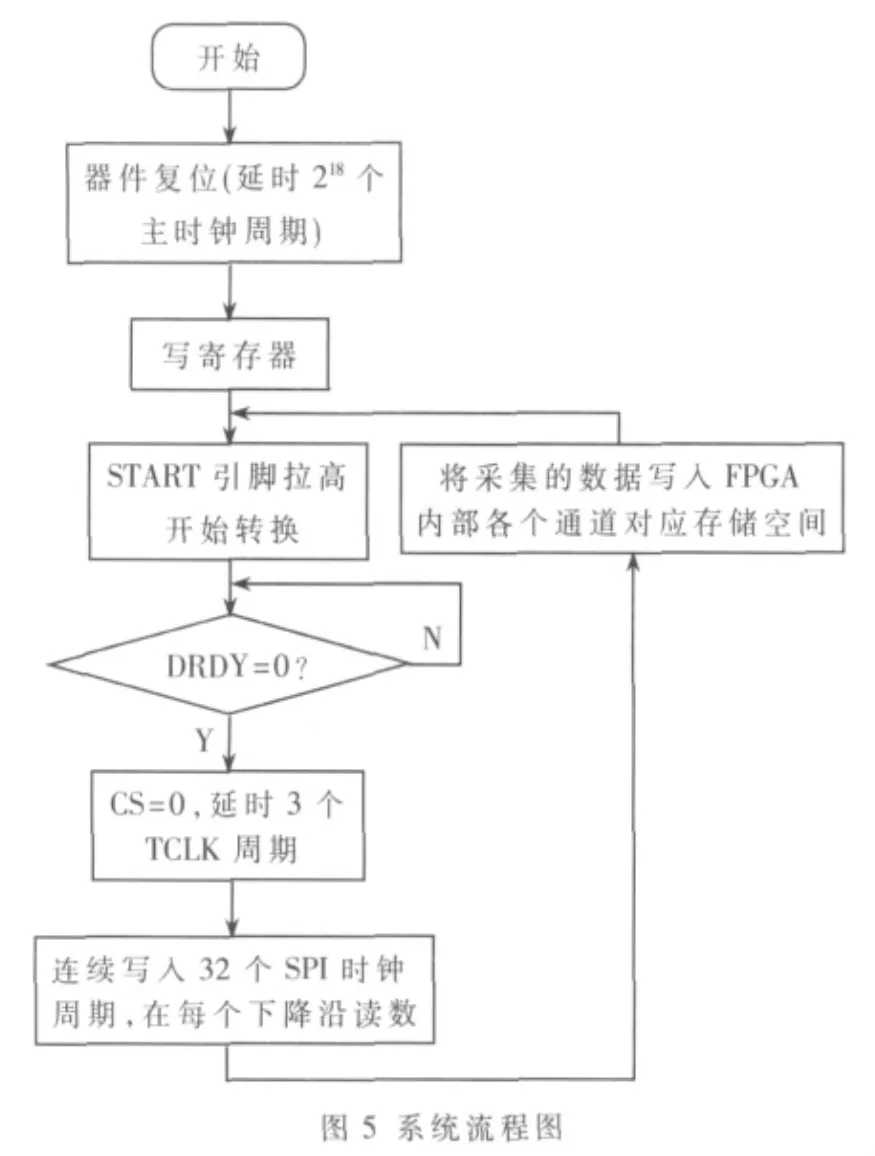
ADC的读写时序特别重要，所以必须按照芯片资料将各个状态之间转换的延时控制好，既不影响转换周期也能保证结果的正确。器件上电后的218个TCLK周期的延时必须保证，否则虽然芯片也能工作，能进行A/D转换，但是写寄存器命名无法使用，无法将系统需要的配置数据写到各个寄存器。在系统开发的前期，由于忽略了这个长时间的复位时间，导致写命令一直无法正确执行，后来加上复位延时后，ADC工作正常，寄存器数据能顺利写进去。每完成一次转换，能从芯片SPI口读出32位有效数据[3]，数据格式如表2所示。

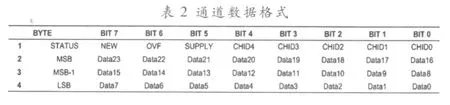
数据低24位为有效A/D数据，高8位为状态和通道标志位,NEW位指示通道数据是否更新，NEW=1代表通道数据相对前一次读取已经更新，NEW=0代表未更新，这样通过判断NEW的值可以防止重复读取同样的数据。OVF位和SUPPLY位分别指示通道端口电压和供电电压是否正常。CHID4～CHID0用来判定读出的数据是属于哪个通道。通过把不同通道的低24位数据写入FPGA不同的存储空间，为接下来的FIR滤波做准备。

FIR滤波器采用系统自带的IP核来开发，这样可以保证FIR滤波器的可靠性并大大缩短开发周期。滤波系数采用Matlab的滤波器设计工具FDATOOL来产生数据。由于系统设计的是超高FIR滤波器，因此系数的生成也需特别注意，并进行一些特定的计算。下面介绍系数的生成办法。在Matlab主界面输入FDATOOL命令，调用FDATOOL工具并设置好滤波系数[4]。由于ADC的采样频率为23.7 kS/s,因此滤波器的采样频率必须大于23.7 kS/s，设置为50 kHz。由于需要采集的关键信号的频率低于100 Hz，因此设置截止频率为200 Hz。之后，将数据导入到Matlab中，得到的数据全为小数，默认保留了小数点后面四位。

由于FPGA不能直接做浮点运算，因此必须将系数整型化，整型化的好坏直接影响滤波的精度[5]。当系数整型化后的系数精度不够时,由于是200阶的高阶滤波，哪怕一点的系数误差，都会累积起来反应在滤波结果上。经过反复试验和研究，发现当FIR滤波器的阶数到200时，整型化滤波系数必须将FDATOOL的值乘以220以上，上文所述滤波系数其实只是截取了小数点后面的四位，如果只将系数乘以104，则小数点4位以后的值便人为忽略了，这在高阶FIR设计时会带来极大误差，造成滤波器不可用。通过观察FDATOOL生成系数的格式，发现其为32位浮点型，其表示精度远远大于小数点四位。在Matlab中输入如下命令：

coe=Num*16777216;

coe=round(coe);

fid=fopen(′fir300.txt′,′wt′);

fprintf(fid,′%d ′,coe);

fclose(fid);

以上语句将系数扩大了224倍,然后将系数取整，并以10进制的格式保存到一个TXT文件中，通过手动修改TXT文件内容满足ISE中系数文件COE的格式要求，最终将TXT文件的后缀名改为.COE[6]，至此系数文件已经生成好了。接下来便是在ISE中调用IP核设计高阶FIR滤波器，具体步骤本文不再阐述。设计关键参数如表3所示。

3 系统实验结果

通过信号程序产生一路带有很大噪声的正弦信号输入到FPGA进行处理，将处理前和处理后的信号都发送到上位机进行画图和频谱分析，得到如图6结果：其上半部分是输入的带噪声的信号，下半部分是经过滤波后得到的信号。

表3 滤波器设计参数

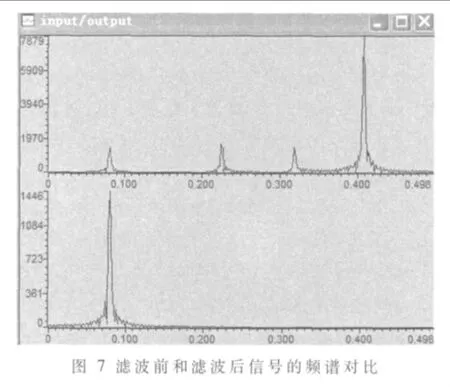
从图6可以看出，由FPGA设计的高阶FIR滤波器良好地实现了有用信号的提取，输入信号中的噪声衰减到几乎为零，即融入了FIR滤波器的本系统具有强抗干扰并同时解调信号的能力。图7是滤波前和滤波后采集到信号的频谱分析图。

图7可以看出，滤波后系统良好地提取出了频率为0.08 kHz的信号， 而频率为 0.23 kHz、0.33 kHz、0.41 kHz的高频干扰信号被削减到了几乎为零,很好地实现了100 Hz内的信号高精度解调。

具有FIR滤波功能的数据采集系统较过去的单一采集系统有很大的进步。高阶FIR滤波器的引入使得本采集系统集抗干扰和解调信号于一体，能适用于各种具有强干扰或者叠加大量无用信号的数据采集场合。

[1]赵岚，毕卫红，刘丰.基于 FPGA分布式算法 FIR滤波器设计[J].电子测量技术，2007,30(7)：101-104.

[2]张维良.高速并行FIR滤波器的FPGA实现[J].系统工程与电子技术，2009,31(8)：1819-1822.

[3]TI.ADS1258 DATASHEET:30-40.

[4]孙耀其.基于MATLAB和FPGA的FIR数字滤波器设计与实现[J].通信与信息技术，2008（11）:89-92.

[5]徐峰，禹卫国，唐红.基于FPGA的流水线分布式算法的FIR滤波器的实现[J].电子技术应用，2004,30(7):70-73.

[6]XILINX.XILINX FIR_compiler_ds534:17-35.