汽车车身冲压件拉延方向自动确定算法研究

胡新阳

（沈阳职业技术学院，沈阳 110045）

0 引言

汽车冲压件是构成非承载式车身的主要组成部分，因此，能够制造出符合要求的汽车冲压件是影响汽车制造质量的重要因素。为了提高汽车冲压件的制造质量，通常在实际拉延进行前需要对设计好的模具进行成形性能仿真。拉延模具成形性能仿真前最重要的一项内容是确定冲压件的冲压方向。拉延方向能够影响成形过程中板料的流向和流速，是决定是否可以生产出合格冲压件的主要因素。另外，拉延方向还是拉延模具结构设计和后续工艺的重要设计依据。传统的拉延件的冲压方向通过不断旋转零件，直到获得满足各项拉延成形准则为止。这种确定冲压方向的方法完全依靠技术人员的经验，确定过程不但费时、费力，更重要的是在可行域内难以获得最优结果。国内的诸多学者对如何自动确定汽车冲压件拉延方向进行大量研究，研究结果主要是借助冲压件的二维截面信息确定拉延方向可行域，在已知可行域内进拉延方向的优化。但应用结果表明，采用二维信息代替冲压件三维实体的转化过程会出现数据“迷失”的情况，这将会导致可行域的缩小，最终导致丧失最优解的情况。丢失最优解的概率虽然很小，但仍需要避免。为改善传统算法的弊端，提出了利用汽车冲压件前处理的网格信息，在三维空间确定单位球内的拉延方向可行域，在可行域内借助遗传算法计算冲压件在待定拉延方向垂直面上的投影面积，并确定与最大投影面积相对应的拉延方向为最优。测试结果表明，汽车冲压件拉延方向自动算法计算过程无需手动干预，能够自动获得最优拉延方向，而且具有精度高、速度快和鲁棒性好等优点。

1 拉延方向优化模型建立

1.1 拉延方向优化模型的约束确定

为了能够有效的确定拉延方向优化模型，首先需要确定优化模型的约束条件，约束条件的确定原则包括以下四个方面：

1）保证拉延模具的凸模能够顺利的进入凹模。当汽车冲压件前处理网格单元的法线与待定拉延方向的夹角务必小于90°，否则将出现凸模无法进入凹模的情况。

2）保证凸模与板料初始接触面积尽可能大。较大的接触面积会使拉延过程平稳且应力分布均匀。

3）冲压件的拉延极限深度尽可能小。较大的拉延深度将会导致破、皱、薄等缺陷。

4）冲压件的各向拉延深度尽可能均匀。均匀的拉延深度可以保证变形量均和进料阻力平均，利于拉延出合格的零件。

1.2 拉延方向优化目标函数

根据汽车车身冲压件CAD零件的网格数据节点确定零件的几何中心，以此中心作为局部坐标系的原点。在拉延方向可行域的范围内随机设定拉延方向Zi(i0,1,…,n)，垂直于拉延方向生成系列与零件相交的等距平面zj(j=0,1,…,m)，截面间距的经验值约为5-10mm，其中，截面z1适合零件总高的1/30为宜。截面分布示意图，如图1所示。

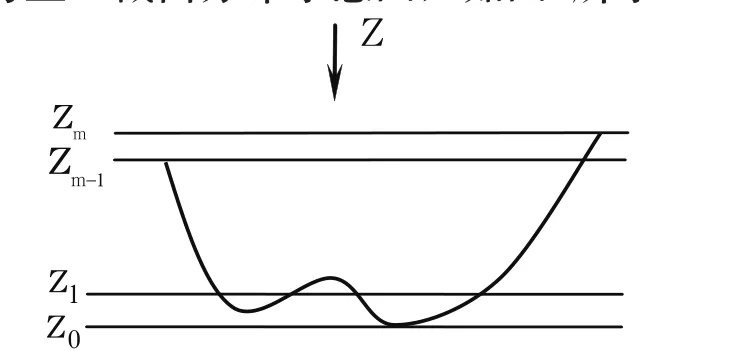
图1 零件截面位置示意图

可行域内车身冲压件的拉延方向Z的约束条件及相关函数如下：

1）拉延开始时，凸模表面与成形板料的接触面积尽可能大。函数表达为：其中，Si为冲压件网格单元i=(1,2,…,k)投影在截面Z0上的面积值。

2）拉延过程中，冲压件不同方向拉延深度尽可能均匀。函数表达为：设f3(Z)=min(zn-zn-1)。

3）拉延结束时，冲压件的拉延深度尽可能浅。函数表达为：f2(Z)=min(zn-zn-1)。

车身冲压件拉延方向优化属于多目标优化问题，需将分散约束函数统一为单目标函数。采用常用的约束函数最大化的方法对约束函数进行转化。设F2(Z)=max[C-f2(Z)]；

F3(Z)=max[C-f3(Z)]，式中，C为远大于拉延极限深度的任意整数，经验值通常设定C＝500mm。考虑各约束函数的权重，将汽车车身冲压件拉延方向目标函数转化为单目标优化函数。加权后的优化模型如下：wk为各约束函数的权重系数。为了能够客观、真实的反应各约束函数偏离最优值的合理分散程度，权重系数采用克雷若诺夫斯基方法，设定为wk=1/maxFi(Z)。式中，

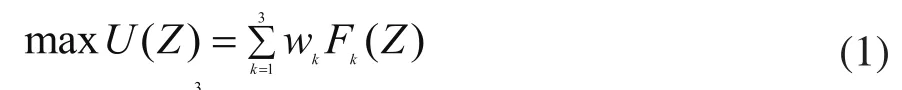
2 算法介绍

2.1 拉延方向可行域

汽车车身冲压件拉延方向额可行域的约束条件为拉延方向单元法线的夹角小于90°，这种约束条件在行业内称之为拉延方向无“负”角。拉延方向无“负”角在可视为在几何上拉延方向与网格单元的法线夹角小于π/2，数学解析为f(Z,ni)=cosαi≥0，式中，ni为网格i的法线方向，αi为拉延方向Z与网格ni的夹角(i=1,2,…,m)。

以局部坐标系原点为球心，建立拉延方向可行域单位矢量球面。

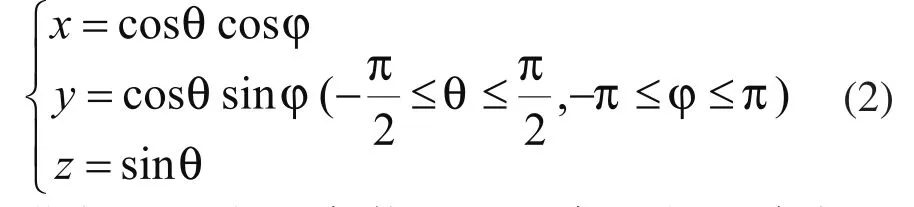
依据无“负”角的拉延方向可行域确定规则，在拉延方向可行域单位矢量球面上，任何网格的法线都有对应的拉延方向可行域矢量半球面。拉延方向可行域矢量球面示意图，如图2所示。网格A的法线方向nA对应的拉延方向可行域是RA半球面，网格B的法线方向nB对应的拉延方向是RB半球面，RA∩RB对应的是基于法线方向nA和nB的拉延方向可行域。依次类推，可以获得所求汽车车身冲压件上所有网格法线方向对应的拉延方向可行域球面，所有拉延方向可行域的交集R就是整个冲压件拉延方向的可行域。

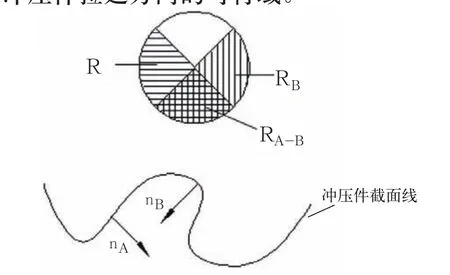
图2 冲压方向可行域示意图

2.2 构造遗传算法

遗传算法对于可行域离散的单目标优化具有很强的适应性，其数学表达形式通常为：

式中，F(x)为为待优化的目标函数，自变量x表示为矩阵形式x=[x1,x2,…,xn]T，R为自变量的可行域（约束条件集）。

采用二进制形式对拉延方向变量Z进行编码，编码区间由π/2-(-π/2)=π与π-(-π)=2π构成。优化精度设定为8位小数，种群N=20，个体变异和染色体交叉按照轮盘概率方式产生。

根据设定的基于遗传算法的汽车车身冲压件拉延方向优化结构，编制程序求解最优拉延方向。遗传算法的程序结构体设置如下：

3 算法流程

拉延方向自动算法程序流程图，如图3所示。

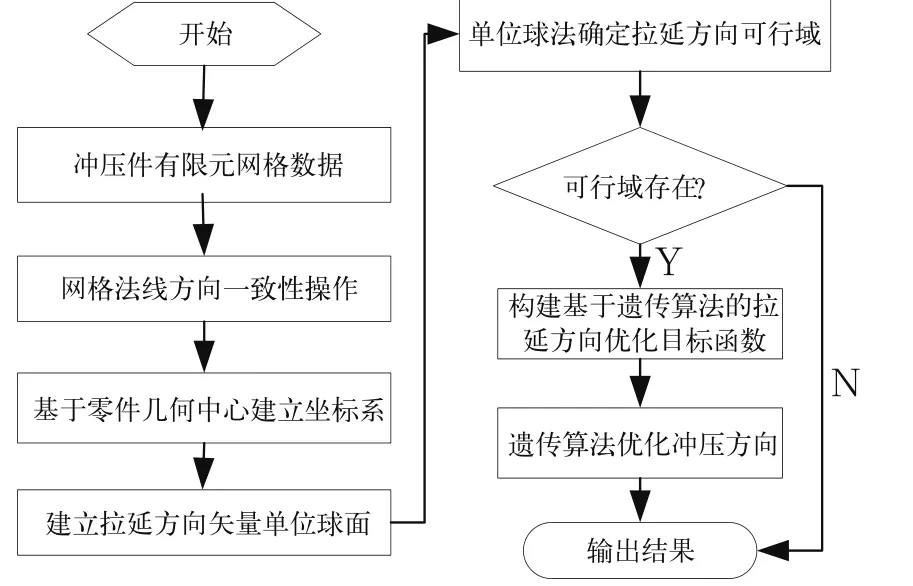
图3 拉延方向自动算法程序流程图

4 实例验证

某厂新开发轿车的右侧围结构复杂，拉延方向对成形质量具有较大影响。如果拉延方向确定不合理将会导致成型后的侧围出现局部的打折、起皱和破裂的情况，甚至会导致零件作废。

对测试的汽车右侧围进行网格划分，划分网格后的汽车侧围，如图4所示。采用遗传算法对拉延方向目标函数进行优化，优化后的最优拉延方向，如图5所示。根据算法获得的拉延方向生产轿车侧围符合设计指标，生产的轿车右侧围，如图6所示。

应用C++编程，ACIS开发平台实现的拉延方向自动算法采用 Pentium IV 2.4G处理器，内存 1G工业计算机平台运行拉延方向优化算法程序，算法总计用时 2.17s，运算速度符合工程计算要求。

图4 某轿车右侧围网格划分图

图5 最优拉延方向示意图

图6 某轿车合格的右侧围冲压件

5 结论

汽车车身冲压件拉延方向自动确定算法采用零件网格法线方向与拉延方向夹角小于90°为判据，以能够获得合格质量冲压件为目标函数，

建立遗传算法优化目标函数。在单位球面法确定的拉延方向可行域内自动获得最优拉延方向。算法能够准确、快速、自动的获得最优的汽车冲压件拉延方向。算法能够自动完成、不需要手动干预。算法程序稳定性好、具有很强的鲁棒性。

[1] 崔令江.汽车覆盖件冲压成形技术[M].北京:机械工业出版社,2003.

[2] 李硕本.冲压工艺理论与新技术[M].北京:机械工业出版社,2002.

[3] 刘君,江仁华.冲压件拉延方向分析方法及应用[J].塑性工程学报,2008,13(4):113-118.

[4] YANG Yu.,Shi L.,Hou J.H.Optimization of stamping direction bases genetic algorithms for automobile panels[J].Computer Integrated Manufacturing Systems.2007,23(1):45-51.

[5] Firat Mh.Computer aided design of sheet metal forming processes: Stamping die design[J].Materials&Design,Volume 29,Issue6,2009,Pages 1288-1293.

[6] Foud EI.K.I,Marc I.AMBRIKS.New requirements development in sheet metal stamping simulation.Proceedings NUMISHEET'02 jiu Island,Korea,2007,12 445-457.

[7] 陈国良,王煦法,庄镇泉.遗传算法及其应用[M].北京:人民邮电出版社,2001.