周期性电压闪变信号数学模型频率特性分析

于静文，薛 蕙，温渤婴

（中国农业大学信息与电气工程学院，北京100083）

随着电力系统冲击性负荷的增加，电网中存在的电压波动和电压闪变也日趋严重，电压波动与闪变已经成为衡量电能质量的主要指标之一。研究电压闪变，积极采取措施以保证电能质量已成为当前供用电的一项重要而紧迫的任务［1］。

闪变通常是指人眼对由一定频率的电压波动所引起的照明异常而产生的直观视觉感受。根据扰动原因的不同，闪变有周期性和非周期性之分，其中对人们生产生活影响较大的为周期性电压闪变。周期性闪变信号的数学模型是以工频电压为载波，其电压的方均根值或峰值受到以电压波动分量为调幅波的调制［1］。而电压中的波动信号往往被认为是电压的包络信号，即调幅波信号。通过对闪变实验的研究发现，人对照度波动的最大觉察频率范围是从0.05Hz到35Hz。因此目前对于闪变的研究主要集中于频率从0.05Hz到35Hz的调制信号产生的闪变［1～11］。

本文在国际电工委员会IEC（International Electrotechnical Commission）推荐闪变仪设计原理的基础上，研究了周期性闪变调制信号模型的频率特性。得出结论：在周期性电压闪变信号的数学模型中，电压波动分量不一定等于调幅波分量；不同频率调幅波产生电压波动的成分不同；频率大于50Hz，甚至是频率大于100Hz的调幅波信号也可能会产生频率范围0.05～35Hz的电压波动，从而产生明显的闪变。

1 IEC推荐的闪变测量原理

通常将电压波动看成以工频电压为载波，其电压的方均根值或峰值受到以电压波动分量为调幅波的调制。对于任何波形的调幅波均可看作是由各种频率分量合成。为使分析简化而又不失一般性，可以分析仅含单一频率的调幅波对工频载波的调制，并设载波幅值为1。调制波解析式的一般表达式为

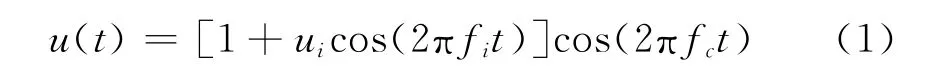
式中：ui为调幅波的幅值；fi为调幅波的频率；fc为电网电压的额定频率，fc＝50Hz。

为使电压波动与闪变的测量方法与标准一致，1986年国际电工委员会根据国际电热协会的推荐，给出了闪变仪测量原理和设计规范，我国国家标准在参考了IEC标准后推荐采用的闪变仪简化原理框图如图1所示［1］。

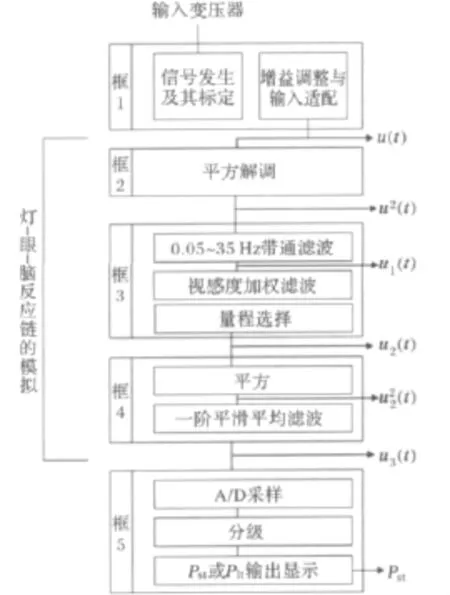
图1 闪变仪的简化原理框图Fig.1 Simplified block diagram of flicker instrument

图1给出的闪变测量环节总体上可分为3部分：第一部分为电压输入适配调整，由图1中框1组成；第二部分模拟视觉系统模型，即灯－眼－脑反映链的频率响应特性，主要由图1中的框2、框3和框4组成；第三部分为测量到的瞬时闪变度的统计分析，由框5组成。

框2模拟灯的作用和特性通过平方解调器分离出与调幅波成比例的电压波动量。该量反映了灯照度变化与电压波动的关系，可采用被测信号自乘求平方来实现。由于人对照度波动的最大觉察频率范围是从0.05Hz到35Hz，因此平方信号中只有频率范围从0.05Hz到35Hz的成分才会产生闪变。因此框2的输出要通过一个通带频率为0.05 Hz～35Hz的带通滤波器，即只有通过0.05～35 Hz带通滤波器输出分量才会引起闪变。下一节将根据上述IEC推荐的闪变测量原理来研究电压闪变信号数学模型频率特性。

2 电压闪变数学模型频率特性研究

设输入电压信号如式（1）所示，自乘求平方后得到电压平方信号u2（t）。

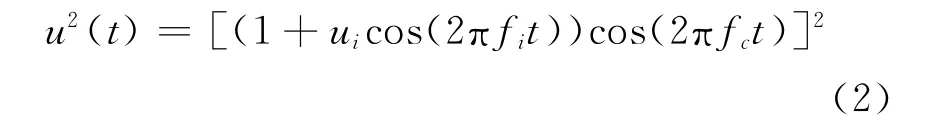
为了分析u2（t）的特性，把u2（t）可按其频率特性分为5部分E1～E5。

即令

式中

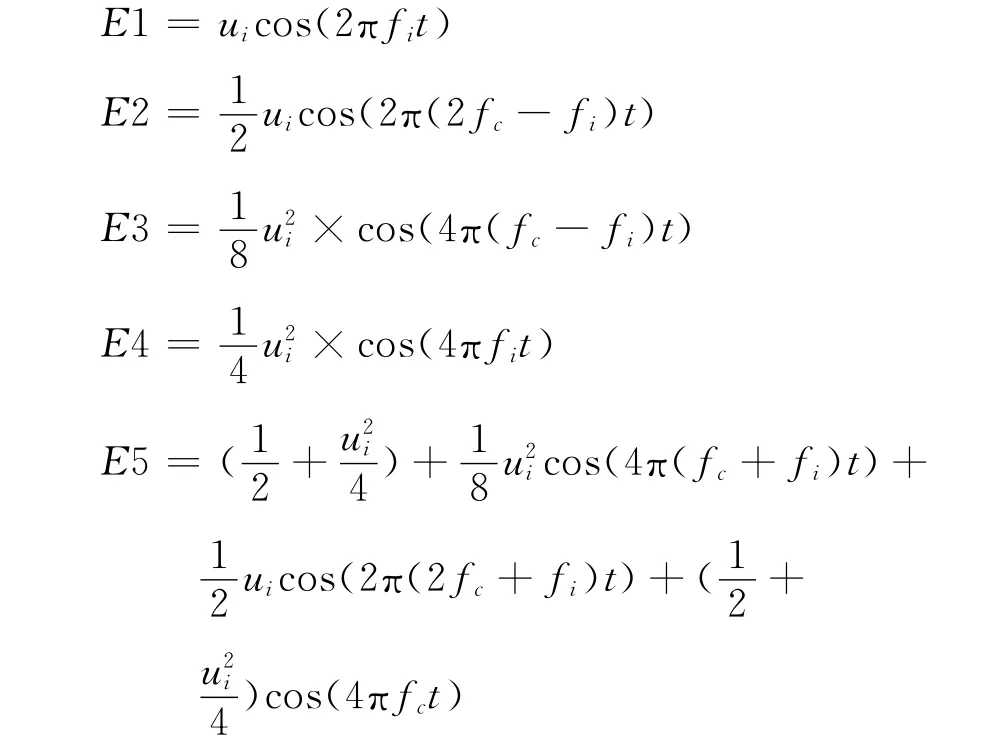
通过0.05～35Hz的带通滤波器后，E1－E5各个部分的频率特性分析如下：

（1）E5是在带通滤波器通带以外的部分。

（2）如果E1在通带范围0.05～35Hz内，则0.05≤｜fi｜≤35Hz⇒0.05≤fi≤35Hz。

（3）如果E2在通带范围0.05～35Hz内，则0.05≤｜2fc－f｜≤35Hz⇒65≤fi≤99.95Hz或100.05≤fi≤135。

（4）如果E3在通带范围0.05～35Hz内，则0.05≤｜2fc－2fi｜≤35Hz⇒37.5≤fi≤49.975 Hz或50.025≤fi≤67.5。

（5）如果E4在通带范围0.05～35Hz内，则0.05≤｜2fi｜≤35Hz⇒0.025≤fi≤17.5Hz。

综合上述分析，调幅波频率fi与0.05～35 Hz带通滤波器输出信号u1（t）关系如下：

（1）当0.025＜fi＜0.05Hz

（2）当0.05＜fi＜17.5Hz

（3）当17.5＜fi＜35Hz

（4）当37.5≤fi≤49.975，50.025≤fi≤65

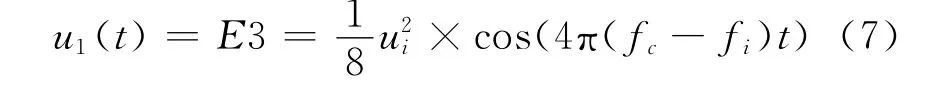
（5）当65＜fi＜67.5Hz

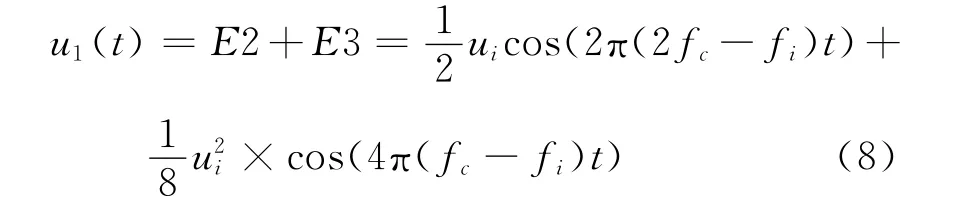
（6）当67.5≤fi≤99.95Hz或100.05≤fi≤135

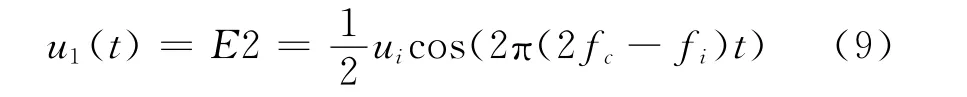
调幅波频率fi与带通滤波器的输出，即影响闪变值的电压波动分量关系见表1。

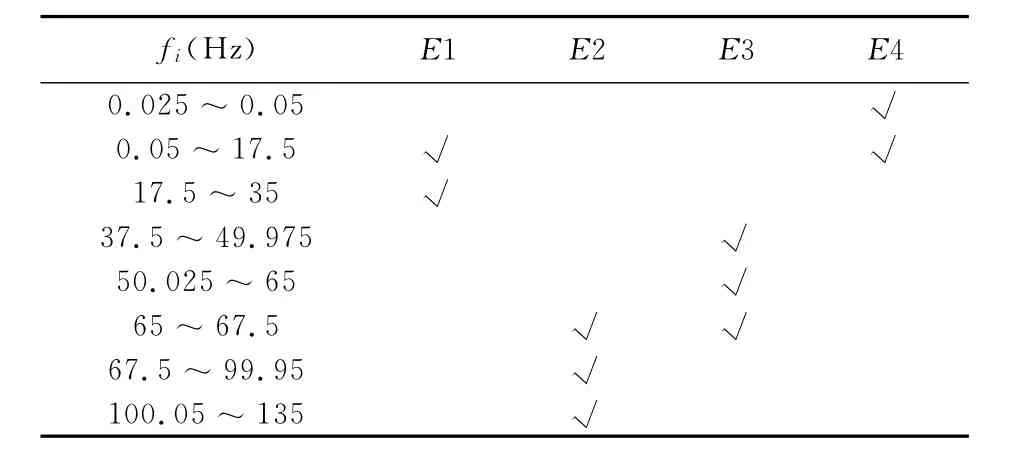
表1 调幅波频率fi与带通滤波器输出u1（t）所含分量关系Tab.1 Relationship of fiand band－pass filter output signal u1（t）

由表1可知，带通滤波器的输出，即影响闪变的分量不仅包含E2，而且可能包含E1、E3和E4。因为一般ui≪1，由式（3）可得E1、E2的幅值往往远远大于E3、E4的幅值，因此E1、E2往往是影响闪变的主要分量。由表1可见，当调幅波频率fi在（0.05，35）Hz，（65 ～ 99.95）Hz 和 （100.05 ～135）Hz范围内时，带通滤波器的输出包含E1或E2分量，因此在这个频率范围内均有可能产生明显闪变。

如果ui的值较大，则E1、E2、E3、E4都会影响闪变。当fi∈ （0.05 17.5）Hz，闪变主要受E1和E4分量影响，而不是只受E1影响。当fi∈（37.5 65）Hz，闪变主要受E3影响，也会产生闪变。

从上述分析可见：频率大于50Hz，甚至频率大于100Hz的调幅波信号也可能产生频率0.05～35Hz的电压波动，即也会产生明显闪变。

3 仿真实验

为验证本文的结论，对含有不同频率调幅波的电压信号做仿真分析。电力系统基波频率为50Hz。

（1）fi＝10Hz时被测电压信号为

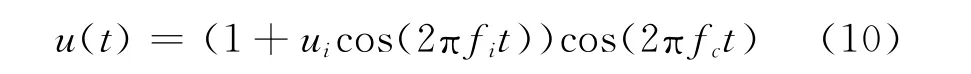
式中ui＝0.1，fi＝10Hz，fc＝50Hz。

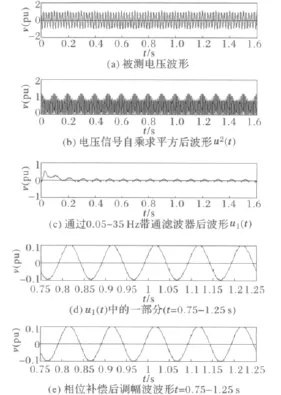
图2 调幅波频率为10Hz的试验波形（1）Fig.2 Test waveforms with a modulation frequency of 10Hz（1）

被测电压波形，自乘求平方后波形，通过0.05～35Hz带通滤波器后波形如图2所示。图2（c）是0.05～35Hz带通滤波器输出波形。为了更清楚地观察通过带通滤波器后的波形，图2（d）截取了图2（c）中t＝0.75～1.25s时段的波形，图2（e）是相位补偿后调幅波的波形。从图2（d）和（e）可以清楚地观察通过0.05～35Hz带通滤波器提取的电压波动信号与相位补偿后调幅波信号基本一致。实验结果符合式（5）结论：fi∈ （0.05 17.5）Hz，所以带通滤波器输出主要包含E1和E4。又由于ui＝0.1，由式（3）可知当E4≪E1时，带通滤波器提取的电压波动信号与E1，即与调幅波信号基本一致。

如果把调幅波的幅值增加到0.5，得到图3。图3（d）和（e）存在较大的差别。这是由于不满足E4≪E1，所以带通滤波器提取的电压波动信号与调幅波信号E1存在明显误差，这个误差是由E4造成的，因此在这种情况下，如果把调幅波信号看作是影响闪变的电压波动信号，就会产生较大的误差。

图3 调幅波频率为10Hz的试验波形（2）Fig.3 Test waveforms with a modulation frequency of 10Hz（2）

（2）fi＝20Hz时被测电压信号为

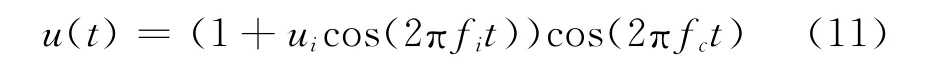
式中ui＝0.1，fi＝20Hz，fc＝50Hz。

被测电压波形，自乘求平方后波形，通过0.05～35Hz带通滤波器后波形如图4所示。图4（c）是0.05～35Hz带通滤波器输出波形。图4（d）截取了图4（c）中t＝0.75～1.25s时段的波形，图4（e）是相位补偿后调幅波的波形。从图4（d）和（e）中可以清楚地观察通过0.05～35Hz带通滤波器提取的电压波动信号与调幅波信号基本一致。实验结果符合式（6）结论：因为fi∈ （17.5 35）Hz范围，所以带通滤波器输出只包含E1。所以带通滤波器提取的电压波动信号与E1，即与调幅波信号一致。

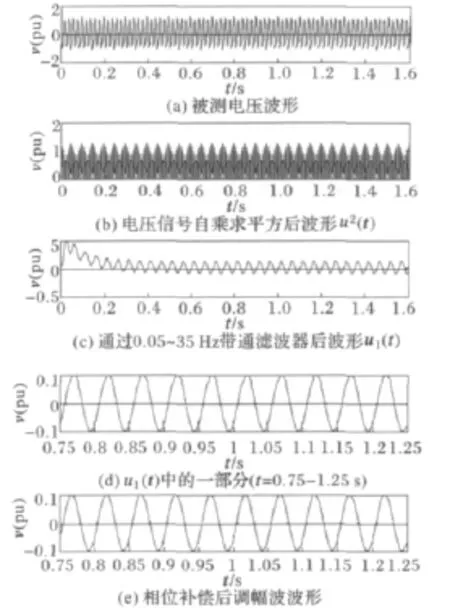
图4 调幅波频率为20Hz的试验波形（1）Fig.4 Test waveforms with a modulation frequency of 20Hz（1）

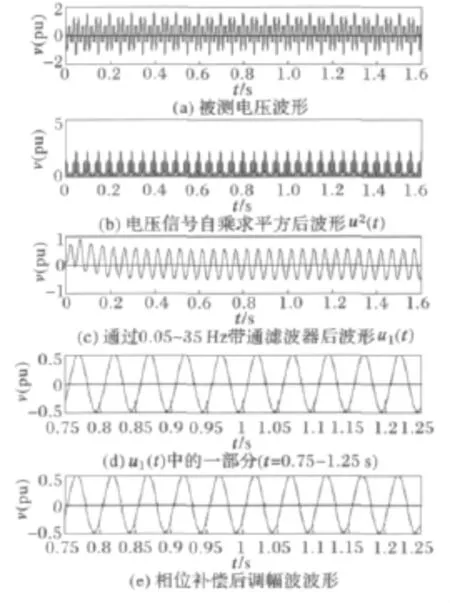
图5 调幅波频率为20Hz的试验波形（2）Fig.5 Test waveforms with a modulation frequency of 20Hz（2）

如果把调幅波的幅值增加到0.5，得到图5。图5（d）和（e）波形基本一致。这是因为虽然不满足E4≪E1，但是由于此时带通滤波器输出只包含E1，此时带通滤波器提取的电压波动信号与E1，即与调幅波信号一致。

（3）fi＝80Hz时被测电压信号为

式中ui＝0.1，fi＝80Hz，fc＝50Hz。

被测电压波形，自乘求平方后波形，通过0.05～35Hz带通滤波器后波形如图6所示。图6（c）是0.05～35Hz带通滤波器输出波形。图6（d）截取了图6（c）中t＝0.75～1.25s时段的波形，图6（e）是相位补偿后调幅波波形。从图6（d）和（e）可以看出，通过0.05～35Hz带通滤波器提取的电压波动信号幅值约为0.05，与调幅波信号幅值不一致，其幅值约为调幅波信号的一半，而且波动频率不等于调幅波信号的频率，而是等于2fc－fi＝20Hz。实验结果符合本文式（9）的结论：因为fi∈（67.5 99.95）Hz范围，所以带通滤波器输出主要包含E2。由式（3）可知E2的幅值是E1幅值的一半，所以带通滤波器提取的电压波动信号是调幅波幅值E1的一半。

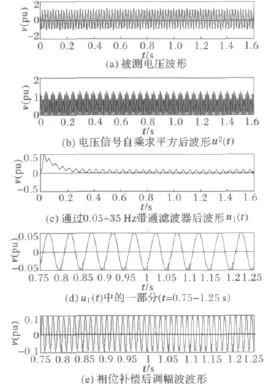
图6 调幅波频率为80Hz的试验波形Fig.6 Test waveforms with a modulation frequency of 80Hz

（4）fi＝120Hz时被测电压信号为

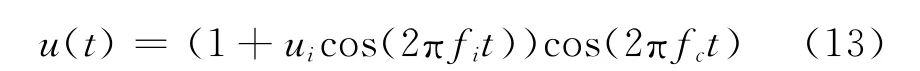
式中ui＝0.1，fi＝120Hz，fc＝50Hz。

被测电压波形，自乘求平方后波形，通过0.05～35Hz带通滤波器后波形如图7所示。图7（c）是0.05～35Hz带通滤波器输出波形。图7（d）截取了图7（c）中t＝0.75～1.25s时段的波形，图7（e）是相位补偿后调幅波波形。从图7（d）中可以观察通过0.05～35Hz带通滤波器提取的电压波动信号的幅值约为0.05，与调幅波信号幅值不一致，其幅值约为调幅波信号的一半，而波动频率不等于调幅波信号的频率，而是等于fi－2fc＝20 Hz。与本文式（9）的结论一致。

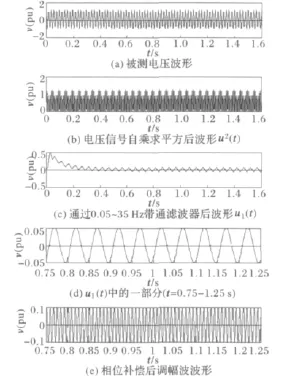
图7 调幅波频率为120Hz的试验波形Fig.7 Test waveforms with a modulation frequency of 120Hz

4 结论

本文在IEC给出的闪变仪设计原理的基础上，研究了周期性闪变调制信号模型的频率特性。得出结论：

1）当调幅波频率fi在（0.05，35）Hz，（65～99.95）Hz和（100.05～135）Hz范围内时均有可能产生明显闪变。

2）影响闪变的电压波动分量不一定等于调幅波分量；只有当调幅波频率在17.5～35Hz范围内时，影响闪变的电压波动分量才等于调幅波的分量。

3）当调幅波频率fi在（65～99.95）Hz和（100.05～135）Hz范围内时，影响闪变的电压波动频率主要为｜2fc－fi｜，波动幅值约为调幅波幅值的一半。

4）如 果 ui值 比 较 大，当 fi∈ （0.05 17.5）Hz，闪变主要受E1和E4分量影响，而不是只受E1影响。如果只把调幅波信号E1看作是影响闪变的电压波动信号，就会产生较大的误差。

［1］ 肖湘宁.电能质量分析与控制［M］.北京：中国电力出版社，2004.

［2］ 贾秀芳，赵成勇，胥国毅，等 （Jia Xiufang，Zhao Chengyong，Xu Guoyi，et al）.IEC闪变仪误差分析及改进设计（Error analyzing of IEC flickermeter and its improving design）［J］.电工技术学报（Transactions of China Electrotechnical Society，），2006，21（11）：121－126.

［3］ Heydt G T，Bakroun M，Inan A.Voltage flicker estimation based on linearization and Lp norms［J］.IEEE Trans on Power Delivery ，2003，18（4）：1564－1566.

［4］ Srinivasan Krishnaswamy.Digital measurement of voltage flicker［J］.IEEE Trans on Power Delivery，1991，6（4）：1593－1598.

［5］ Girgis Adly A，Makram Elham B.Measurement of voltage flicker magnitude and frequency using a Kalman filtering based approach［C］∥Canadian Conference on Electrical and Computer Engineering，Calgary，Canada：1996.

［6］ Huang Shyhjier，Lu Chenwen.Enhancement of digital equivalent voltage flicker measurement via continuous wavelet transform［J］.IEEE Trans on Power Delivery，2004，19（2）：663－670.

［7］ Soliman S A，El－Hawary M E.Measurement of power system voltage and flicker levels for power quality analysis：a static LAV state estimation based algorithm ［J］.International Journal of Electrical Power and Energy System，2000，22（6）：447－450.

［8］ Chen M T.Digital algorithms for measurement of voltage flicker［J］.IEE Proceedings：Generation，Transmission and Distribution，1997，144（2）：175－180.

［9］ 王 志 群，朱 守 真，周 双 喜 （Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi）.Hilbert变换求取电压闪变有关参数（Parameter estimation of voltage flicker through Hilbert transform）［J］.电力系统自动 化 （Automation of Electric Power Systems），2004，28（5）：34－37，66.

［10］马玉龙，刘连光，张建华，等（Ma Yulong，Liu Lianguang，Zhang Jianhua，et al）.IEC闪变测量原理的数字化实现方法（Research of digital flickermeter based on IEC standard）［J］.中国电机工程学报（Proceedings of the CSEE），2001，21（11）：92－95.

［11］ 余丹，李群湛，唐伟，等（Yu Dan，Li Qunzhan，Tang Wei，et al）.电压闪变仪的软件设计及其应用（Software design of voltage flickermeter and its practical application）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2006，18（3）：64－67.