多脉波整流技术在风力发电中的应用

陈 杰 龚春英 陈家伟 张方华 严仰光

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

变速风力发电机组因为具有风能利用效率高、机组的动态载荷小等突出的优势，成为了当前风电市场上的主流机型[1-3]。全功率型机组，如永磁直驱和半直驱机组，变速运行范围广、风能利用效率高、零电压穿越能力强、对电力系统的负面影响小，是今后的一个主要发展方向，也是当前国内外研究的热点和重点[4-6]。对于变速机组，为了实现机组转速和电网频率的解耦，需要在机组和电网之间增加功率变换器。

目前，风电机组中常用的整流器有二极管不控整流和背靠背的电压型PWM整流两种结构。前者存在发电机的输出电流谐波含量大、功率因数低、机组的转矩脉动大等缺点，多用于中小功率场合；而后者虽然发电机的输出功率因数较高，但数量众多的功率开关器件不仅增加了成本，还大大地降低了系统的可靠性。文献[7]对当前主流变速机组各部件的故障发生率和因故障导致机组停机的时间进行了研究，结果显示因变流装置等电气设备故障造成的停机时间竟高达 32.5%。可见，提高变流装置的可靠性是改善风力发电机组的可靠性、减小维护成本的关键。另一方面，我国风电领域的功率变流器仍主要依赖进口，变流器的国产化程度低。因此，研究和发展新型的功率变换器是我国风力发电面临的一个重要课题。

多脉波整流器具有结构简单、可靠性高及功率因数高等突出优点，在大功率整流和航空航天领域得到了广泛的应用[8-11]。但是，将其用于风力发电场合却鲜有报道，文献[8]提出了将一种 12脉波自耦变压整流器（Autotransformer Rectifier Unit，ATRU）应用到直驱型风电系统中，但是文章的重点实质上仍然是对多脉波整流电路本身的研究，未涉及风电相关技术。

本文在介绍一种新型 12脉波 ATRU的工作原理和风电机组的基本特性的基础上，进一步分析了将多脉波整流技术应用到风力发电这一特殊场合的可行性，说明了在该场合下自耦变压器容量的设计要求。研制了一套实验样机，验证文中理论分析的正确性和ATRU在风电场合应用的可行性。

2 三相桥式不控整流

对于中小功率风力发电系统，通常采用图1所示的系统结构。由风力机、永磁同步发电机（PMSG）、升压斩波电路以及电压源型并网逆变器组成。由于采用不控整流电路，发电机的输出相电流波形呈脉冲状，含有大量的低次谐波，使得发电机的转矩脉动比采用PWM整流时要大很多，容易引起机组的机械结构谐振和疲劳损坏。另外，由于发电机的功率容量有限，输出电流的畸变引起了输出电压的畸变，使得发电机的输出电压也含有大量的低次谐波。图2a给出了采用不可控整流时PMSG输出电压和电流波形，很明显，此时PMSG的输出电压波形已经接近方波。图2b和图2c分别给出了PMSG输出电流和电压波形的傅里叶分析（FFT）结果，可以看出电压和电流波形中均含有大量的低次谐波。另一方面，考虑到当前用于风电场合的PWM整流器结构复杂、成本高和存在故障率高的问题，故本文最终将研究目标锁定于多脉波整流技术。

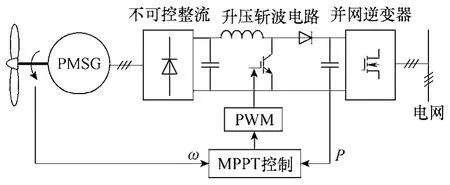
图1 传统不控整流风力发电系统Fig.1 Conventional wind power generation system with diode rectification

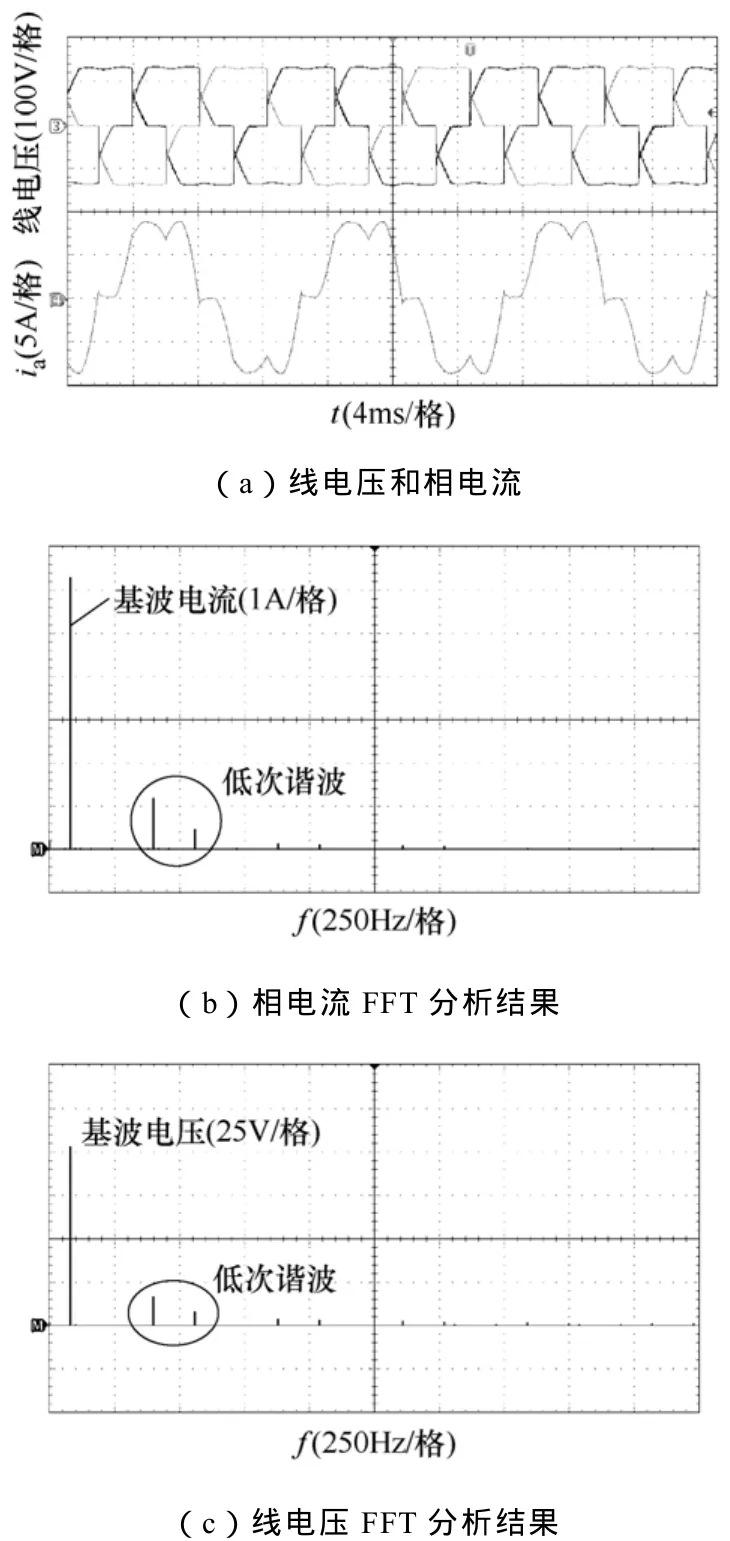
图2 PMSG经不控整流输出电压和电流波形Fig.2 Output voltage and current waveforms of PMSG with diode rectification

3 12脉波ATRU原理及特性分析

3.1 工作原理

图3所示为新型12脉冲自耦变压整流器的结构框图，图中Lsa、Lsb、Lsc为输入电感，用来抑制输入电流突变，提高输入电流的正弦度。自耦变压器绕组采用多边形联结，各绕组同名端如图3所示。图4给出了自耦变压器的磁路图，每个铁心柱有三个绕组。对于左边的铁心柱，长绕组a′b″和短绕组c′c、cc″同向绕制，短绕组 c′c、cc″分别用于滞后、超前移相。通过绕组移相，由输入三相电压va、vb、vc产生的两组幅值相同但相位分别超前与滞后输入电压 15°的三相电压 va′、vb′、vc′和 va″、vb″、vc″，从而得到两组相位相差30°的三相电压。这两组三相电压分别经不控整流后通过平衡电抗器并联连接到负载。

图3 新型12脉冲自耦变压整流器Fig.3 Novel 12-pulse ATRU

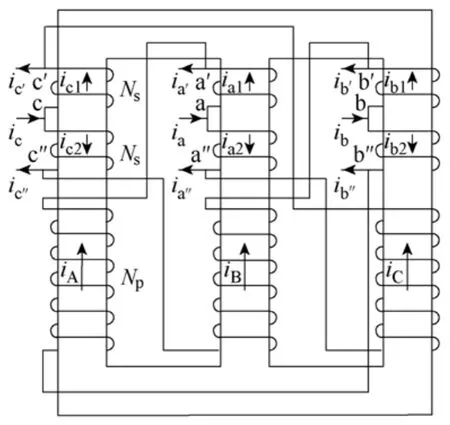
图4 自耦变压器磁路图Fig.4 Magnetic circuit of auto-transformer

图5给出了自耦变压器电压矢量图。下面将结合图3和图4，简要分析一下移相的原理和图5的由来。以中柱为例，长绕组 b′c″、短绕组 a′a、aa″以相同方向绕制在同一个铁心柱，故三个绕组的电压相位相同。用矢量表示就是 Vc″b′与 Va′a和 Vaa″方向相同（平行），而矢量长度与长短绕组的匝比有关。对于三相对称输入，每个铁心柱上的矢量以 120°均匀分布。根据图3中自耦变压器的联结方式可知，图5中的VbVcVc″Vb′四点构成一个等腰梯形，故线电压Vcb平行于 Vc″b′，且与相电压 Va垂直。因此，可以知道相电压 Va与 Va′a和 Vaa″也互相垂直，从而形成了 Va′超前 Va一定相位，Va″滞后 Va一定相位的结构。而且，只要改变短绕组与长绕组的匝比就可以改变自耦变压器产生的两组相电压Va′与Va″的相位差。

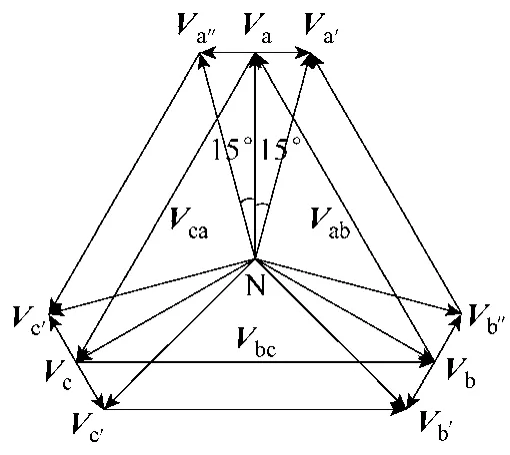
图5 自耦变压器电压矢量图Fig.5 Voltage vector diagram of autotransformer

根据设计要求，输入三相电压产生的两组三相电压分别超前与滞后于输入三相电压15°，定义输入三相相电压va与超前三相相电压va′的有效值分别为Vin、Vs，根据电压矢量图有

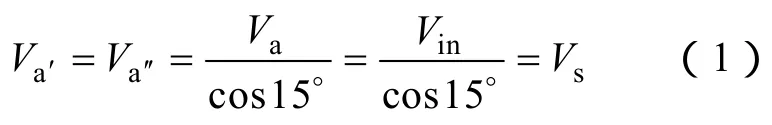
由式（1）可以看出，自耦变压器移相产生的三相电压幅值略大于输入三相电压幅值。

定义长绕组与短绕组的匝数分别为Np、Ns，两端的电压有效值分别为VNp、VNs。根据电压矢量图可得

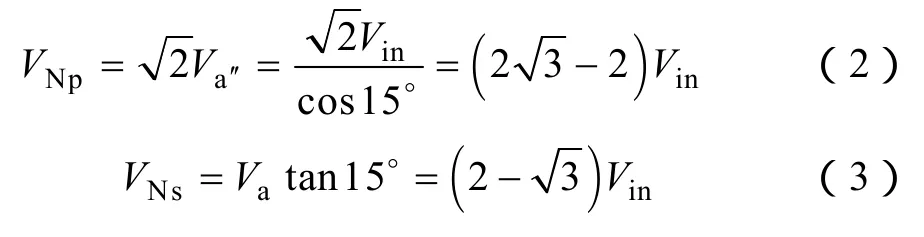
由式（2）、式（3）可得长绕组与短绕组的匝比为

只要长绕组与短绕组的匝比满足式（4），便可以由自耦变压器产生两组相位相差 30°的三相电压，满足12脉冲整流的要求。

3.2 输出电压分析

根据图3，整流桥经平衡电抗器并联输出到负载，整个整流器可以看作是上下两个三相双半波不控整流电路的串联。由于引入了平衡电抗器，二极管的导通角由60°增大到120°，流过二极管的电流由无电抗器时的Id减小为Id/2，其中Id为负载电流。整流器的输出电压可以表示为

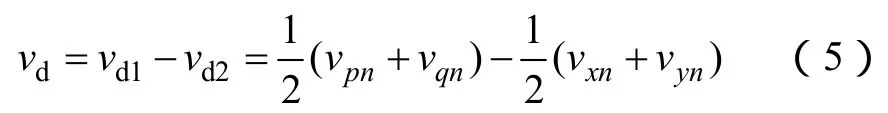
结合图 4，可以得到整流器 vd1、vd2、vd各点的理想电压波形如图 6中的粗实线所示。故而可得整流器输出直流电压平均值为

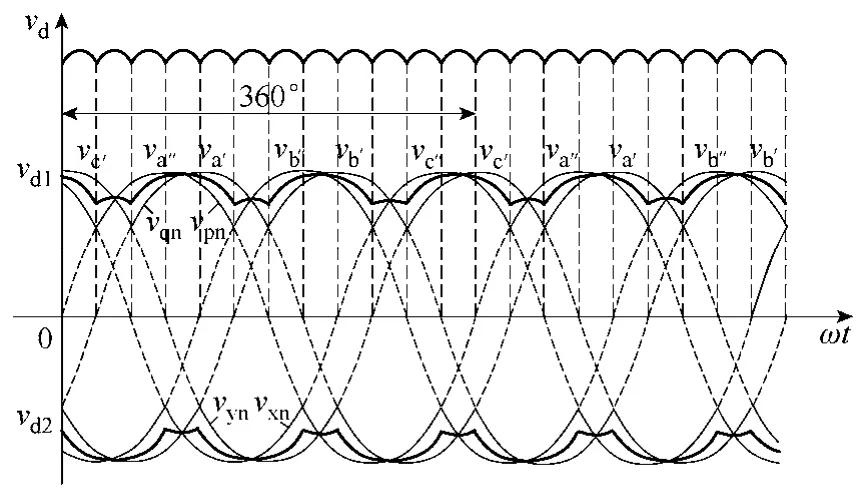
图6 整流器输出电压波形图Fig.6 Output waveforms of ATRU

式中，Vl为输入线电压有效值。

3.3 输入电流分析

由于ATRU输出电压不可控，风力发电系统的并网逆变可以有两种实现方式：①输出直接接电流源型并网逆变器；②通过 Boost升压电路抬升稳压后接电压源型并网逆变器。无论是 Boost升压电路还是电流源型逆变器，其输入侧都存在一个大电感，故可近似认为ATRU输出电流是时刻连续的。另外，平衡电抗器保证了两组整流桥独立工作，互不影响，各分担一半的负载电流，只是在相位上相差30°。

结合图4，对于每个铁心柱，根据磁势平衡原理可得

对结点 a、a′、a″，根据基尔霍夫电流定律，可以得到

相同的，对于节点 b、b′、b″、c、c′、c″，可以得到与式（8）完全类似的关系式，仅下标不同。再联合式（7）、式（8），可得

根据式（7）～式（9）和图3、图4可得自耦变压器各绕组的电流波形和a相电流波形如图7所示。其中，a相电流可表示为

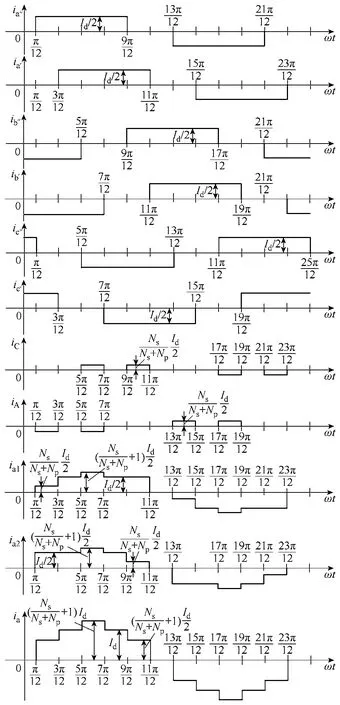
图7 新型12脉冲ATRU输出电流波形Fig.7 Output current waveforms of ATRU

将输入电流ia正、负波形的中点作为时间零点对其进行Fourier级数分解得

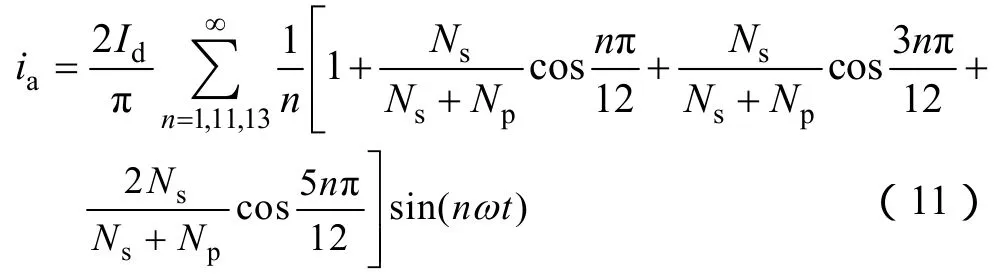
从式（11）可以看出，整流器输入电流含 12k±1次谐波，最低次谐波为11次谐波。输入基波电流有效值为

所以输入电流总谐波畸变（Totall Harmonic Dstortion, THD）[12]约为

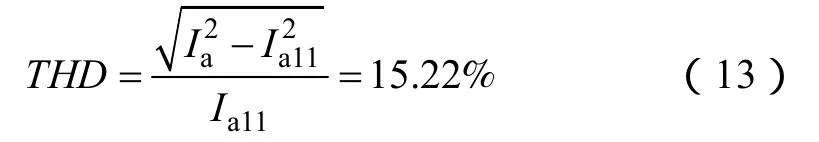
式中，Ia为a相总电流有效值，可由图7最后一个波形计算得到。

实际电路中由于线路阻抗的存在，THD会更小。根据图7中变压器各绕组的电流波形，可以得到长绕组和短绕组的有效值分别为

最终，可以得到变压器的等效容量为所有绕组伏安之和的1/2，即

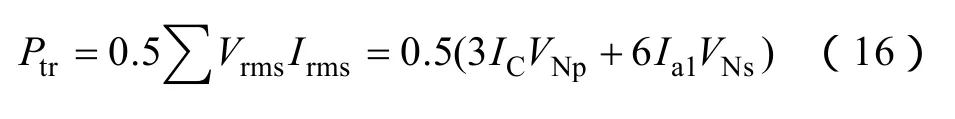
联合式（2）、式（3）、式（6）、式（14）～式（16）可以求出变压器的总容量为0.182VdId。可以看出，文中提出的 12脉冲 ATRU所用的自耦变压器等效容量仅约为输出功率的 18%，与传统的 12脉冲变压整流器相比，变压器容量减小了82%，可以避免变压整流器体积庞大的缺点。

4 ATRU与风电机组的关系

变速风力发电机组的转速随着风速的变化而变化，从而造成发电机的输出电压和功率的变化范围很宽，此处将对风电机组与ATRU的关系进行深入的分析，得出ATRU在风电场合的设计标准。

风力机的机械功率为

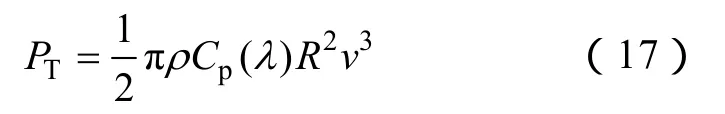
式中，PT为风力机的气动功率；ρ 为空气密度，通常取为1.225kg/m3；R为风轮的半径；v代表风速。Cp(λ)为风能利用系数，是叶片速比λ 的函数，且

式中，ω 为风力机的转速。

为简化分析，认为风电机组仅有两种运行工况，即额定风速以下的最大功率跟踪运行和额定风速以上的恒功率运行。且机组在额定风速以上的功率限制由桨距角的调节来实现，转速保持不变。那么，根据两种运行工况可以写出风力机气动功率关于风速的函数

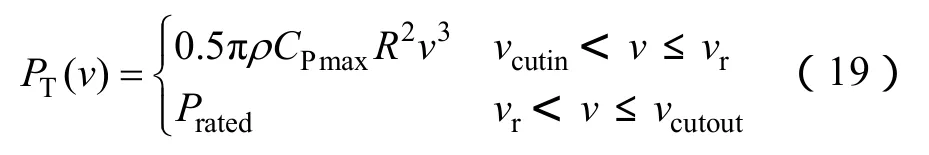
式中，vr定义为额定风速；vcutin表示切入风速；vcutout表示切出风速。

在额定风速以下，机组以恒定的叶尖速比 λopt即MPPT运行，将式（18）代入式（19），可得

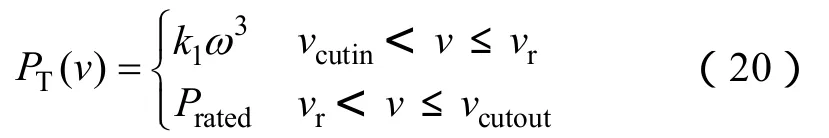
其中

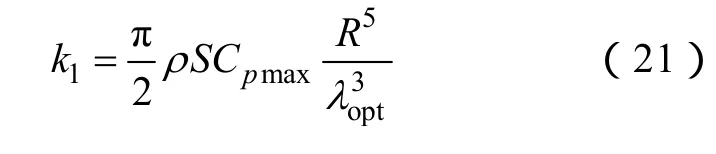
对于给定的一台风力发电机组，式中k1为一个常数。换言之，在额定风速以下，当机组运行于最大功率跟踪控制时，机组的气动功率是转速ω 的 3次函数。

自耦变压器的设计通常可以由SQ值来确定[13]

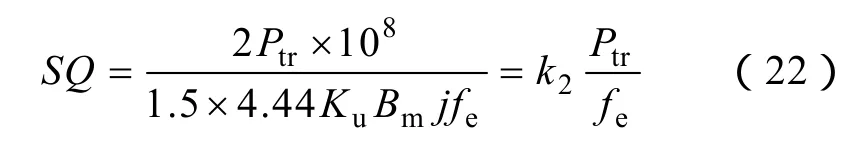
式中，SQ为铁心有效截面积和窗口面积的乘积，其中 S为磁心有效截面积，Q为窗口面积；k2=（3.33KuBmj×10-8）-1；Ku为窗口填充系数；Bm为最大工作磁密；j为电流密度；fe为电角频率。

从式（22）中可以看出，SQ值不仅与功率有关，还与fe有关，其大小取决于功率与频率的比值。

假设发电机的极对数等于p，则式（22）可表示为

可见，SQ值是风电机组运行转速的2次函数，峰值出现在机组的额定功率（即额定转速）处，而风机的气动功率是转速的3次函数。因此，只要在额定功率点对变压器进行设计，就可以保证在额定功率以下不会出现铁心饱和的现象。

为简化分析，进一步假设发电机为隐极式永磁同步发电机，不计磁饱和，忽略电枢绕组电阻和温度变化对永磁体磁通的影响，那么定子绕组感应的励磁电动势可以近似的表示为[13]

式中，N1为定子绕组匝数；kw1为基波绕组因数；Φ0表示气隙主磁通；k为齿轮箱的增速比。

代入（6）式可以得到ATRU的输出电压

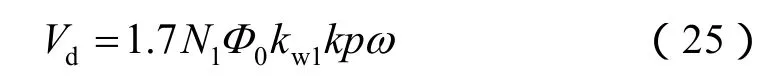
在额定功率点处，结合式（24），可以得到变压器绕组的匝数计算公式[13]

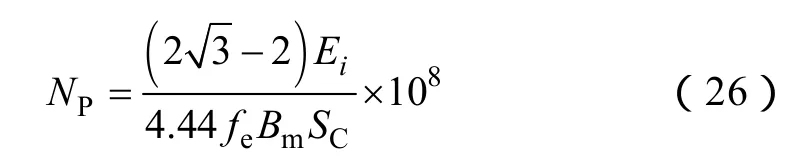
式中，SC为根据SQ值选取的铁心的有效截面积。

由以上分析可以得到如下结论：

（1）与航空变频电源场合不同，风力发电的输出功率是转速的3次函数，只要自耦变压器的设计点选取在额定功率处就可以保证铁心不会出现饱和现象。

（2）在功率等级相同的情况下，电机的转速和极对数对自耦变压器的尺寸起决定性作用。为减小自耦变压器体积，在设计风力发电机的时候，可考虑适当地提高发电机转速和极对数。

（3）给出了发电机绕组匝数与整流后直流电压的关系。也就是说，由后级并网变换器对母线电压的要求和风机的转速范围可以求出发电机的设计要求。

5 实验分析

5.1 实验平台介绍

为了验证理论分析的正确性和在风电场合的可行性。开发了一套风力发电模拟平台，有两台10kW背靠背的永磁同步发电机，其中一台用来模拟风力机，一台作为发电机。ATRU的额定功率为2kW，自耦变压器长、短绕组的匝数分别为 285匝和 52匝。

5.2 仿真及实验结果分析

图8a给出了功率为1kW时ATRU的输入线电压和a相电流波形。与理论分析的输入电流波形相比，实际电路中由于使用了输入滤波电感，即图 3中 Lsa、Lsb、Lsc，输入电流的波形变得更加平滑，正弦度更好。图8b给出了PMSG输出相电流（即ATRU输入相电流）波形的傅里叶分析结果，图中除了11和13次谐波以外，基本上看不到其他谐波的存在。与理论分析完全一致。而输入电压则由于受电流的影响，也变成阶梯波形状，对应的也存在11和13次谐波，其傅里叶分析结果见图8c。

图8 基于ATRU的风力发电系统实验结果Fig.8 Experimental results of wind power generation system based on ATRU

图8d给出了输出功率等于1kW时ATRU的输入电压和输出电压波形。用于风力发电场合时其输出电压纹波在5V左右，约为输出电压的4%。与输入电源为电网时不同，由于风力发电机的功率容量不可能无穷大，PMSG的输出电压（即ATRU的输入电压）的波顶部分别削除。因此，在风电场合ATRU的最终输出电压纹波要比其他场合小很多。

图9给出了采用不控整流和ATRU整流两种情况下PMSG的输出电压和电流的实测THD值。可以看出，采用ATRU可以有效的降低输入电流和电压波形的THD。

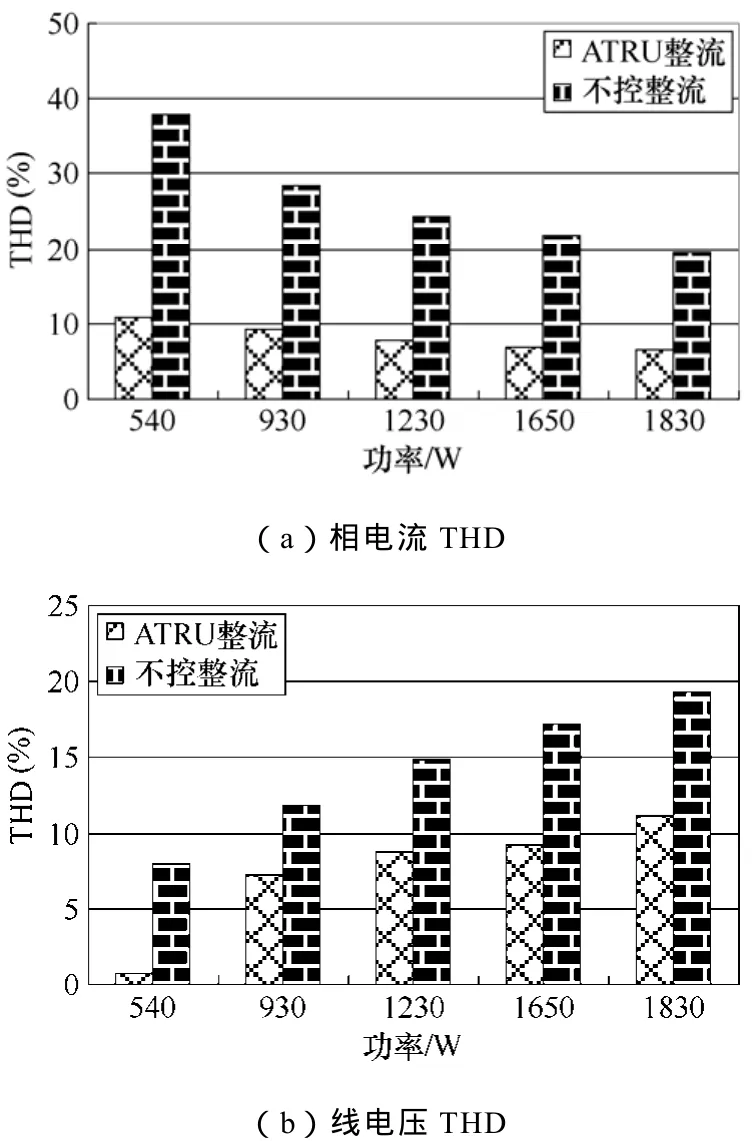
图9 不控整流与ATRU输入电压和电流的THD比较Fig.9 Comparative study of input voltage and current THD of diode rectifier and ATRU

6 结论

（1）本文对一种新型 12脉波自耦变压整流器的工作原理、输入电流和输出电压特性进行了分析，指出多脉波整流技术可以提高风力发电机的输出功率因数和有功输出能力，减小电流谐波含量，降低发电机损耗，抑制转矩脉动。

（2）讨论了ATRU与风电系统之间的关系，及其设计要求，指出风电系统的转速和功率的大范围变化对ATRU自耦变压器的设计影响较小，只要在合理的工作点下对其进行设时，就能够满足全范围运行的要求。

[1]Li H, Chen Z. Overview of different wind generator systems and their comparisons [J]. IET Renewable Power Generation, 2007, 2(2): 123-138.

[2]Slootweg J G, Vries E de. Inside wind turbines—fixed vs. variable speed [J]. Renew Energy World, 2003,6(1): 30-40.

[3]Chinchilla Mónica, Arnaltes Santiago, Burgos Caros.Control of permanent-magnet generators applied to variable-speed wind-energy systems connected to grid[J]. IEEE Transactions on Energy Conversion, 2006,21(1): 130-135.

[4]Polinder Henk, Frank F A, Van Der Pijl, et al.Comparison of direct-dirve and geared generator concepts for wind turbines [J]. IEEE Transactions on Energy Conversion, 2006, 21(3): 725-733.

[5]尹明, 李庚银, 张建成, 等. 直驱式永磁同步风力发电机组建模及其控制策略[J]. 电网技术, 2007, 31(15): 61-65.Yin ming, Li Gengyin, Zhang Jiancheng, et al.Modeling and control strategies of directly driven wind turbine with permanent magnet synchronous generator[J]. Power System Technology, 2007, 31(15): 61-65.

[6]姚骏, 廖勇, 庄凯. 永磁直驱风电机组的双PWM变换器协调控制策略[J]. 电力系统自动化, 2008,32(20): 88-92, 107.Yao Jun, Liao Yong, Zhuang Kai. Coordinated control strategy of back-to-back PWM converter for permanent magnet direct-driven wind turbine[J].Automation of Electric Power Systems, 2008, 32(20):88-92, 107.

[7]Ribrant J, Bertling L M. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005 [J]. IEEE Transactions on Energy Conversion, 2007, 22(1): 167-173.

[8]温春雪，李建林，许洪华. 多脉波整流电路在直驱式风力发电中的应用[J]. 电力电子技术, 2008,42(5): 59-60.Wen Chunxue, Li Jianlin, Xu Honghua. Research on multi-pulse rectifier suitable for direct-drived wind power system[J]. Power Electronics, 2008, 42(5):59-60.

[9]Wu B, Li Y, Wei S. Multipulse diode rectifiers for high-power multilevel inverter fed drives [C].Proceedings of the 9th International Power Electronics Congress, 2004, 1: 17-22.

[10]Sun Jian, Bing Zhonghui, Karimi K J. Small-signal modeling of multipulse rectifiers for more-electric aircraft applications[C]. Proceedings of the IEEE Power Electronics Specialist Conference, 2008, 1:17-22.

[11]Bhim Singh, Sanjay Gairola, Briij N. Singh, et al.Multipulse AC-DC converters for improving power quality: a review[J]. IEEE Transactions on Power Electronics, 2008, 23(1): 260-281.

[12]陈坚. 电力电子学[M]. 北京: 高等教育出版社, 2002.

[13]Colonel Wm T McLyman. Transformer and Inductor Design Handbook, 3rd ed(Electrical and Computer Engineering)[M]. New York, Marcel Dekker Press,2004.