通道不一致性对自适应调零天线的影响分析✴
何凌云
(中国西南电子技术研究所,成都610036)
通道不一致性对自适应调零天线的影响分析✴
何凌云
(中国西南电子技术研究所,成都610036)
为了提高自适应调零天线的抗干扰性能,分析了通道不一致性对自适应抗干扰LMS(最小均方)算法稳定性、收敛时间等方面的影响。同时仿真和分析了系统中造成通道不一致性的因素,仿真结果证明幅、相差异会严重恶化系统的性能。最后,给出了工程应用中的相应解决措施和设计指导原则。
自适应调零天线;抗干扰;通道不一致性;LMS算法
1 引言
自适应调零天线是一种根据外部干扰环境的变化,自动调整天线方向图,使方向图零点对准干扰方向,从而保证系统最佳工作状态的天线。随着目前电子对抗的日渐激烈以及自适应抗干扰天线理论研究的逐渐深入,自适应调零天线已经开始走向工程实用化。
自适应调零算法作为自适应阵列处理的核心,已经能够在大量的文献中查找到相关的资料[1-5],各种算法的软件仿真和理论分析已经比较成熟。但是在工程化的过程中,由于硬件实现中带来的阵元互耦、信道幅相差异、ADC采样误差等因素,会造成调零算法收敛缓慢或不收敛、形成调零零陷变宽变浅、方向图利用率降低等后果。
本文详细分析了各种因素对自适应调零天线中抗干扰算法性能的影响,通过Ansoft HFSS和Matlab对其进行了仿真验证,并进一步给出了相应的解决措施和设计原则,对具体的工程应用具有一定的理论和实际价值。
2 自适应调零算法
自适应调零天线利用扩频系统伪随机码信号深埋在热噪声中的特点,使进入接收机系统的总输入功率减至最低限度,可以有效地促使强干扰源电平降低到热噪声水平[1-2]。天线接收到的信号经前端放大、A/D转换、LMS算法处理后,用得到的每路加权值去控制权值调整网络,经幅相调整后的信号合成一路输出,从而在天线阵的方向图中产生对着干扰源方向的零点,以增加抗干扰的效能。
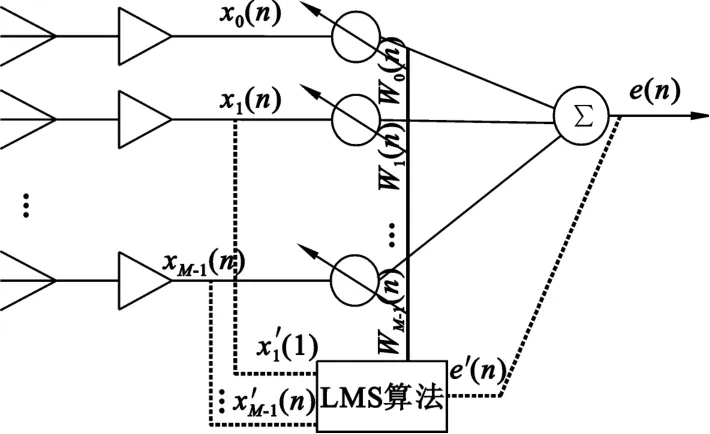
图1 自适应调零系统组成原理图Fig.1 Schematic diagram of adaptive nulling system
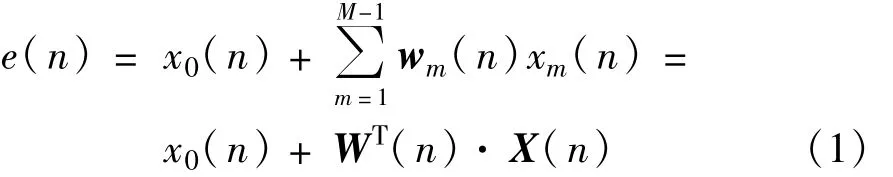
根据最小均方误差准则[3,5],最佳的滤波器参数wopt应该使性能函数均方误差
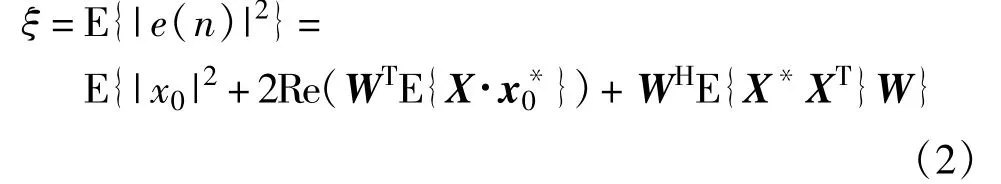
为最小。均方根误差性能函数ξ为w的二次函数,它符合二次函数的特点,仅存在唯一最佳的极小点。由它对w的梯度为0,即可求出其最小值的必要条件。
使ξ取最小值的w的最佳值wopt应满足方程
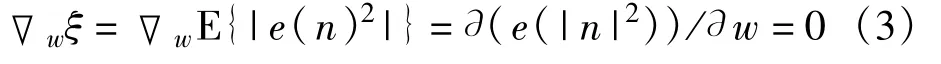
沿着ξ减少的方向调整w,可以找到wopt。这样自然会采用如下最陡下降的递推公式来调整w以寻求wopt:
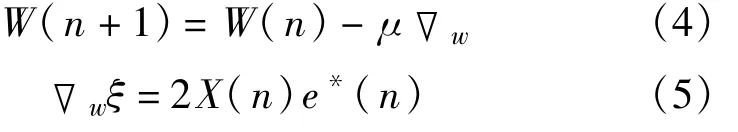
式中,▽wξ为ξ的梯度,其中μ为一个用于控制自适应算法速度和稳定度的常数,称为步长因子。通过一系列的运算,可以得到以下递推公式:
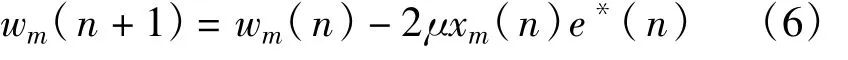
对于图1,[x1(n),x2(n),…,xm-1(n)]表示天线接收到的阵列信号,[w0(n),w1(n),…,wm-1(n)]表示阵列权值矢量。每个天线阵元接收到的信号与权值相乘后再求和,作为阵列的输出信号e(n)。
为了避免得到无意义的解w(n)=[0,0,…,0],一般固定w0(n)=1(主通道),各辅助通道对应的权值调整矢量为wm(n)(n=1,2,…,N-1)。阵列合成输出信号e(n)为
因此,式子中几个参数的精确与否直接影响到计算的结果,以及整个调零天线的性能。从图1中可以看出,ADC采样后输入给算法处理的信号,与理论分析时所认定的信号有很大差异,实际计算时式(6)应该为
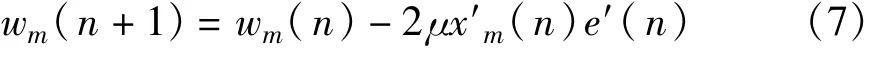
式中,x′m(n)=amxm(n)e-jφm,e′(n)=be(n)ejψ,am、b以及φm、ψ分别为实际采样信号和理论信号的幅、相误差,它不仅包含有源信道中幅相差异,还包含了各天线阵元、通道互耦、一致性、采样误差等众多因素的影响。式(7)可以近似变成
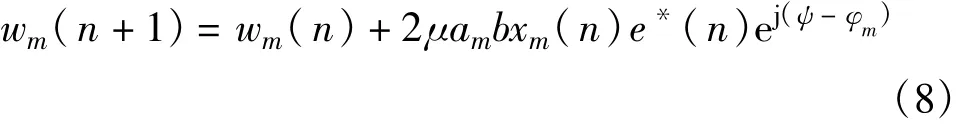
采样信号的幅度差am、b造成算法稳定因子μ发生变化,μamb会对算法的收敛时间和稳定性造成影响。在极端情况下可以简单的理解为:当幅度过大时,将超过AD器件动态,导致器件采样饱和,算法无法正常运算,最终不能收敛;当幅度过小时,采样得到的弱干扰信号将无法与系统白噪声区分开,将严重影响天线的抗干扰能力,恶化调零天线的SINR。
相位误差因子ej(ψ-φm)与算法的最陡收敛梯度矢量相乘,将影响到算法的迭代方向。如果|ψ-φm|<90°,表示算法的迭代方向与最陡收敛梯度矢量方向一致,虽然收敛时间会增加,但最终算法还是会处于收敛状态;如果|ψ-φm|=90°,表示算法的迭代方向与最陡收敛梯度矢量方向垂直,此时算法失效,天线的输出功率不变;如果|ψ-φm|>90°,表示算法的迭代方向与最陡收敛梯度矢量方向相反,这种情况下算法处于发散状态,天线的输出功率会越来越大,直到达到所有通道同相合成的最大功率值。
3 算法影响因素分析
自适应调零天线的硬件部分主要由4部分组成:天线阵面、连接电缆、有源模拟信道、数字处理。公式(8)中的幅相误差因子的因素主要包括:天线单元的增益一致性;天线单元之间、模拟信道之间及数字信号之间的互耦[4];连接电缆的幅相差;模拟信道、数字板各通道的幅相差以及AD采样误差等。以上因素有些可以通过改进设计解决(比如电缆幅相、模拟信道互耦、数字信号隔离、AD采样误差),有些不能或不能完全解决,需要在设计时采取措施降低影响或增加补偿。下面对后者进行详细分析。
3.1 天线阵面
天线阵面包括阵元互耦和增益一致性两方面。考虑到阵元互耦,设矩阵C为互耦矩阵,它是一个N×N的复矩阵,可以将其表示为
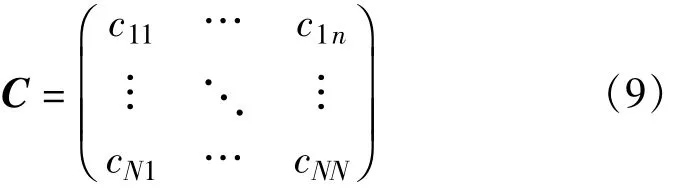
式中,cmn(m≠n)表示第n个阵元对第m个阵元的互耦,cmm表示第m个阵元的自耦。理想情况下当阵元的互耦无限小时,互耦矩阵可以看成为一个对角矩阵。考虑到互耦时阵列接收信号X(n)应该为CX(n)。
天线增益的不一致性主要发生在低仰角时。我们从自适应调零天线的使用情况来看,这一新技术首先应用在弹、机载平台,而干扰信号的来源有两个方面:一是地面固定站、车载、手持式干扰源;二是专用干扰飞机。因此可以看出干扰源和调零天线的位置关系,以调零天线为坐标,天顶为俯仰90°,则干扰源多处于方位0°~360°、俯仰-10°~+30°的位置,即干扰源多在调零天线的低仰角方向。受平台尺寸和天线互耦的影响,天线方向图在低仰角的不圆度很差,以4阵元方形阵列调零天线为例,从图2得出4个天线阵元在水平面的最大增益差超过10 dB,若考虑到极化一致性,增益差还将变大。
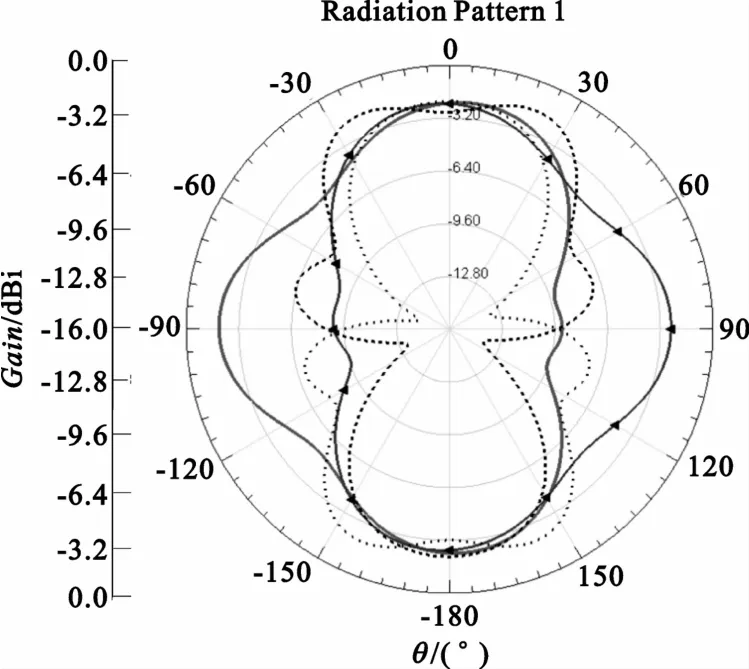
图2 天线水平面不圆度Fig.2 Un-roundness in horizontal direction
3.2 有源信道
信道是自适应调零天线中最关键的硬件部分,由放大、滤波、功分、混频、矢量调制、合成等器件组成。可以通过器件排布、腔体隔离、电源滤波等方式提高各路之间隔离度,并减小各路之间的幅相差,各通道间很容易做到幅度差±1 dB、相位差±5°。信道的影响主要来自于xm(n)和e(n)之间的幅相差(如图1),幅度差异可以控制,但相位差异无法解决,应选取合适的器件,并缩短信号路径,使|ψ-φm|尽可能地小。
4 仿真分析及解决措施
我们以图3中方形的4元自适应调零天线为例,通过仿真来分析幅相误差对天线算法及抗干扰调零效果的影响,同时提出了改进的设计方法。

图3 自适应调零天线阵面Fig.3 Plane array of adaptive nulling antenna
4.1 各通道的幅度差异仿真
在公式(8)中,由于|wm|≤1,为了使收敛功率无限逼近零,则首先必须满足am≥1,即辅助通道接收到信道的功率必须大于主通道。若+a23≥1,则天线至少能对抗一个干扰信号;若满足每个am均大于1,则天线阵可以同时对抗3个干扰信号。
设定干扰源的方向为方位90°、俯仰0°,此时从图2可以看出,由于4个天线阵元在水平面的不圆度很差,造成各路通道之间的幅度差很大。如果我们按照图2中各天线在该方向的增益差来改变4路接收通道之间的幅度(1,0.4,0.35,0.35),则0.42+ 0.352+0.352=0.405<1。此时3路辅助通道的功率和小于主通道的功率,算法无法收敛,抗干扰功能失效,需要对辅助通道的增益进行调整。
若要满足a21+a22+a23≥1,则必须选用增益低的通道作为主通道,我们设定4路通道的幅度分别(1,1,2,0.9),观察收敛后的阵列方向图和收敛功率的变化,图4和图5中(a)、(b)分别为理想收敛情况(通道的幅度为(1,1,1,1))和现状态下(通道的幅度为(1,1,2,0.9))收敛情况(合成方向图增益用极坐标等高线投影的方式表示)。
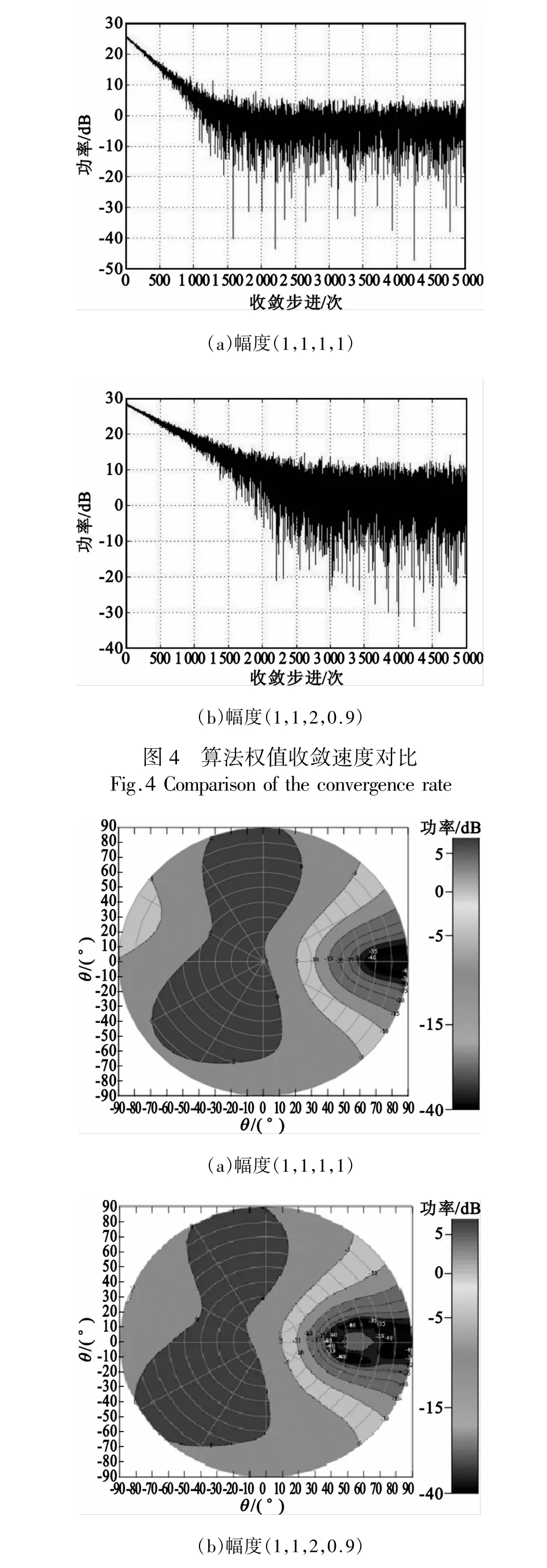
图5 收敛后阵列方向图对比Fig.5 Comparison of the patterns in array antennas
从图可以看出,通道幅度不一致性不仅会导致调零算法收敛速度下降,而且收敛后的阵列合成方向图中,天线零陷会变浅变宽,低增益所占的空域变大,即合成方向图的空间利用率降低。
4.2 各通道的相位差异仿真
相位差异分两种,一种是各辅助通道和主通道之间的相位差,一种是某个辅助通道与合成通道之间的相位差。前者的相位变化可以等效成阵列空间干扰信号不同入射方向的情况,这种情况在算法收敛时权值会自动补偿这个相位差,不会影响到算法收敛速度和合成方向图;后者则可以等效于|ψ-φm|的情况,|ψ-φm|=0°和0°<|ψ-φm|<90°的收敛情况和合成方向图类似于图4和图5;|ψ -φm|=90°和|ψ-φm|>90°时的收敛结果分别如图6(a)和图6(b)所示。
从图6可以看出:当|ψ-φm|=90°时,计算权值基本维持不变;当|ψ-φm|>90°时,权值会按照4路通道的最大合成功率收敛,最终稳定在最大合成功率输出,两种情况都会导致算法失效。
4.3 解决措施
通过上述仿真分析可以看到,通道的幅相不一致性不仅会降低算法的稳健性和收敛速度,而且还会恶化天线阵列的合成方向图,极大地影响自适应抗干扰的性能。在工程设计中,我们可以通过以下手段来降低这种影响,优化天线性能。
(1)使用多点馈电的无源天线阵元。多点馈电能有效改善天线阵元的不圆度,减小因接收天线阵元引起的幅度差异。
(2)在抗干扰算法里针对各个通道进行相位补偿。人为地增加一个相位因子e-j(ψ-φm),将相位差异因子消除,此时公式(8)可以变为
wm(n+1)=wm(n)+2μambxm(n)e*(n)(10)
(3)设计增加辅助信道的增益。根据无源天线阵元的方向图不圆度情况来设计辅助信道的增益值,使得辅助通道总增益(天线+信道)总是大于主通道总增益值。
5 结束语
本文分析了通道幅相一致性对自适应算法的稳健性、收敛时间以及对天线阵列合成方向图的影响,并对其进行了仿真分析。最后针对系统中幅相不一致性的引起因素提出了改进措施,对工程设计有重要的指导作用。
随着现代电子技术的发展,干扰和反干扰技术逐渐成为了一个新的研究领域,而自适应调零天线作为系统的接收前端,是最有效的抗干扰措施。因此,对自适应调零天线工程化方面的研究有着重要的意义和价值。
[1]沈福民.自适应信号处理[M].西安:西安电子科技大学出版社,2001. SHEN Fu-min.Adaptive Signal Processing[M].Xi′an:Xidian University Press,2001.(in Chinese)
[2]徐建敏,华军.基于PI算法的GPS调零天线技术研究[J].通信对抗,2010(1):24-27. XU Jian-min,HUA Jun.Reasearch on GPS Adaptive Nulling Antenna Based on PIAlgorithm[J].Communication Countermeasures,2010(1):24-27.(in Chinese)
[3]石庆强,钟作伦,吴仁彪.基于LS-LMS的只能天线自适应抗干扰抑制方法[J].信号处理,2010,26(5):677-681. SHIQing-qiang,ZHONG Zuo-lun,WU Ren-biao. Smart Antenna Adaptive Interference Suppression Based on LS -LMSAlgorithm[J].Signal Processing,2010,26(5):677 -681.(in Chinese)
[4]高雪,胡鸿飞,傅德民.自适应天线阵中单元互耦对系统性能的影响[J].西安电子科技大学学报,2001,28(5):573-576. GAOXue,HUHong-fei,FUDe-min.The Effectof ElementMutual Coupling on the Performance of Adaptive Arrays[J].Journal of Xidian University,2001,28(5):573-576.(in Chinese)
[5]Fante R L,Vaccro J J.Wandband Cancellation of Interference in GPS Receive Array[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(2):549-564.
Analysis of Channels Inconsistence on Adaptive Nulling Antenna
HE Ling-yun
(Southwest China Institute of Electronic Technology,Chengdu 610036,China)
To inhance the anti-jamming performance of the adaptive nulling antennas system,the influence of channels inconsistent is analysed,including stability and convergency of the LMS algorithm.Some factors that can result in channels inconsistence are simulated and the results show that the imbalance of amplitudes and phases can worsen the function of the system.Finally,some effectivemeasures and design principles are provided in engineering application.
adaptive nulling antenna;anti-jamming;channels inconsistence;LMSalgorithm
the B.S.degree from Wuhan University in 2001.He isnow an engineer.His research concerns electromagnetic field and microwave.
1001-893X(2012)04-0548-05
2012-01-04;
2012-03-13
TN82
A
10.3969/j.issn.1001-893x.2012.04.025
何凌云(1980—),男,湖北潜江人,2001年于武汉大学获学士学位,现为工程师,主要研究方向为电磁场与微波。
Email:hely-tx@tom.com
HE Ling-yun was born in Qianjiang,Hubei Province,in 1980.He

