MLD结构下电磁兼容混响室内场均匀性分析

刘重阳，黄 华，张 行

（1.海装航订部，北京100841；2.船舶重工集团公司723所，扬州225001）

0 引 言

混响室作为当前主要的电磁兼容测试设备，越来越广泛地运用于辐射发射和辐射免疫性测试，以及封闭和屏蔽电缆的屏蔽效力等的测试。然而传统混响室的每次测试都是要伴随搅拌器足够多的步进数才能获得统计均匀的场，这样便使测试时间大大增加。如果采用散射体来代替搅拌器的作用，那么1次测试时间就仅是搅拌器步进1次的间歇时间，这样就在相当大的程度上缩短了测试时间，使得混响室更具有经济实用价值。因此，为了获得均匀的场而合理安排散射体在混响室中的位置就显得非常重要。

一般而言，几乎所有的混响室都是长方体的，利用模搅拌和模调谐来改变混响室内电磁场的边界条件，从而产生统计均匀分布的场［1］。国内外研究者在搅拌器的基础上提出了改变混响室的形状［2］、用散射体［3］以及散射体和搅 拌器相结合等方法［4－5］来优化混响室的性能。其中，混响室的形状可以改变成三角形和不对称的长方形；散射体类型最常用的有最大长度散射体（MLD）、施罗德二次剩余散射体（QRD）和原根剩余散射体（PRD）。

本文将从MLD的散射原理出发，具体给出它的设计步骤，最后分析了混响室内MLD不同位置下的场均匀性。

1 MLD散射原理与设计

1.1 MLD散射原理

散射体与相位反射栅的原理很相似，如图1所示。

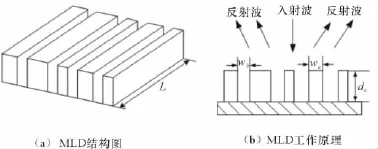
图1 MLD的结构和工作原理示意图

不同的阱深dn（n＝1，2，…）导致反射波与入射波的相位差为［6］：

式中：λ为电磁波在自由空间的波长。

实际上，散射体由在同一基准面上设置1组高度不同的长方体“脊”构成，习惯上，人们将长方体“脊”称为“阱”。散射体能够使混响室内某一区域的场成为统计均匀的原理如图1所示。具体说明如下：混响室内被关注区域（即企图使场为统计均匀的区域，一般在混响室的中部）任意一个点上的场，都是入射到散射体上的电磁波在散射体上各点产生的反射波的叠加，而由于散射体的反射面由1组宽度相同而深度不同的阱有序排列组成，因而来自于不同反射点而到达同一点后，各自相位是不同的（因各反射波的波程不同）。由于被关注区域内各点的场均由这样1组相位不同的反射波叠加而成，因而各点的场的统计效果相同。

本文采用MLD是因为它是上述3种散射体中结构形式最简单的。MLD结构依赖于一个伪随机序列，而且这一伪随机序列是伽罗瓦域（Galois Field）上1个数学群的基［7］。为了更好地对 MLD的设置过程予以理解，此处有必要对伽罗瓦域予以简单介绍。

伽罗瓦域是个有限域，通常用G（p）表示，其中p为质数且称之为该域的阶。有限域的一个重要性质是每个有限域G（p）至少要包含一个叫做α的本原元素，它能生成该域中的每个元素。实际中可以将G（p）延伸为一个含有pm个元素的域，这称为G（p）的扩展域，表示为G（pm），m 是一个非零的正整数。G（p）是G（pm）的子集。此处取p＝2，则G（2）为二进制域，除了数字0和1，在扩展域中还有本原元素α，则该域中的元素由｛0，1，α｝形成，根据文献［7］知扩展域G（2m）的元素由下面序列构成：

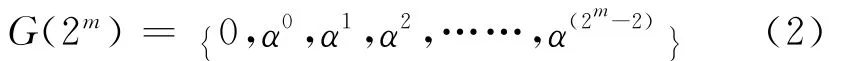
式中：该有限域中的元素个数为2m，非零元素个数为2m－1。

以G（24）［8］为例，即 m＝4，其编码规则如表1所示，其中α－power表示扩展域G（24）中元素α的指数，4－tuple表示与α－power相对应的4位二进制编码，从表中可知α15＝α0，这表明扩展域G（24）中仅有15个线性无关的非零元素，其它的非零元素可用这15个线性无关的非零元素构造而成，即αn＝

1.2 MLD结构设计

图1给出了MLD的结构和工作原理示意图。其中各参数的具体设置如下述：

在MLD结构中，所有阱的深度dn是一致的：

MLD结构中各个阱的宽度不同，其最大的阱宽度为：

表1 G（24）对应编码

而MLD中其余各阱宽wa则由伽罗瓦域上的基决定，在MLD阱宽wa确定后，MLD阱之间的距离wb也相应地被确定下来。

上面给出了MLD各个参数的约束条件，下面将给出工作频率范围为300MHz～2GHz、各散射体的总宽度相同（WT＝97.5cm）、长度一致（L＝100cm）的具体参数设计步骤：

（1）根据文献［8］可知，MLD的有限频率范围为1倍频，由于此处的上限频率为2GHz，故只需设计工作在1GHz频点上的MLD参数便可满足300MHz～2GHz频率范围要求。由于1GHz工作频率的波长λ0＝30cm，从而由前述方法可确定MLD阱的最大宽度wamax＝0.25λ0＝7.5cm；又由于总宽度WT已经确定为195cm，故在WT中所含编码的个数N＝WT／wamax＝26。

（2）根据前面对伽罗瓦域的介绍及表1可知，G（24）是采用4位二进制进行编码的，则每位编码所对应的阱宽 wn＝0.25×wamax＝0.25×7.5cm＝1.875cm。再由最大的阱宽度不能超过

0.25 λ0，即式（4）的约束条件可得，随机数的产生应满足一定要求，将其对应到G（24）编码上则要满足其不能同时出现5个1，即不能是11111，与之相对应的元素α的指数则满足如下8个约束条件：

（a）3后面不能为12；

（b）6后面不能为10、12；

（c）7后面不能为12；

（d）9后面不能为12；

（e）11后面不能为4、7、10、11、12；

（f）12后面不能为0、4、7、8、10、12、13；

（g）13后面不能为10、12；

（h）14后面不能为12。

（3）生成1组满足条件（1）和（2）的26个随机正整数，通过前面分析可知，所有的整数均可由G（24）中的15个线性无关的非零元素构成，则产生的这26个随机整数的编码可通过对15取模后再将其映射到伽罗瓦域G（24）编码上而得（表2给出了这么1组伪随机数及其对应的元素α的指数和编码），最后将这1组编码对应成MLD各个阱宽，现将该随机数编码下的MLD实际结构示意于图2。

图2 MLD实际结构

2 FDTD建模

在此，以尺寸7.6m×5.2m×3.3m的混响室为例进行仿真分析。图3为仿真计算中的3种类型混响室的结构示意图：图3（a）为装有搅拌器的混响室结构示意图；图3（b）为在6个壁面上设置有散射体的混响室的结构示意图；图3（c）为在8个顶角上均设置有散射体的混响室结构示意图。

本文采用时域有限差分（FDTD）方法对混响室内的场进行仿真分析。为了获得较高的计算精度，网格大小取为Δx＝Δy＝Δz＝2.5cm；同时，为了满足数值稳定性的要求，时间步长取为Δt＝4.81×10－11s；为使场达到稳定，所选取的总时间步数则根据散射体及其所处的位置而定。混响室壁和散射体选用相同的良导体材料，其电导率σ＝9×106S／m，相对介电常数εr＝1.0，混响室腔壁厚1cm。分析时采用完美匹配层吸收边界条件（UPML），计算区域沿x、y、z方向的网格数为324×228×152，其中，每个方向上包括10个网格厚度吸收边界层；在预设精度下的均匀区的尺寸为100Δx×148Δy×72Δz。波源辐射出正弦平面电磁波，其幅值为1V／m，波源的位置设置在点（44，44，50）处。

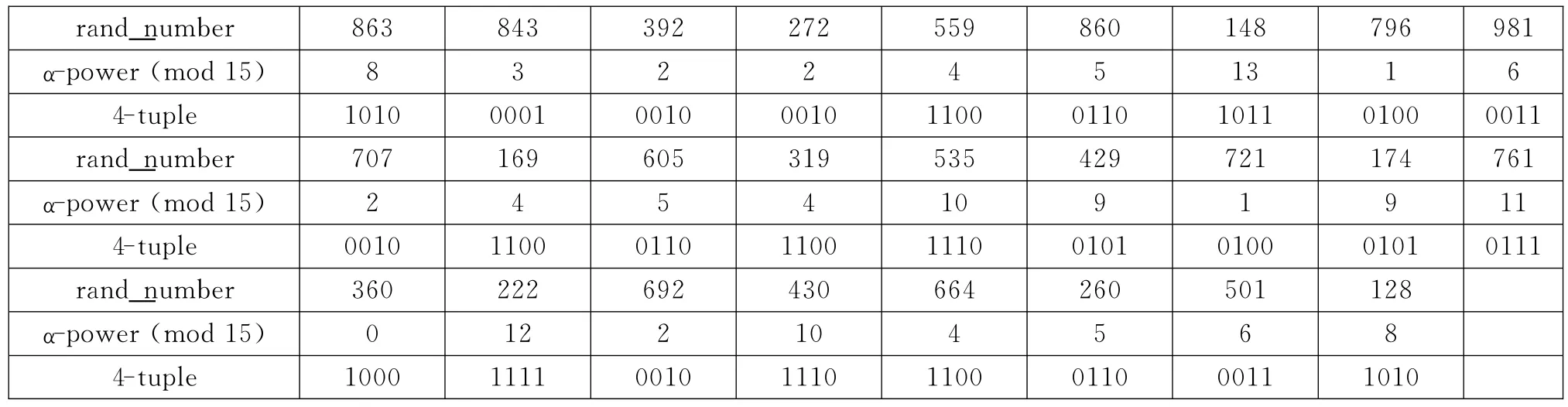
表2 满足条件的1组伪随机数及其G（24）编码

3 仿真计算及结果分析

为了进行对比性实验，分析了f＝915MHz，以下3种情况时混响室内场的特性（如图3所示）：情况1，只设置有搅拌器的混响室；情况2，散射体位于混响室的6个面上；情况3，散射体位于混响室的8个角落处。

3.1 电场强度的归一化标准偏差

仿真分析中计算了3种情况下混响室内8个点处的电场强度Ex、Ey、Ez和｜E｜的值，这8个点为：（1）（0.75m，0.75m，0.75m）；（2）（0.75m，4.475m，0.75m）；（3）（0.75m，0.75m，2.55m）；（4）（0.75m，4.475m，2.55m）；（5）（3.25m，0.75m，0.75m）；（6）（3.25m，4.475m，0.75m）；（7）（3.25m，0.75m，2.55m）；（8）（3.25m，4.475m，2.55m）。这8个点是依据IEC61000－4－21测试标准要求选取的，其中，每2个点相距0.4m，且离地面有0.7m的距离。归一化标准偏差如表3所示。从表中可以看出在只设置有搅拌器情况下混响室内的归一化标准偏差略小于IEC61000－4－21标准所规定的3dB要求，亦即表明其内部场均匀满足标准要求；散射体位于6个面和8个角落处时，混响室内部的场都是均匀的，且散射体位于8个角落时混响室内的场比散射体位于6个面时混响室内场的均匀性要好。

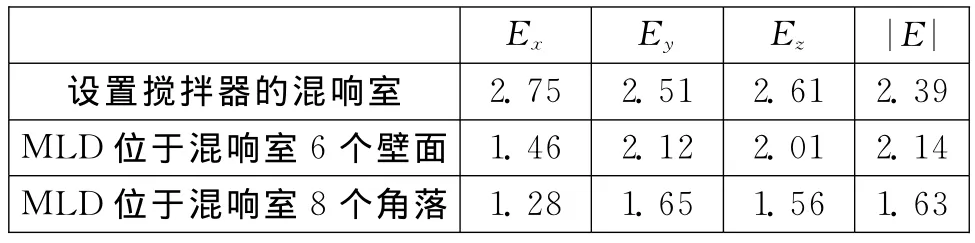
表3 混响室内电场强度的归一化标准偏差σ（dB）

3.2 电场强度的累积概率分布

电场强度Ex、Ey和Ez3个分量的累积概率分布函数（CDF）如图4所示。所分析计算的这3种情况下的混响室的内部空间都是一致的，均为7.6m×5.2m×3.3m，且电场强度Ex、Ey和Ez3个分量的值取的都是z＝82时平面x－y内的值。从图中可以明显看出，图4（b）与图4（c）中Ex、Ey和Ez的CDF曲线更接近理论值，说明其均匀性比图4（a）好，图4（c）的CDF比图4（b）的均匀性要稍微好一点。这就表明本文所设置散射体的位置可引起更均匀的场分布，且比文献［2］中的场均匀性要好。

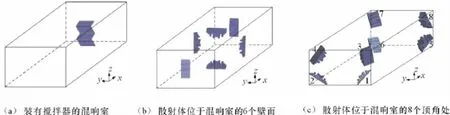
图3 仿真计算中3种类型混响室的结构图

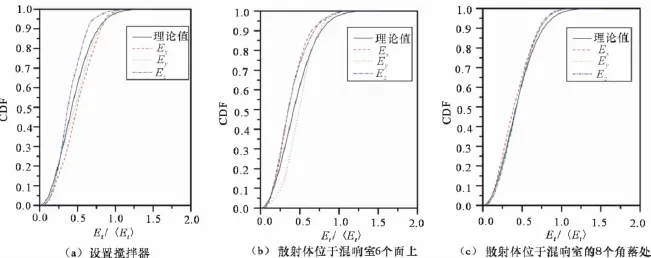
图4 电场强度的累积概率分布

4 结束语

本文提出了混响室中MLD散射体的一种新的位置，并采用FDTD对其所产生的场均匀性进行了仿真分析，将其与设置搅拌器的混响室以及文献［2］中的散射体位于混响室的6个面的场均匀性进行了对比，验证了该位置的可行性。散射体放置于混响室的角落处不仅有效提高了混响室中的场均匀性，还大大减少了利用混响室进行测试的时间，从而为混响室的设计和测试提供了可靠的理论指导。

［1］IEC－61000－4－21，Testing and Measurement Techniques Reverberation Chamber Testethods［S］.

［2］Rhee J G.Field uniformity characteristics of an asymmetric structure reverberation chamber by FDTD method［A］.Asia－Pacific Conference on Environmental Electromagnetics［C］，2003：426－429.

［3］Amaut L R.Operation of electromagnetic reverberation chambers with wave diffractors at relatively low frequencies［J］.IEEE Transactions on Electromagnetic Compatibility，2001，43（4）：637－653.

［4］Petisch M，Schwab J S.Investigation of the field uniformity of a mode－stirred chamber using diffusors based on acoustic theory［J］.IEEE Transactions on E－lectromagnetic Compatibility，1999，41（4）：446－451.

［5］何鹏，蒋全兴，周香，等.声学散射体对混波室场均匀性的影响［J］.微波学报，2009，25（2）：38－41.

［6］Antred M，Chroeder R S.Progressin architectural acoustics and artificial reverberation：concert hall acousticsand number theory［J］.Journal of The Audio Engineer Society，1984，32（4）：94－203.

［7］Petirsch M，Schwab A J.Investigation of the field uniformity of a mode－stirred chamber using diffusers based on acoustic theory［J］.IEEE Transactions on E－lectromagnetic Compatibility，1999，41（4）：446－451.

［8］Schroeder M R.Number Theory in Science and Communication［M］.Berlin，Germany：Springer－Verlag，1944.