考虑蠕变效应的岩石损伤起始准则
卞跃威,夏才初,肖维民,朱合华
(同济大学a.岩土及地下工程教育部重点实验室;b.土木工程学院地下建筑与工程系,上海 200092)
1 研究背景
地下工程施工中发生的大变形、突然坍塌,以及已竣工的地下结构经历一定的时间后发生的失稳破坏,推进了岩石蠕变和损伤特性的研究工作[1-7]。包含损伤因子的本构方程,能够描述岩石等脆性材料的第 3 阶段蠕变(加速蠕变段)[8-15]。
损伤的发展包括损伤因子变化历程和损伤起始点2个方面。损伤的变化历程取决于损伤因子的定义[5],将损伤因子对于时间求导便可得到相应的损伤变化量;单纯从材料的蠕变曲线观察,损伤的起始点是定常蠕变之末[16],但是对于某一类特定的岩石材料而言,如需要将这一现象的认识表示成材料应力、应变的数学表达式,其基本的思路同岩石材料中塑性屈服面的定义。Chan等人认为共轭应力功的度量值大于零时,为岩石材料的损伤起始点[9];Aubertin&Simon[17]则依据岩石材料的屈服准则,假定当应力水平达到一定程度时为损伤的起始点[17]。这2种损伤起始准则都认为岩石损伤的起始取决于其内部的应力状态,它们在应力空间中为一固定的曲面。而岩石损伤的诱发和发展机制为应力的增加或变形的累积导致材料中的微裂隙和微缺陷的出现和发展[6],所以,即使岩石的应力状态处于Chan和Aubertin&Simon所定义的损伤起始面以下时,也可能会由于蠕变应变的累积,使得材料产生损伤而进入加速蠕变阶段,并最终破坏。
本文在Drucker-Prager屈服准则[18]的基础之上,结合Aubertin&Simon关于岩石损伤起始点的定义[17],并且考虑蠕变应变的影响,定义了岩石损伤起始准则。该准则为应力、塑性变形和蠕变变形的函数;并且假定瞬时塑性变形只引起岩石材料的塑性硬化,而蠕变变形只引起岩石的软化。这在应力空间中主要表现为随着蠕变应变的增加损伤起始面逐渐缩小,其极限情况是与岩石的初始屈服面重合。这种现象与岩石等脆性材料的蠕变试验结果是一致的。
2 考虑蠕变的损伤起始准则
确定岩石的损伤起始准则需要对同一种岩石进行多个不同应力水平的蠕变试验直至岩石试件破坏。当应力水平较低时,需要较长的时间试件才能达到损伤起始点,所以这样的试验需要浪费大量的时间,但是如果选择较大的应力水平时,往往在加载的过程中就会发生瞬时破坏,很难得到岩石试样的全过程蠕变曲线。Bieniawski[19]曾经采用常应变率单轴压缩试验研究砂岩的蠕变特性,试验中轴向应变速率分别为

试验表明:岩石的单轴抗压强度随着应变速率的增加而增加,而残余强度则随着应变速率的增加而减小,并且达到峰值强度之时所对应岩石总的轴向应变也随着应变率的增加而减少(见图1)。由于岩石的轴向蠕变应变可表示为其中:εtotal为总的应变,相当于图1中的 εaxial;εe为弹性应变,随着应力增大而增加;εp为瞬时塑性应变,随着应力梯度增大而增加。图1所示的单轴压缩试验中,随着应变率的增加,峰值强度增加,并且,峰值应力点处总应变减小,瞬时塑性应变增加,弹性变形也增加,因而由前面式子可知:随着应变率的增加,蠕变应变εc会减小。从而可见考虑蠕变应变后,岩石的强度会有所下降,即岩石表现出蠕变软化特性,这种特性也可以通过碳质板岩的多级加载单轴压缩蠕变试验得到验证,见图2。
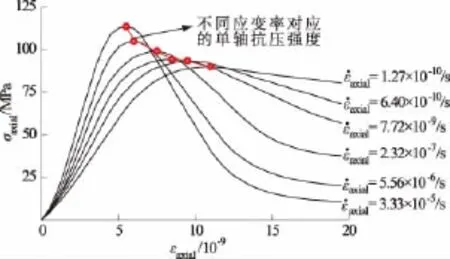
图1 砂岩单轴压缩试验全应力-应变曲线[19]Fig.1 Stress-strain curves obtained from uniaxial compressive tests on sandstone[19]

图2 碳质板岩单轴压缩试验应力-应变曲线Fig.2 Stress-strain curves obtained from uniaxial creep tests on carbonaceous slate
多级加载单轴压缩蠕变试验中,可以得到图2所示的全应力-应变曲线,其中OA为加载过程中瞬时应力-应变曲线,而OB为加载到某一应力水平并经历一段时间,产生蠕变变形后,总的应力-应变曲线。当轴向应力瞬时增加到38.3 MPa(图2中A点)时,对应的瞬时应变为3.82×10-2,岩石并没有出现破坏的迹象,则可以推测瞬时加载情况下,岩石强度应该大于A点的应力水平,所以A点以后的应力-应变关系会沿着图2中所示的箭头发展。保持载荷恒定,经过一段时间(约为59 min),产生的轴向蠕变应变为8.6×10-3,对应的总应变为4.68×10-2(图2中B点),试件破坏,破坏以后岩石失去承载能力,所以B点以后岩石的应力-应变关系会沿着B处的箭头所示方向发展。考虑蠕变以后,岩石的单轴抗压强度明显低于瞬时抗压强度,其原因在于蠕变对岩石材料的劣化作用。劣化的机制是受力过程中岩石内部的微裂纹成核并发展[5],即岩石内部损伤的启动和发展。
在恒定载荷作用下,蠕变变形累积效应达到一定量值,即损伤起始点,则微裂纹扩展和贯通,岩石的有效承载面积会减小,从而内部真实应力增加更进一步加速材料的劣化。图3为一组红砂岩在恒定应力水平下的蠕变破坏试验,在应力水平较低时,σaxial=52.8 MPa,试样经过较长的时间 (t=12.67 h),才出现加速蠕变段,此时对应的轴向蠕变应变为5.31 ×10-4;在较高应力水平,σaxial=58.31 MPa,试样达到第三蠕变阶段所需要的时间较短(t=2.83 h),相应的蠕变应变值为5.13 ×10-4。所以,损伤起始点与应力水平和蠕变应变绝对量值的大小有一定的关系,如图3(b)所示。这与前面Bieniawski实验分析结果基本是一致的。
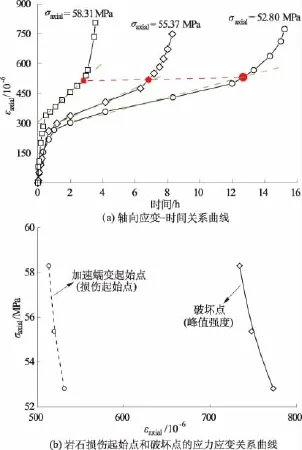
图3 红砂岩蠕变损伤及破坏(单轴抗压强度为80 MPa)Fig.3 Creep damage and rupture of red sandstone(under 80 MPa uniaxial strength)
Aubertin& Simon[17]根据岩石全应力应变曲线总结出岩石损伤的起始准则,认为岩石损伤的起始点介于初始屈服和最终破坏点之间,通常约为岩石单轴抗压强度的50%~90%,在应力空间中损伤起始面为介于初始屈服面和破坏面之间的与破坏面相似的曲面,只取决于所承受的应力水平,与岩石的变形无关。基于这一认识,Aubertin&Simon提出了由应力分量构成的损伤起始准则[17],准则的形式与岩石的破坏准则[20]相同,只是将破坏准则中代表岩石单轴抗压和抗拉强度的参数σc和σt替换为损伤起始时刻围岩的单轴压应力σcd和拉应力σtd。
如果围岩的破坏遵循 Drucker-Prager准则[19],即
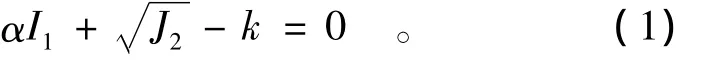
其中:

式中:取压应力为正值;σe为等效应力;σm为平均应力;σii为主应力张量之和;Sij为偏应力张量,Sij=σij- δijσm;σij为应力张量;δij为克罗内克尔记号;α,k为岩石参数。
参数k取决于材料的应力状态,例如[21]:
当材料受单轴压力时,
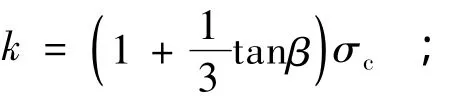
当材料受单轴拉力时,
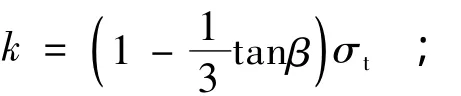
当材料受纯剪应力时,

式中:σc,σt,τf分别为岩石的单轴抗压强度、单轴抗拉强度和抗剪强度。
综合以上各式,可将k表示为更为一般的形式,

式中:σf为破坏点处对应的第二偏应力不变量的平方根。
按照 Aubertin& Simon[17]的方法,可以将式(1)中的参数k替换为损伤起始时刻对应的kd,并且将I1,J2代换为σm和σe,从而得到损伤起始准则在σm-σe平面内的表达式为
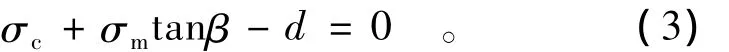
其中:
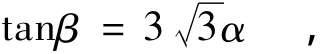
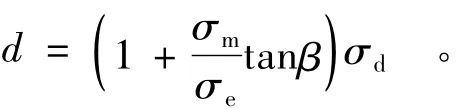
式中:β为损伤起始准则在σm-σe平面上所形成的曲线与σm轴的夹角;d为损伤起始准则在σe轴上的截距;σd为损伤起始时刻对应的等效应力。
式(3)为不考虑蠕变应变软化时的岩石损伤起始准则,损伤起始点介于初始屈服面与破坏面之间。因此,损伤产生以前的材料服从塑性硬化准则,瞬时塑性应变的增加使得岩石内部产生晶格位错[22];损伤开始以后,岩石内部出现沿着最大主应力方向开展的裂纹[23],如果存在瞬时塑性应变,则损伤和硬化现象同时存在,达到峰值强度时,岩石内部微裂纹贯通并且凝聚成核[24],则硬化作用已经消失,损伤起主导作用,材料强度逐渐降低。
根据Ludwik方程所描述的关系[25-26]可以将式(3)中的等效应力σd表示为初始屈服时刻的等效应力和等效瞬时塑性应变的函数,假定当等效瞬时塑性应变达到时,开始出现损伤,那么

岩石的破坏准则与蠕变应变相关性已经为众多的研究者所证实[27-31]。由前面分析表明损伤起始准则与岩石的蠕变应变也存在着类似的相关性——随着蠕变应变的增加,损伤起始应力逐渐减小。试验观测表明:材料的损伤起始应力可能与蠕变应变速率成线性关系[30],也可能与材料的蠕变应变呈某对应关系,即:ξ= ξ(),其中ξ为与蠕变变形有关的软化参数[29],为蠕变应变张量。基于以下几点,本文亦采用Ludwik方程描述岩石的蠕变应变软化特性:①瞬时塑性应变硬化和蠕变应变软化公式形式上一致,利于数学处理;②根据图3(b)损伤应力与应变之间的关系可知损伤起始应力随着蠕变应变的增加呈现非线性衰减趋势。因而

将式(4)代入式(5)得到

综合式(3)至式(6),可以得到考虑蠕变效应的损伤起始准则为
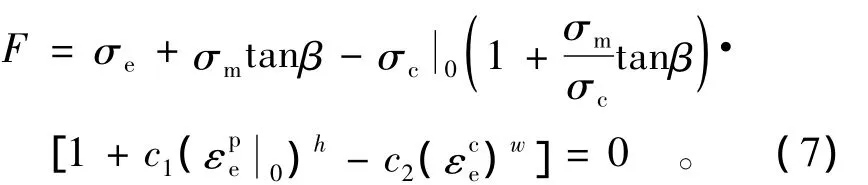
式(7)所表示的损伤起始准则在π平面上形成的曲面为介于初始屈服面与破坏面之间的随着蠕变应变增加而收缩的同心圆。如图4所示,其中损伤起始面所组成的同心圆半径为
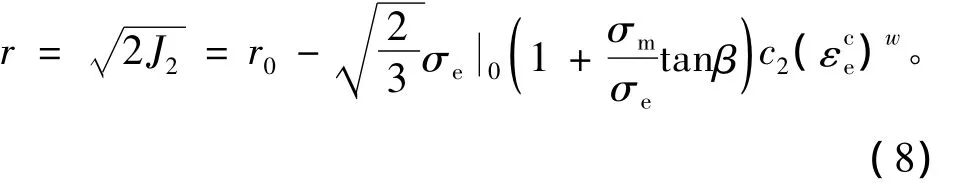
其中:


图4 损伤起始面在π平面上的曲线Fig.4 Damage initiation surface on the deviator stress plane
应力空间中,损伤起始面可以通过以下2种试验方案确定:①对同一类岩石进行至少一组(包含3个试样)压缩试验,并且每个试样的围压都不相同,然后再做至少一组蠕变破坏试验(包含3个试样);②采用Fossum提出的多阶段试验方案[32],对一个试样进行不同围压的加卸载试验(至少包含3种不同围压),然后再至少做一组蠕变破坏试验(包含3个试样)。
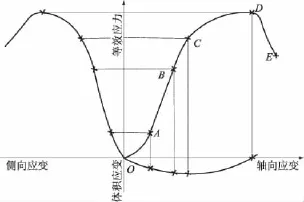
图5 岩石压缩试验全过程应力-应变曲线[17]Fig.5 Stress-strain curves obtained from compressive tests on rocks[17]
3 分析与试验验证
由公式(7)确定的损伤起始面在σm-σe平面上为一系列平行于破坏面和屈服面的曲线,如图6所示,蠕变效应使得损伤起始面与σe轴的截距呈现减小的趋势,这与Reiner(1960)关于蠕变应变对屈服面的影响研究结果[27]是相似的。

图6 σm-σe平面内的损伤起始面Fig.6 Damage initiation surface in σm-σeplane
准则假定岩石在拉伸应力作用下的损伤特性与压缩时是一致的,而实际的拉伸试验表明:在拉伸情况下,一旦岩石内部出现微小的缺相或裂隙,则迅速破坏[12,23,33],在单轴拉伸的情况下,岩石的损伤起始点与岩石的初始屈服点基本上是同一个应力水平σT 0[34-35],而压缩时损伤并非在初始屈服点处。所以,与屈服准则相类似引入拉伸屈服强度和压缩屈服强度比值ω,可以将式(7)中的σe替换为应力组合形式 t[21]:
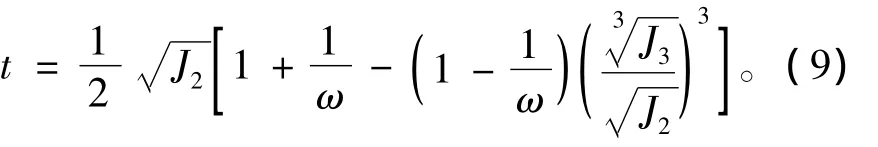
式中:J3为第三偏应力不变量。
再将式(7)中的σm替换为I1,可以得到

式中:t0为初始屈服时刻材料内的应力组合t的值。
当不考虑蠕变对材料的劣化效应,即c2=0,那么损伤起始准则退化为式(3),c2≥0的限制条件保证了应力空间中损伤起始面总是位于塑性屈服面之下,这点符合试验观察结果。
如果忽略压缩试验中材料的塑性硬化特性,则材料的初始屈服应力和峰值强度相同,那么公式(5)中的瞬时损伤起始点与材料的峰值强度时对应的等效应力相等,即

将式(11)代入式(7)得到:

同样可以采用式(7)表示受压时岩石的损伤起始准则。

单轴受力状态下,σ3=0,式(12)简化为式(13)两边同时约去1-tanβ/3,则反映单轴压缩情况下损伤起始应力随着蠕变应变的增加而减小的趋势。

例如,红砂岩的单轴压缩试验,由瞬时加载试验得到单轴抗压强度为σCU=80 MPa。即等效蠕变应变=0损伤起始应力为σ1=80 MPa。另外再进行5次蠕变试验得到等效蠕变应变与损伤起始应力,见表1。

表1 单轴压缩试验中蠕变应变及考虑蠕变效应的损伤起始应力Table 1 Creep strains and corresponding initial stresses of damage in uniaxial compressive creep tests
用式(13)拟合上表等效蠕变应变及其对应的损伤起始应力得到:c2=3.49 ×1021,ω =6.42。理论值和实测值的峰值应力随蠕变应变的发展规律见图7,可见理论公式能够和试验的实测值较好地吻合。

图7 红砂岩损伤起始点和蠕变应变关系(试验和理论计算结果)Fig.7 Relationship between damage initiation and creep strain of red sandstone(test and theoretical results)
4 结论
结合Aubertin& Simon[17]损伤起始点的定义,在Drucker-Prager准则的基础上提出了岩石损伤起始准则。该准则主要有以下特点:
(1)充分考虑了蠕变对岩石损伤的的影响,与不考虑蠕变效应的单纯应力表示的损伤起始准则相比,更加合理。
(2)采用Ludwik方程描述岩石损伤起始面与蠕变应变的关系,能够很好地解释蠕变破坏试验中岩石损伤起始应力随着蠕变应变增加而非线性减小的现象。
(3)依据该损伤起始准则,岩石即使在常应力作用下,蠕变量的增加也会导致损伤发展;应力水平越高则达到损伤起始点需要的时间越少,相应的蠕变应变量也越小;应力水平低则达到损伤起始点所需要的时间越长,对应的蠕变应变量较大。(4)损伤起始准则中包含的材料参数可以通过常规三轴试验和单轴蠕变试验很方便地加以确定。
[1]KACHANOV L.Rupture Time under Creep Conditions[J].International Journal of Fracture,1999,97(1 -4):11-18.
[2]谢和平.岩石、混凝土损伤力学[M].徐州:中国矿业大学出版社,1990.(XIE He-ping.Damage Mechanics of Rocks and Concrete[M].Xuzhou:The Publishing House of China University of Mining and Technology,1990.(in Chinese))
[3]DOUGILL J,LAU J,BURT N.Towards a Theoretical Model for Progressive Failure and Softening in Rock,Concrete and Similar Materials[C]∥Mechanics in Engineering.Virginia:American Society of Civil Engineers ASCE Press,1976:335 -355.
[4]DRAGON A,MROZ Z.A Model for Plastic Creep of Rock-Like Materials Accounting for the Kinetics of Fracture[J].International Journal of Rock Mechanics and Mining Sciences& Geomechanics Abstracts,1979,16(4):253-259.
[5]LEMAITRE J,DUFAILLY J.Damage Measurements[J].Engineering Fracture Mechanics,1987,28(5 -6):643-661.
[6]COSTIN L.Time Dependent Deformation and Failure:Chapter 5 in Fracture Mechanics of Rock(Atkinson Edition)[M].London:Academic Press Inc.,1987.
[7]BODNER S,CHAN K.Modeling of Continuum Damage for Application in Elastic-Viscoplastic Constitutive Equations[J].Engineering Fracture Mechanics,1986,25(5-6):705-712.
[8]LECKIE F,HAYHURST D.Constitutive Equations for Creep Rupture[J].ACTA Metallurgica,1977,25(9):1059-1070.
[9]CHAN K,BODNER S,FOSSUM A,et al.A Constitutive Model for Inelastic Flow and Damage Evolution in Solids under Triaxial Compression[J].Mechanics of Materials,1992,14(1):1-14.
[10]DUSSEAULT M,FORDHAM C.Time Dependent Behaviour of Rocks[M].Oxford:Pergamon Press,1993.
[11]LOCKNER D.A Generalized Law for Brittle Deformation of Westerly Granite[J].Journal of Geophysical Research,1998,103(B3):5107-5123.
[12]MAIN G.A Damage Mechanics Model for Power-law Creep and Earthquake Aftershock and Foreshock Sequences[J].Geophysical Journal International,2000,142(1):151-161.
[13]杨春和,陈 锋,曾义金.盐岩蠕变损伤关系研究[J].岩石力学与工程学报,2002,21(17):1602-1604.(YANG Chun-he,CHEN Feng,ZENG Yi-jin.Investigation on Creep Damage Constitutive Theory of Salt Rock[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(17),1602 -1604.(in Chinese))
[14]朱昌星,阮怀宁,朱珍德,等.岩石非线性蠕变损伤模型的研究[J].岩土工程学报,2008,30(10):1510-1513.(ZHU Chang-xing,RUAN Huai-ning,ZHU zhende,et al.Non-linear Rheological Damage Model of Rock[J].Chinese Journal of Geotechnical Engineering,2008,30(10):1510 -1513.(in Chinese))
[15]HEAP M,BAUD P,MEREDITH P,et al.Time-dependent Brittle Creep in Darley Dale Sandstone[J].Journal of Geophysical Research,2009,114(B07203):1-22.
[16]金丰年,范华林,蒲奎源.岩石蠕变损伤模型研究[J].工程力学,2000,(增):227 -331.(JIN Feng-nian,FAN Hua-lin,PU Kui-yuan.Investigation on Creep Damage Model[J]. Engineering Mechanics,2000,(Sup.):227 -331.(in Chinese))
[17]AUBERTIN M,SIMON R.A Damage Initiation Criterion for Low Porosity Rocks[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(3 -4):554-554.
[18]DRUCKER D C,PRAGER W.Soil Mechanics and Plastic Analysis or Limit Design[J].Quarterly of Applied Mathematics,1952,10(2):147 -165.
[19]BIENIAWSKI Z.Time-Dependent Behaviour of Fractured Rock[J].Rock Mechanics,1970,2(3):123 -137.
[20]AUBERTIN M,SIMON R.A Multiaxial Failure Criterion That Combines Two Quadric Surfaces[C]∥American Rock Mechanics Association.Proceedings of the 2nd North American Rock Mechanics Symposium.Montreal,Quebec,Canada,June 19-21,1996:1729-1736.
[21]Hibbit,Kalsson,and Sorenson,Inc..Abaqus User’s Manual 6.9[K].Pawtucket,Rhode Island:Hibbit,Kalsson,and Sorenson,Inc.,2010.
[22]MUNSON D.Preliminary Deformation Mechanism Map for Salt(with Application to WIPP)[R].Albuquerque,New Mexico,USA:Sandia National Laboratories,1979.
[23]MOGI K.Flow and Fracture of Rocks under General Triaxial Compression[J].Applied Mathematics and Mechanics(English Edition),1981,2(6):635-651.
[24]KACHANOV M.Elastic Solids with Many Cracks and Related Problems[J].Advances in Applied Mechanics,1993,30:259-445.
[25]ONO K.Strain-Hardening Equations and Uniform Strain[J].Metallurgical and Materials Transactions B,1972,3(3):749-751.
[26]SODERBERG A,SELLGREN U.Modelling of Strain Hardening and Strain Rate Hardening of Dual Phase Steels in Finite Element Analysis of Energy-Absorbing Components[C]∥National Agency for Finite Element Methodsand Standards.NAFEMS World Congress(2005),Malta,May 17 -20,2005.
[27]REINER M.Plastic Yielding in Anelasticity[J].Journal of the Mechanics and Physics of Solids,1960,8:255 -261.
[28]NAGHDI P,MURCH S.On the Mechanical Behaviour of on the Viscoelastic-Plastic Solids[J].Journal of Applied Mechanics,September,1963,30:321 -328.
[29]PERZYNA P.Fundamental Problems in Viscoplasticity[J].Advances in Applied Mechanics,1966,9:243 -377.
[30]MROZ Z,ANGELILLO M.Rate Dependent Degradation Model for Concrete and Rock[C]∥Swiss Federal Institute of Technology.Proceeding of International Conference on Numerical Model in Geomechanics,Sept 13-17,1982,Zurich:A.A.Balkema Publishers,1982:208-217.
[31]KUCHARSKI S,MROZA Z.Identification of Yield Stress and Plastic Hardening Parameters from a Spherical Indentation Test[J].International Journal of Mechanical Sciences,2007,49(11):1238-1250.
[32]FOSSUM A,FREDRICH J.Estimation of Constitutive Parameters for the Belridge Diatomite South Belridge Diatomite Field[R].Albuquerque,New Mexico,USA:Sandia National Laboratories,1998.
[33]COCKS A,ASHBY M.On Creep Fracture by Void Growth[J].Progress in Materials Science,1982,27(3-4):189-244.
[34]THEOCARIS P.Failure Criteria for Isotropic Bodies Revisited[J].Engineering Fracture Mechanics,1995,51(2):239-264.
[35]DEBERNARDI D,BARLA G.New Viscoplastic Model for Design Analysis of Tunnels in Squeezing Conditions[J].Rock Mechanics and Rock Engineering,2009,42(2):259-288.

